ЗНО онлайн 2016 року з фізики – додаткова сесія

ТЕМА: Механіка. Основи кінематики. Нерівномірний рух. Середня і миттєва швидкості.

Завдання скеровано на перевірку розуміння фізичного змісту середньої швидкості.

Середня швидкість \(v_\text{сер}\) дорівнює відношенню всього шляху \(l\) до інтервалу часу \(t,\) за який цей шлях подолано:

Перша частина шляху \(l_1=900\ \text{м}\), її велосипедист подолав зі швидкістю \(v_1=15\ \text{м/с.}\) Обчислімо час $$ t_1=\frac{l_1}{v_1}=\frac{900\ \text{м}}{15\ \text{м/с}}=60\ \text{с.} $$

Друга частина шляху \(l_2=400\ \text{м}.\) Її велосипедист подолав зі швидкістю \(v_2=36\ \text{км/год}=10\ \text{м/с}.\) Обчислимо час

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Вага тіла.

Завдання скеровано на перевірку розуміння сили, яку називають вагою.

Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають \(\overrightarrow{P}.\)

Вантаж і нижній динамометр підвішені до верхнього динамометра й розтягують його пружину. Отже, верхній динамометр покаже загальну вагу вантажа та нижнього динамометра: \begin{gather*} P=P_\text{вантажа}+P_\text{динамометра},\\[7pt] P=120\ \text{Н}+10\ \text{Н}=130\ \text{Н}. \end{gather*}

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку вміння визначати кінематичні характеристики (швидкість руху) під час вільного падіння.

Спосіб 1. Для визначення швидкості руху м᾽яча на певній висоті скористаймося кінематичним рівнянням, яким описують вільне падіння вздовж вертикальної осі \(Oy:\) $$ \Delta h=\frac{v^2-v^2_0}{2g}, $$ де \(\Delta h\) ‒ різниця висот, яку пройшов м᾽яч \((\Delta h=30-3=27\ \text{м}),\ v\) ‒ шукана швидкість руху на висоті \(3\ \text{м},\) \(v_0\) ‒ початкова швидкість, із якою кинули м᾽яч із висоти \(30\ \text{м},\ g\) ‒ прискорення вільного падіння:

Спосіб 2. Для визначення швидкості руху м᾽яча на певній висоті можна також скористатися законом збереження механічної енергії: сума потенціальної і кінетичної енергій на висоті \(h=30\ \text{м}\) дорівнює сумі потенціальної і кінетичної енергій на висоті \(h_1=3\ \text{м}:\)

Відповідь: Б.

ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.

Завдання скеровано на перевірку вміння розв᾽язувати задачі, коли на тіло діє кілька сил.

Позначмо сили, які діють на тіло, занурене в олію, а потім – у воду.

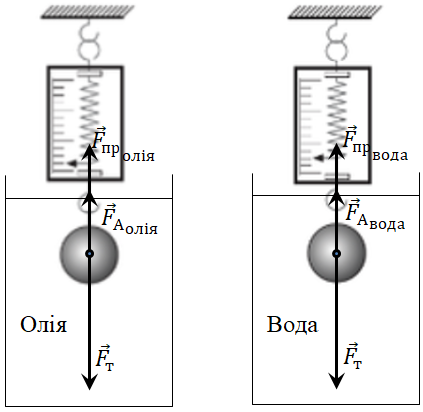
Запишімо рівняння другого закону Ньютона в проєкціях на вертикальну вісь, напрямлену вниз: $$ \left\{ \begin{array}{l} F_\text{т}=F_{\text{пр}_\text{олія}}+F_{\text{A}_\text{олія}}\\ F_\text{т}=F_{\text{пр}_\text{вода}}+F_{\text{A}_\text{вода}}, \end{array}\right. $$ де \(F_\text{т}\) ‒ сила тяжіння, що не залежить від рідини, у яку занурено тіло, \(F_{\text{пр}_\text{олія}}\) і \(F_{\text{пр}_\text{вода}}\) ‒ сили пружності, \(F_{\text{A}_\text{олія}}\) і \(F_{\text{A}_\text{вода}}\) ‒ сили Архімеда.

Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають \(\overrightarrow{P}.\) Отже, за третім законом Ньютона \(F_\text{пр}=P.\) $$ \left\{ \begin{array}{l} F_\text{т}=P_{\text{олія}}+F_{\text{A}_\text{олія}}\\ F_\text{т}=P_{\text{вода}}+F_{\text{A}_\text{вода}}, \end{array}\right. $$

Прирівняємо праві частини цих формул: \begin{gather*} P_{\text{олія}}+F_{\text{A}_\text{олія}}=P_{\text{вода}}+F_{\text{A}_\text{вода}},\\[7pt] P_{\text{олія}}-P_{\text{вода}}=F_{\text{A}_\text{вода}}-F_{\text{A}_\text{олія}},\\[7pt] \Delta P=F_{\text{A}_\text{вода}}-F_{\text{A}_\text{олія}}, \end{gather*} де \(\Delta P\) ‒ це та різниця у вазі, яку показав динамометр під час зважування у воді й олії.

Запишімо, чому дорівнює сила Архімеда у воді та олії: \begin{gather*} \Delta P=\mathbf{\rho}_\text{вода}gV_\text{т}-\mathbf{\rho}_\text{олія}gV_\text{т}, \end{gather*} де \(\mathbf{\rho}_\text{вода}\) і \(\mathbf{\rho}_\text{олія}\) ‒ густини, \(g\) ‒ прискорення вільного падіння, \(V_\text{т}\) ‒ шуканий об᾽єм тіла.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та дослідне обґрунтування їх.

Завдання скеровано на перевірку знання базових понять молекулярної фізики й розуміння процесів, описаних за допомогою цих понять.

Теплопровідність ‒ це вид теплопередачі, зумовлений хаотичним рухом і взаємодією частинок речовини без перенесення її.

Хімічна реакція ‒ це перетворення речовин, під час якого з одних речовин утворюються інші.

Конвекція ‒ це вид теплопередачі, під час якого теплоту переносять потоки рідини або газу.

Дифузія ‒ це взаємне проникнення структурних частинок (молекул, атомів, йонів) однієї речовини між структурними частинками іншої внаслідок їхнього теплового руху.

Помідор у солоній воді не нагріється і нові речовини не утворяться. А от солоним він стане, тобто йони солі проникнуть у помідор унаслідок безперервного теплового руху, отже, відбудеться дифузія.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=const, $$ де \(p\) ‒ тиск, \(V\) ‒ об’єм, \(T\) ‒ абсолютна температура.

Графік 1 відповідає ізохорному охолодженню (\(V=const\) ‒ графік паралельний осі абсолютної температури, температура \(T\) під час цього знижується).

Графік 3 відповідає ізотермічному стисканню (\(T=const\) ‒ графік паралельний осі об’єму, під час цього об’єм зменшується).

Під час процесів 2 і 4 змінюються і об’єм, і температура. Під час процесу 4 хоча температура й знижується, але об’єм збільшується, тому тиск також знижуватиметься. Отже, цей процес не може бути ізобарним.

Графік 2 відповідає ізобарному охолодженню (об’єм зменшується пропорційно до зниження температури, отже, \(p=const\)).

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння роботи в термодинаміці.

Робота газу виконуватиметься, якщо змінюватиметься його об᾽єм. Якщо об’єм газу збільшується, то газ виконує додатну роботу. Якщо об’єм газу зменшується, то робота газу від’ємна.

Під час ізобарного процесу роботу \(A\) газу можна визначити за формулою $$ A=p\Delta V, $$ де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об᾽єму.

З іншого боку скористаємося рівнянням стану ідеального газу (рівнянням Менделєєва ‒ Клапейрона): $$ p\Delta V=\frac mM R\Delta T, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, роботу, яку виконує розріджений азот, можна визначити за формулою

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря і вимірювання її.

Завдання скеровано на перевірку розуміння відносної вологості повітря.

Запишімо формули для визначення відносної вологості повітря до випаровування води \((\mathbf{\varphi}_1)\) і після \((\mathbf{\varphi}_2):\)

де \(\mathbf{\rho}_\text{а}\) ‒ абсолютна вологість повітря, яка чисельно дорівнює масі \((m_1, m_2)\) водяної пари в певному об᾽ємі \(V\) повітря, \(\mathbf{\rho}_\text{НП}\) ‒ густина насиченої водяної пари, \(m\) ‒ маса води, яку випарували в кімнаті.

Із другої формули виразімо початкову відносну вологість повітря й обчислімо її, зваживши, що за умовою \(\mathbf{\varphi}_2=2\mathbf{\varphi}_1:\)

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.

Завдання скеровано на перевірку знання чинників, від яких залежить електроємність конденсатора, і вміння читати графіки.

Електроємність \(C\) плоского конденсатора з двох паралельних металевих пластин (обкладок), розділених шаром діелектрика, обчислюють за формулою $$ C=\frac{\mathbf{\varepsilon}\mathbf{\varepsilon}_0S}{d}, $$ де \(\mathbf{\varepsilon}_0\) ‒ електрична стала, \(\mathbf{\varepsilon}\) ‒ діелектрична проникність діелектрика, \(S\) ‒ площа пластини конденсатора, \(d\) ‒ відстань між пластинами.

З наведеної формули зрозуміло, що електроємність обернено пропорційна відстані між пластинами конденсатора: $$ C\sim \frac 1d. $$

Зі збільшенням відстані між пластинами електроємність конденсатора зменшуватиметься. Треба зауважити, що ця формула для визначення електроємності конденсатора справедлива лише за малих значень \(d.\)

Розгляньмо, як вплине діелектрик між пластинами конденсатора на його електроємність. Візьмемо до уваги, що в ізоляції конденсаторів використовують тонкі шари діелектрика.

Проаналізуймо зображені графіки. Якщо розглядати конденсатор без діелектрика, то його електроємність відмінна від нуля (як це зображено у варіанті відповіді Б) і має якесь початкове значення $$ C=\frac{\mathbf{\varepsilon}_0S}{d}. $$

Якщо ж заповнити простір між пластинами (обкладками) конденсатора діелектриком, то на електроємність конденсатора шар діелектрика впливає так: що більша його діелектрична проникність, то більшу електроємність має конденсатор порівняно з електроємністю такого самого конденсатора, діелектриком у якому є повітря.

Тому вміщення діелектрика між пластинами приведе до збільшення електроємності в \(\mathbf{\varepsilon}\) разів: $$ C=\mathbf{\varepsilon}\cdot \frac{\mathbf{\varepsilon}_0S}{d}. $$

Отже, варіанти відповіді В і Г не задовольняють умову завдання, оскільки зі збільшенням відстані між обкладками конденсатора для заповнення діелектриком електроємність за цими графіками зменшується.

Правильною відповіддю є варіант A (див. рисунок).

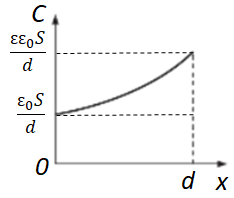
Відповідь: A.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з᾽єднання провідників.

Завдання скеровано на перевірку знання і розуміння особливостей з᾽єднання провідників і їхніх характеристик.

Під час послідовного з᾽єднання електричної лампи і резистора сила струму в них буде однаковою. Зваживши на характеристики лампи, обчислімо силу струму, який можна пропускати крізь неї: $$ P=UI, $$ де \(P\) ‒ потужність струму, \(U\) ‒ напруга, \(I\) ‒ сила струму; $$ I=\frac PU=\frac{75\ \text{Вт}}{36\ \text{В}}\approx 2\ \text{А}. $$

Щоб лампа працювала в нормальному режимі, треба крізь неї пропускати струм силою близько \(2\ \text{А}.\) Тоді із запропонованих резисторів підійде лише той, на якому є напис \(5\ \text{А},\ 50\ \text{Ом}.\) Інші резистори, про які йдеться в умові, можуть згоріти, тому що зазначена на них допустима сила струму менша за \(2\ \text{А}.\)

Відповідь: Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку знання особливостей електричного струму в різних середовищах.

Електричний струм у газах ‒ газовий розряд ‒ це напрямлений рух вільних електронів, позитивних і негативних йонів.

Електричний струм у розчинах і розплавах електролітів – це напрямлений рух вільних йонів.

Електричний струм у металах – напрямлений рух вільних електронів.

Провідність напівпровідників зумовлена рухом вільних і зв’язаних електронів (електронна і діркова провідності).

Отже, лише в розчині електроліту електричний струм відбувається без участі вільних електронів.

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.

Завдання скеровано на перевірку розуміння чинників, від яких залежить енергія магнітного поля.

Енергія магнітного поля \(W_\text{маг}\) провідника зі струмом дорівнює половині добутку індуктивності \(L\) провідника на квадрат сили струму \(I\) в провіднику: $$ W_\text{маг}=\frac{LI^2}{2}. $$

Енергія магнітного поля прямо пропорційна до квадрату сили струму: $$ W_\text{маг}\sim I^2. $$

Отже, якщо сила струму зросте втричі, то енергія магнітного поля збільшиться в \(9\) разів.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.

Завдання скеровано на перевірку розуміння, від яких чинників залежить період коливань нитяного маятника.

Період коливань \(T\) нитяного (математичного) маятника обчислюють за формулою $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) ‒ довжина маятника; \(g\) ‒ прискорення вільного падіння.

Згідно з формулою для визначення періоду, він не залежить від маси тягарця. Довжина нитки у формулі – під квадратним коренем, тож її треба збільшити в \(4\) рази, щоб період коливань маятника збільшився вдвічі.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння принципу роботи коливального контуру й особливостей перетворення енергії в ньому.

Під час розрядження конденсатора його заряд зменшуватиметься, а сила струму \(I\) в контурі ростиме. Відповідно енергія магнітного поля і модуль магнітної індукції поля котушки також збільшуватимуться: $$ W_\text{маг}=\frac{LI^2}{2}; $$ \(B\sim I\) (магнітна індукція прямо пропорційна до сили струму).

Енергію електричного поля \(W_\text{ел}\) зарядженого до напруги \(U\) конденсатора з електроємністю \(C\) і зарядом \(q,\) обчислюють за формулою $$ W_\text{ел}=\frac{qU}{2}, $$ тобто енергія електричного поля прямо пропорційна до заряду конденсатора \(W_\text{ел}\sim q,\) який під час розряджання зменшується. Унаслідок зменшення заряду зменшується енергія електричного поля конденсатора.

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Закони заломлення світла.

Завдання скеровано на перевірку знання, розуміння і застосування законів відбивання і заломлення світла.

Як зображено на рисунках А і Б, частина пучка зазнає дзеркального відбивання на верхній або нижній поверхні пластинки. У точках, де світло відбивається, уявно будуємо перпендикуляр до межі середовищ, і тоді за законами відбивання кут падіння дорівнює куту відбивання.

Також на рисунках Б і В заломлення показано правильно. Оскільки оптична густина скла більша за оптичну густину повітря, кут заломлення світла у склі має бути меншим від кута падіння світла з повітря.

На рисунку В на поверхнях плоскопаралельної пластинки світло двічі зазнає заломлення (після цього пучок поширюється в тому самому напрямку, але зміщується). Це правильно.

На рисунку Г не показано заломлення внаслідок перетинання світлом нижньої грані пластинки. Це неправильно.

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.

Завдання скеровано на перевірку знання і розуміння понять абсолютний і відносний показники заломлення світла.

Фізичну величину, яка характеризує оптичну густину середовища й показує, у скільки разів швидкість \(v\) поширення світла в середовищі менша, ніж у вакуумі, називають абсолютним показником \(n\) заломлення середовища: $$ n=\frac cv. $$

Звідси виразімо швидкість \(v\) поширення світла в середовищі: $$ v=\frac cn. $$

Також показник заломлення можна визначити як відношення синуса кута падіння до синуса кута заломлення: $$ n=\frac{\sin\ 45^\circ}{\sin\ 30^\circ}=\frac{\frac{\sqrt{2}}{2}}{\frac 12}=\frac{\sqrt{2}\cdot 2}{2\cdot 1}=\sqrt{2}. $$

Підставімо значення показника заломлення у формулу для швидкості: $$ v=\frac cn=\frac{c}{\sqrt{2}}. $$

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку знання постулатів теорії відносності Ейнштейна й розуміння відмінностей між класичною механікою і релятивістською.

Відповідно до другого постулату спеціальної теорії відносності швидкість поширення світла у вакуумі однакова в усіх інерціальних системах відліку. Це означає, що швидкість поширення світла у вакуумі інваріантна ‒ вона не залежить від швидкості руху джерела або приймача світла.

Час у класичній механіці І. Ньютона однаковий у будь-якій інерціальній системі відліку (СВ), тобто такі поняття, як зараз, раніше, пізніше, одночасно, не залежать від вибору СВ.

У релятивістській механіці час залежить від вибору СВ. Події, що відбулися в одній СВ одночасно, в іншій СВ можуть бути розділені часовим проміжком, тобто одночасність двох подій відносна.

Отже, згідно зі спеціальною теорією відносності в рухомій і нерухомій системах час плине по-різному, а швидкість світла у вакуумі однакова.

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Рівняння Ейнштейна для фотоефекту.

Завдання скеровано на перевірку розуміння явища фотоефекту.

Робота виходу \(A_\text{вих}\) ‒ це фізична величина, що характеризує метал і дорівнює енергії, яку треба передати електрону для того, щоб він зміг подолати сили, які утримують його на поверхні цього металу.

Рівняння Ейнштейна для зовнішнього фотоефекту: унаслідок поглинання фотона металом енергія фотона \((E_\text{ф}=hν)\) може бути повністю передана електрону й витрачена на здійснення роботи виходу \(A_\text{вих}\) та надання електрону кінетичної енергії \(E_{kmax}:\) \begin{gather*} E_\text{ф}=A_\text{вих}+E_{kmax},\\[7pt] hν=\frac{hc}{\mathbf{\lambda}_{max}}+E_{kmax}. \end{gather*}

Для кожної речовини існує максимальна довжина світлової хвилі \(\mathbf{\lambda}_{max}=\mathbf{\lambda}_{черв}\) (червона межа фотоефекту), за якої починається фотоефект.

Опромінення речовини світловими хвилями більшої довжини фотоефекту не викликає.

Максимальна довжина світлової хвилі (мінімальна частота) відповідає мінімальній енергії фотона: якщо \(hν\lt A_\text{вих},\) то електрони не вилітатимуть із речовини.

Умова $$ hν_{min}=\frac{hc}{\mathbf{\lambda}_{max}}=A_\text{вих} $$ визначає червону межу фотоефекту.

Обчислімо значення енергії, які відповідають тим довжинам хвиль, даним в умові:

Варіант відповіді Г неправильний, оскільки вже за довжини хвилі \(750\ \text{нм}\) не виникає струм у фотоелементі, а енергія \(1,5\cdot 10^{-19}\ \text{Дж}\) ще менша, ніж та, яку дає випромінювання з довжиною хвилі \(750\ \text{нм}.\)

За умовою випромінювання з довжиною хвилі \(600\ \text{нм}\) викликає фотострум, тобто енергії, яку дає це випромінювання, вистачає на роботу виходу і на кінетичну енергію, щоб утворювався фотострум.

Єдине менше значення енергії, ніж дає випромінювання з довжиною хвилі \(600\ \text{нм},\) це \(3\cdot 10^{-19}\ \text{Дж}\) ‒ варіант відповіді A ‒ це може бути робота виходу електронів з катода фотоелемента.

У варіантах відповіді Б і В значення енергії ще більші, отже, збільшується швидкість руху фотоелектронів.

Відповідь: A.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.

Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.

Запишімо реакцію розпаду ядра атома Урану: $$ \mathrm{^{238}_{\ \ 92}U\rightarrow\ ^{206}_{\ \ 82}Pb+}N_{\mathbf{\alpha}}\cdot\mathrm{^{4}_{2}He}+N_{\mathbf{\beta}}\cdot ^{\ \ \ 0}_{-1}e. $$

За нуклонним (масовим) числом визначімо кількість альфа-розпадів \(N_{\mathbf{\alpha}}:\) $$ N_{\mathbf{\alpha}}=\frac{238-206}{4}=8. $$

Перепишімо рівняння розпаду ядра атома Урану, зваживши на те, що альфа-розпадів було \(8:\) $$ \mathrm{^{238}_{\ \ 92}U\rightarrow\ ^{206}_{\ \ 82}Pb+8}\cdot\mathrm{^{4}_{2}He}+N_{\mathbf{\beta}}\cdot ^{\ \ \ 0}_{-1}e. $$

Тепер за протонним (зарядовим) числом визначімо, скільки було бета-розпадів. $$ N_{\mathbf{\beta}}=|92-82-8\cdot 2|=6. $$

Відповідь: Г.

ТЕМА: Механіка. Основи динаміки.

Завдання скеровано на перевірку розуміння різних динамічних процесів і вміння описати їх аналітично.

Ситуацію 1, коли відро з водою утримується за допомогою колодязного журавля (важеля), можна описати за допомогою правила моментів A: важіль перебуває в рівновазі, якщо сума моментів сил, які обертають важіль проти ходу годинникової стрілки, дорівнює сумі моментів сил, що обертають важіль за ходом годинникової стрілки.

Отже, умову рівноваги важеля під дією двох обертальних сил (сили тяжіння \(\overrightarrow{F}_1,\) що діє на відро з водою, і сили \(\overrightarrow{F}_2,\) прикладеної до іншого кінця колодязного журавля) можна записати як рівність моментів \(M_1\) і \(M_2\) відповідних сил: $$ M_1=M_2\ \text{або}\ F_1l_1=F_2l_2, $$ де \(l_1\) і \(l_2\) – плечі сил.

У разі деформації тіла, як то стискання пружини (2), із боку тіла починає діяти сила, яка прагне відновити той стан тіла, у якому воно перебувало до деформації. Цю силу називають силою пружності. У разі малих пружних деформацій розтягнення або стиснення сила пружності прямо пропорційна видовженню тіла (Б): $$ \overrightarrow{F}_\text{пружності}=-k\overrightarrow{x}. $$

Потужність, яку розвиває транспортний засіб, зручно визначати через силу тяги та швидкість руху. Формула справджується, і якщо в певний інтервал часу тіло рухається рівномірно, а напрямок сили тяги збігається з напрямком переміщення, і за нерівномірного руху: потужність \(P,\) яку розвиває двигун у певний момент часу, дорівнює добутку модуля сили тяги \(F\) двигуна на модуль його миттєвої швидкості \(v:\) $$ P=Fv. $$

Отже, ситуації 3 відповідає формула B.

Силу тертя ковзання можна зменшити, змастивши дотичні поверхні, як у ситуації 4, коли деталі механізмів змащують мастилом.

Рідке мастило віддаляє дотичні поверхні одну від одної − сухе тертя замінюється значно слабшим рідким тертям.

Сила тертя ковзання \(F_\text{тертя ковзання}\) не залежить від площі дотику тіл і прямо пропорційна до сили \(N\) нормальної реакції опори – формула Г: $$ F_\text{тертя ковзання}=\mathbf{\mu}N, $$ де \(\mathbf{\mu}\) – коефіцієнт тертя.

Відповідь: 1А, 2Б, 3В, 4Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Властивості газів, рідин і твердих тіл.

Завдання скеровано на знання і розуміння явищ молекулярної фізики і термодинаміки.

Молекули рідини безперервно рухаються (коливаються біля положень рівноваги, час від часу перестрибують із місця на місце), але сили притягання не дають їм розлетітися.

Проте в рідині завжди є молекули, кінетична енергія яких у кілька разів перевищує її середнє значення. Коли ці швидкі молекули опиняються на поверхні рідини, їхньої енергії вистачає для того, щоб, подолавши притягання сусідніх молекул, залишити рідину.

З погляду молекулярно-кінетичної теорії (МКТ) під час пароутворення з поверхні рідини вилітають найшвидші молекули. І саме пароутворення з поверхні рідини називають випаровуванням.

Отже, явищу 1 відповідає опис Д.

Середня кінетична енергія \(\overline{E}_k\) поступального руху молекул ідеального газу із середнім квадратом швидкості \(\overline{v^2}\) (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)) дорівнює: $$ \overline{E}_k=\frac{m_0\overline{v^2}}{2}. $$

Також середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32 kT, $$ де \(k\) ‒ стала Больцмана.

Отже, середня швидкість хаотичного руху молекул (середня квадратична швидкість руху молекул \(\overline{v}_\text{кв}=\sqrt{\overline{v^2}}\)) прямо пропорційна абсолютній температурі: $$ \overline{v}_\text{кв}\sim T. $$

Отже, під час охолодження (зниження температури) газу (2) середня швидкість хаотичного руху молекул також зменшується (Г).

Відповідно під час нагрівання (підвищення температури) газу (4) середня швидкість хаотичного руху молекул збільшуватиметься (А).

Плавлення ‒ це процес переходу речовини з твердого стану в рідкий.

Після досягнення температури плавлення тверде кристалічне тіло починає плавитися, а його температура не змінюється незважаючи на те, що нагрівник продовжує працювати й передавати тілу певну кількість теплоти. Уся енергія, що надходить від нагрівника, іде на руйнування кристалічної ґратки тіла. У цей інтервал часу внутрішня енергія твердого тіла продовжує збільшуватися. Отже, процесу 3 відповідає опис B.

Відповідь: 1Д, 2Г, 3В, 4А.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку знань про електричний струм у різних середовищах, а також розуміння і вміння застосовувати поняття, якими характеризують електричний струм у різних середовищах.

Електричний струм у газах ‒ газовий розряд ‒ це напрямлений рух вільних електронів, позитивних і негативних йонів.

Газовий розряд, який відбувається без дії зовнішнього йонізатора, називають самостійним газовим розрядом.

Розрізняють чотири види самостійних газових розрядів: іскровий, тліючий, дуговий, коронний.

Тліючий розряд виникає за невеликої напруги між електродами і низького тиску. Електрони розганяються до такої швидкості, що набувають енергії, достатньої для ударної йонізації. Тліючий розряд використовують у лампах денного світла (люмінесцентних трубках), кольорових газорозрядних трубках. Найважливіша галузь застосування ‒ квантові генератори світла (газові лазери).

Провідність напівпровідників зумовлена рухом вільних і зв’язаних електронів. Якщо до чистого напівпровідника додати невелику кількість певної домішки, то механізм його провідності зміниться. Оскільки за наявності домішок кількість носіїв струму збільшується (кожний атом домішки дає вільний електрон або дірку), провідність напівпровідників із домішками є набагато кращою, ніж провідність чистих напівпровідників.

Електричний струм у розчинах і розплавах електролітів – це напрямлений рух вільних йонів. Під час проходження електричного струму через електроліт відбувається перенесення хімічних складників електроліту. які виділяються на електродах ‒ осідають твердим шаром або виділяються в газуватому стані. Цей процес, пов’язаний з окисно-відновними реакціями на електродах, називають електролізом.

Електричний струм у металах – це напрямлений рух вільних електронів. З підвищенням температури питомий опір металу збільшується. Але в разі зниження температури майже до абсолютного нуля питомий опір деяких металів стрибком падає до нуля. Це явище називають надпровідністю. Наприклад, створення надпровідних ліній електропередачі дає змогу зекономити \(10–15\ \text{%}\) електроенергії. Водночас охолодження матеріалів до низьких температур досить затратне.

Діелектричною проникністю середовища називають фізичну величину, яка показує, у скільки разів напруженість електричного поля в речовині слабкіша від напруженості електричного поля у вакуумі.

Відповідь: 1В, 2А, 3Б, 4Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрації йонізувального випромінювання.

Завдання скеровано на перевірку знання і розуміння методів реєстрування йонізувального випромінювання.

Газорозрядний лічильник (лічильник Гейгера ‒ Мюллера) працює за таким принципом: робоче тіло ‒ газ ‒ розміщено в електричному полі з високою напругою; заряджена частинка, що пролітає крізь газ, йонізує його й у пристрої виникає газовий розряд: 1‒Д.

Камера Вільсона ‒ це трековий детектор. Камеру заповнено парою спирту або медичного ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують: 3‒Г.

Бульбашкова камера також є трековим детектором. Принцип її роботи подібний до камери Вільсона, а відмінність у тому, що робочим тілом у бульбашковій камері є перегріта рідина: йони, які виникають уздовж траєкторії руху частинки, стають центрами кипіння ‒ утворюється ланцюжок бульбашок: 2‒А.

Фотоемульсійний лічильник. Швидка заряджена частинка, рухаючись у шарі фотоемульсії, що містить кристали аргентум броміду \((\mathrm{AgBr}),\) на своєму шляху вириває електрони з деяких йонів Брому. Під час проявлення в змінених кристалах утворюються зерна срібла ‒ у шарі фотоемульсії проступають сліди (треки) первинної частинки й усіх заряджених частинок, що виникли внаслідок ядерних взаємодій. За товщиною і довжиною треків можна визначити заряди частинок та їхню енергію: 4‒В.

Відповідь: 1Д, 2А, 3Г, 4В.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу. Закон збереження енергії в механічних процесах.

Завдання скеровано на перевірку вміння застосовувати закони збереження імпульсу і енергії.

1. За умовою удар куль був непружний, центральний.

Якщо швидкості руху тіл до і після зіткнення (пружного чи непружного) напрямлені вздовж прямої, що проходить через центри мас цих тіл, таке зіткнення називають центральним.

Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію та нагрівання тіл), таке зіткнення називають непружним. Після такого удару тіла рухаються як єдине ціле.

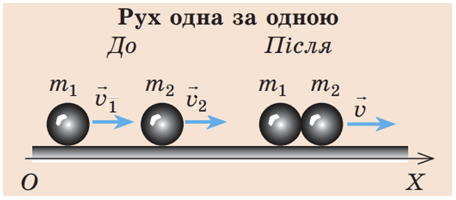
Опишімо рух куль до і після удару за допомогою закону збереження імпульсу у векторному вигляді та в проєкціях на вісь \(OX:\) \begin{gather*} m_1\overrightarrow{v}_1+m_2\overrightarrow{v}_2=(m_1+m_2)\overrightarrow{v},\\[7pt] m_1v_1+m_2v_2=(m_1+m_2)v, \end{gather*} де \(m_1\) ‒ маса більшої кулі, що рухалася з більшою швидкістю \(\overrightarrow{v}_1,\ m_2\) ‒ маса меншої кулі, що рухалася з меншою швидкістю \(\overrightarrow{v}_2,\ \overrightarrow{v}\) – швидкість руху куль після удару.

Обчислімо швидкість руху куль після удару:

Відповідь: 4.

2. Запишімо закон збереження енергії: \begin{gather*} \frac{m_1v^2_1}{2}+\frac{m_1v^2_2}{2}=\frac{(m_1+m_2)v^2}{2}+Q, \end{gather*} де \(Q\) ‒ утрачена кінетична енергія після удару куль.

Обчислімо її:

Відповідь: 0,6.

Відповідь: 1. 4. 2. 0,6.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і вміння будувати зображення в тонкій лінзі і плоскому дзеркалі.

Побудуймо хід променів відповідно до умови завдання: після проходження крізь лінзу (один промінь паралельно головній оптичній осі і далі уявно через фокус лінзи, а другий промінь ‒ через оптичний центр лінзи не заломлюючись) промені за законами відбивання відбиваються від плоского дзеркала під тими самими кутами, що й упали на дзеркало, і знову проходять крізь лінзу (див. рисунок).

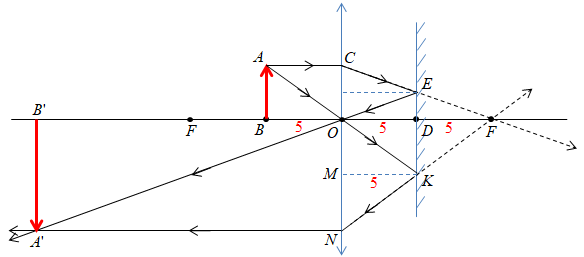
1. Розгляньмо прямокутні \(\Delta COF\) і \(\Delta EDF:\) вони подібні за гострим кутом, отже, \(\frac{OF}{OD}=\frac{10}{5}=2,\) відповідно \(\frac{CO}{ED}=2,\) звідки \(ED=\frac 12 CO,\) і відповідно \(ED=\frac 12 AB,\) тобто дорівнюватиме половині висоти \(AB\) предмета.

Розгляньмо прямокутні \(\Delta ABO\) і \(\Delta OMK:\) вони рівні за катетом і прилеглим гострим кутом. Також \(\Delta OMK = \Delta NMK\) (за побудовою):

\(A'B'ON\) ‒ прямокутник (за побудовою), \(ON = A'B'.\)

Розгляньмо прямокутні \(\Delta CDO\) і \(\Delta A'B'O:\) вони подібні за гострим кутом, отже, $$ \frac{ED}{A'B'}=\frac{OD}{B'O}=\frac 14. $$

Отже, $$ B'O=OD\cdot 4=20\ \text{см}, $$ де \(B'O\) ‒ відстань від лінзи до зображення \(A'B'\) предмета \(AB.\)

Відповідь: 20.

2. Як уже було доведено в пункті 1, $$ AB=\frac 12 ON,\ \text{а}\ ON=A'B', $$ отже, $$ AB=\frac 12 A'B'. $$ А це означає, що така система дає збільшення у \(2\) рази.

Відповідь: 2.

Відповідь: 1. 20. 2. 2.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння характеру руху тіл.

Позначимо сталу – модуль швидкості руху потягу – \(v.\) Тоді відстань \(s_\text{п},\) яку пройшов потяг за час \(t\) від моменту відчеплення до моменту зупинки вагона, можна визначити за формулою для обчислення відстані під час прямолінійного рівномірного руху: $$ s_\text{п}=v\cdot t. $$

Час руху потяга на цьому відрізку шляху такий самий, як і час руху відчепленого останнього вагона до зупинки. Вагон рівномірно сповільнюватиметься. Його початковою швидкістю \(v_0\) буде швидкість руху потягу \(v,\) а кінцева швидкість \(v_\text{к}\) дорівнюватиме нулю.

Отже, $$ s_\text{в}=\frac{v_0+v_\text{к}}{2}\cdot t=\frac v2\cdot t, $$ де \(s_\text{в}\) ‒ відстань, яку пройшов вагон до зупинки.

Виразімо із цієї формули час руху вагона \(t\) і підставімо цей вираз у формулу для відстані, яку пройшов потяг:

Відповідь: 400.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку розуміння переходу кількості теплоти під час теплових процесів.

Запишімо рівняння теплового балансу для процесу, описаного в умові завдання: $$ Q_1=Q_2+Q_3, $$ де \(Q_1\) ‒ це кількість теплоти, що віддасть вода льоду, \(Q_2\) ‒ кількість теплоти, необхідна, щоб нагріти лід від температури \(‒10\ ^\circ \mathrm{C}\) до температури плавлення \(0 ^\circ \mathrm{C},\) \(Q_3\) ‒ кількість теплоти, потрібна для плавлення льоду.

Під час плавлення температура льоду не змінюватиметься, оскільки вся кількість теплоти піде на руйнування кристалічних ґраток льоду і перехід його з твердого стану в рідкий.

Отже, кінцевою температурою води, яку доливатимемо в посудину, і води, яку отримаємо після плавлення (танення) льоду, буде температура \(0 ^\circ \mathrm{C}.\) \begin{gather*} Q_1=c_\text{в}m_\text{в}(t_\text{в}-0), \end{gather*} де \(c_\text{в}\) ‒ питома теплоємність води, \(m_\text{в}\) ‒ шукана маса води, \(t_\text{в}\) ‒ початкова температура води; $$ Q_2=c_\text{л}m_\text{л}(0-t_\text{л}), $$ де \(c_\text{л}\) ‒ питома теплоємність льоду, \(m_\text{л}\) ‒ маса льоду, \(t_\text{л}\) ‒ початкова температура льоду; $$ Q_3=\mathbf{\lambda}m_\text{л}, $$ де \(\mathbf{\lambda}\) ‒ питома теплоємність плавлення льоду.

Підставімо всі вирази для кількості теплоти в рівняння теплового балансу й визначімо необхідну масу води: \begin{gather*} c_\text{в}m_\text{в}(t_\text{в}-0)=c_\text{л}m_\text{л}(0-t_\text{л})+\mathbf{\lambda}m_\text{л},\\[6pt] m_\text{в}=\frac{m_\text{л}(c_\text{л}(0-t_\text{л})+\mathbf{\lambda})}{c_\text{в}(t_\text{в}-0)}. \end{gather*}

Зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: $$ \Delta T=\Delta t, $$ де \(T\) ‒ абсолютна температура за шкалою Кельвіна, тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: $$ 1\ ^\circ \mathrm{C}=1\ \text{K}. $$

Відповідно

Відповідь: 8,5.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.

Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати різними способами коефіцієнт корисної дії та фізичні величини, які на нього впливають.

Коефіцієнт корисної дії (ККД) \(\mathbf{\eta}\) ‒ фізична величина, якою характеризують економічність теплового двигуна. Він дорівнює відношенню корисної роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \mathbf{\eta}=\frac AQ. $$

Корисна робота двигуна полягає в подоланні сили опору руху візка \(F:\) $$ A=F\cdot s=F\cdot vt, $$ де \(s\) ‒ шлях, який долає візок, за час \(t,\ v\) ‒ швидкість руху візка.

Також коефіцієнт корисної дії такого двигуна можна визначити за формулою $$ \mathbf{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівника; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняймо ці два вирази для обчислення коефіцієнта корисної дії: \begin{gather*} \frac AQ=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}},\\[6pt] \frac{F\cdot vt}{Q}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}. \end{gather*}

Виразімо звідси модуль швидкості руху візка й обчислімо його:

Відповідь: 2.

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку розуміння, що є корисною, а що – повною кількістю теплоти під час роботи електронагрівача.

Запишімо формулу для визначення коефіцієнта корисної дії \(\mathbf{\eta}\) нагрівача електрочайника: \begin{gather*} \mathbf{\eta}=\frac{Q_\text{к}}{Q_\text{п}}\cdot 100\ \text{%}, \end{gather*} де \(Q_\text{к}\) ‒ корисна кількість теплоти, яка потрібна, щоб довести воду за температури \(34\ ^\circ \text{C}\) до кипіння \((100\ ^\circ \text{C}),\) \(Q_\text{п}\) ‒ повна кількість теплоти, що може виділитися під час проходження електричного струму через нагрівач електрочайника.

У формулі $$ Q_\text{к}=cm(t_\text{к}-t_\text{в})=c\mathbf{\rho}V(t_\text{к}-t_\text{в}) $$ \(c\) ‒ питома теплоємність, \(m\) ‒ маса, \(t_\text{к}\) ‒ температура кипіння, \(t_\text{в}\) ‒ температура, \(\mathbf{\rho}\) ‒ густина, \(V\) ‒ об᾽єм води.

Повну кількість теплоти можна визначити за законом Джоуля ‒ Ленца:

Або ж за формулою для визначення роботи \(A\) електричного струму: \begin{gather*} Q_\text{п}=A=UI\mathbf{\tau} \end{gather*} де \(U\) ‒ напруга в мережі, \(I\) ‒ сила струму, \(\mathbf{\tau}\) ‒ час, протягом якого нагрівали воду.

Підставмо вирази для корисної і повної кількості теплоти у формулу для коефіцієнта корисної дії і визначимо силу струму:

Відповідь: 6,25.

ТЕМА: Електродинаміка. Основи електростатики. Потенціал, різниця потенціалів.

Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки в електричному полі.

Силові лінії поля напрямлені завжди в бік зменшення потенціалу, а порошинка рухається в напрямку, протилежному до напрямку силових ліній електричного поля, отже, потенціал \(\mathbf{\varphi}_2\) точки, у якій порошинка зупиниться, буде більший за потенціал \(\mathbf{\varphi}_1\) точки, з якої вона вилітає:

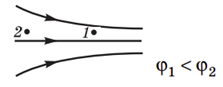
Скористаймося законом збереження енергії порошинки в електричному полі: $$ q\mathbf{\varphi}_1+\frac{mv^2_1}{2}=q\mathbf{\varphi}_2+\frac{mv^2_2}{2}, $$ де вирази \(q\mathbf{\varphi}_1\) і \(q\mathbf{\varphi}_2\) ‒ це потенціальні енергії порошинки в точках поля з певним потенціалом, а вирази \(\frac{mv^2_1}{2}\) і \(\frac{mv^2_2}{2}\) ‒ це кінетичні енергії порошинки в цих точках.

Візьмемо до уваги, що $$ v_2=0, $$ бо за умовою порошинка має зупинитися, а заряд порошинки позитивний.

Відповідно

Відповідь: 200.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на перевірку застосування закону Ома для повного кола.

Запишімо закон Ома для повного кола для обох ситуацій: \begin{gather*} I_1=\frac{\mathbf{\varepsilon}}{R_1+r},\\[6pt] I_2=\frac{\mathbf{\varepsilon}}{R_2+r}, \end{gather*} де \(I_1\) ‒ сила струму, коли підключили зовнішній опір \(R_1,\)
\(I_2\) ‒ сила струму, коли підключили зовнішній опір \(R_2,\)
\(\mathbf{\varepsilon}\) ‒ електрорушійна сила джерела струму,
\(r\) ‒ внутрішній опір джерела струму.

Електрорушійна сила і внутрішній опір джерела струму є його сталими характеристиками, який би зовнішній опір не підключали. Тому виразімо електрорушійну силу з обох формул і прирівняємо ці вирази: \begin{gather*} \mathbf{\varepsilon}=I_1R_1+I_1r=U_1+\frac{U_1}{R_1}\cdot r,\\[6pt] \mathbf{\varepsilon}=I_2R_2+I_2r=U_2+\frac{U_2}{R_2}\cdot r,\\[6pt] U_1+\frac{U_1}{R_1}\cdot r=U_2+\frac{U_2}{R_2}\cdot r. \end{gather*}

Виведімо формулу для обчислення внутрішнього опору джерела струму:

Відповідь: 4.

ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.

Завдання скеровано на перевірку знання принципу дії дифракційної ґратки й розуміння формули, що описує її.

Запишімо формулу дифракційної ґратки: $$ d\cdot \sin\mathbf{\varphi}=k\mathbf{\lambda}, $$ де \(d\) ‒ період або стала ґратки ‒ загальна ширина непрозорої і прозорої ділянок, кут \(\mathbf{\varphi}\) ‒ шуканий кут, під яким спостерігають дифракційний максимум другого порядку, \(k\) ‒ ціле число, відповідає максимуму певного порядку (тут \(k=2\)), \(\mathbf{\lambda}\) ‒ довжина світлової хвилі.

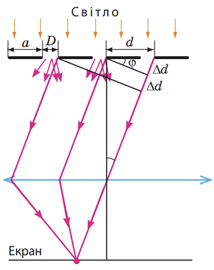
Обчислімо спочатку синус кута \(\mathbf{\varphi}\), а потім градусну міру кута: \begin{gather*} $1\mathbf{\varphi}=\frac{k\mathbf{\lambda}}{2},\\[6pt] $1\mathbf{\varphi}=\frac{2\cdot 500\cdot 10^{-9}\ \text{м}}{2\cdot 10^{-6}\ \text{м}}=0,5,\\[6pt] \mathbf{\varphi}=30^\circ. \end{gather*}

Відповідь: 30.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Поділ ядер Урану.

Завдання скеровано на перевірку розуміння поділу ядер урану.

Спочатку обчислімо кількість \(N\) ядер Урану, які мають розпастися з вивільненням енергії \(96\ \text{МДж}.\) Розділимо цю загальну енергію на енергію поділу одного ядра:

Кількість структурних частинок речовини можна визначити, знаючи \(m\) ‒ масу речовини, \(M\) ‒ молярну масу речовини, \(N_\mathrm{A}\) ‒ сталу Авогадро: $$ N=\frac mM\cdot N_\mathrm{A}. $$

Звідси виразімо масу ядер Урану й обчислімо її:

Відповідь: 1,175.