ЗНО онлайн 2016 року з фізики – основна сесія

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на перевірку вміння застосовувати другий закон Ньютона.

Другий закон Ньютона: прискорення \(\overrightarrow{a},\) якого набуває тіло внаслідок дії сили \(\overrightarrow{F},\) прямо пропорційне цій силі та обернено пропорційне масі \(m\) тіла: $$ \overrightarrow{a}=\frac{\overrightarrow{F}}{m}. $$

Виразімо з формули шукану величину масу й запишімо її у проєкціях на горизонтальну вісь \(Ox,\) уздовж якої рухається тіло: $$ m=\frac Fa. $$

Визначмо прискорення як відношення зміни швидкості руху тіла до інтервалу часу, за який ця зміна відбулася (теж у проєкціях на вісь \(Ox\)): $$ a=\frac{v-v_0}{t}, $$ де \(v_0\) ‒ початкова швидкість руху тіла в момент початку відліку часу, \(v\) ‒ швидкість руху тіла через деякий інтервал часу \(t.\)

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу рівномірного й рівноприскореного рухів.

Завдання скеровано на перевірку вміння читати графіки й описувати їх кінематичними рівняннями.

Оскільки графіками залежності координати \(x\) від часу \(t\) є ділянки прямих, то за характером руху та за формою траєкторії це рівномірний прямолінійний рух. Для рівномірного прямолінійного руху рівняння координати таке: $$ x=x_0+v_\mathrm{x}t, $$ де \(x_0\) ‒ початкова координата, \(v_\mathrm{x}\) ‒ проєкція швидкості на горизонтальну вісь, уздовж якої рухається тіло.

Розгляньмо кожен момент часу, коли змінюються графіки.

Запишімо рівняння координати для ділянок від \(0\) до \(1,5\ \text{с}\) кожного графіка, скорочено позначивши дані щодо кольору графіків: чорний ‒ «ч» і сірий ‒ «с» відповідно:

Отже, у момент часу \(1\) с швидкості руху тіл різні.

Розгляньмо ділянки від \(1,5\) до \(2,5\ \text{с}\) обох графіків і запишімо рівняння координати для цих ділянок:

Отже, у момент часу \(2\ \text{с}\) швидкості руху обох тіл однакові \(v_{2\text{ч}}=v_{2\text{с}}.\) Знак «мінус» указує на те, що тіла рухались у напрямку, протилежному до напрямку вибраної горизонтальної осі.

Розгляньмо ділянки від \(2,5\ \text{с}\) обох графіків і запишімо рівняння координати для цих ділянок:

Отже, у моменти часу \(3\ \text{с}\) і \(4\ \text{с}\) швидкості руху тіл різні.

Можна, не обчислюючи значення швидкості для кожного моменту часу, визначити, які ділянки графіків відповідатимуть однаковим швидкостям.

Рівняння координати \(x=x_0+v_\mathrm{x}t\) відповідає лінійній математичній функції \(y=b+kx\) (рис. 1). Коефіцієнт \(k\) називають кутовим коефіцієнтом цієї функції.

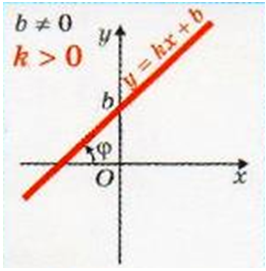
Рис. 1. Графік лінійної функції, яка зростає

Від коефіцієнта \(k\) залежить кут, який побудована пряма утворює з додатним напрямком осі \(Ox.\) На рисунку 2 показано паралельні прямі з однаковим кутовим коефіцієнтом \(k.\)

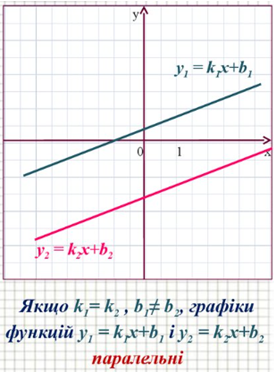
Рис. 2. Прямі з однаковим кутовим коефіцієнтом \(k\)

Отже, використавши геометричний зміст графіків, наведених в умові, можна без обчислень дійти висновку, що швидкості руху будуть однакові, якщо ділянки графіків нахилені під однаковим кутом до осі \(Ox,\) тобто паралельні між собою. Це відповідає моменту часу \(2\ \text{с}.\)

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на перевірку розуміння графіків функціональної залежності фізичних величин, що ними описано прямолінійний рівноприскорений рух.

Кінетична енергія \(E_\text{к}\) ‒ це фізична величина, яка є характеристикою механічного стану рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху: $$ E_\text{к}=\frac{mv^2}{2}. $$

Отже, кінетична енергія пропорційна квадрату швидкості \(E_\text{к}\sim v^2.\) Рух тіла, кинутого вертикально вгору, є рівноприскореним, тому швидкість руху визначмо за відповідним кінематичним рівнянням (у проєкціях на вертикальну, напрямлену вгору вісь \(Oy\)): $$ v=v_0->. $$

З рівняння випливає, що швидкість руху тіла прямо пропорційна часу: $$ v\sim t, $$ відповідно квадрат швидкості пропорційний квадрату часу: $$ v^2\sim t^2. $$

Тож і кінетична енергія пропорційна квадрату часу: $$ E_\text{к}\sim t^2. $$

Графіком залежності кінетичної енергії від часу (квадратичної функції) є парабола. З огляду на це варіанти відповіді А і Г неправильні.

Оскільки тіло піднімається, то кінетична енергія зменшуватиметься, тіло сповільнюватиметься, а потенціальна енергія зростатиме. Такому рухові відповідатиме парабола, вітки якої напрямлені вгору: із плином часу кінетична енергія зменшуватиметься до нуля у максимальній точці підняття, а коли тіло почне падати, кінетична енергія почне зростати до початкового значення, оскільки за умовою опором повітря нехтуємо, утрат механічної енергії немає.

Відповідь: Б.

ТЕМА: Механіка. Елементи механіки рідин та газів. Тиск. Закон Паскаля для рідин та газів.

Завдання скеровано на перевірку розуміння принципу роботи гідравлічного преса.

Гідравлічний прес ‒ це найпростіша гідравлічна машина, яку використовують для створення великих сил тиску (див. рисунок).

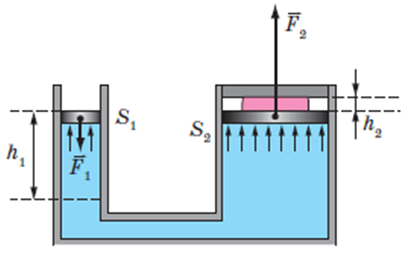
Якщо до поршня меншого циліндра прикласти силу \(\overrightarrow{F}_1,\) то ця сила чинитиме на поверхню рідини певний додатковий тиск \(p:\) $$ p=\frac{F_1}{S_1}, $$ де \(S_1\) ‒ площа меншого поршня.

За законом Паскаля цей тиск передаватиметься в усі точки рідини, якою заповнені сполучені циліндри. Тож рідина почне тиснути з певною силою \(\overrightarrow{F}_2\) на поршень більшого циліндра: $$ F_2=p\cdot S_2, $$ де \(S_2\) ‒ площа більшого поршня; \(p\) ‒ додатковий тиск.

Отже, сила, що діє з боку рідини на великий поршень, більша від сили, що діє на малий поршень, у стільки разів, у скільки разів площа великого поршня більша за площу малого: $$ \frac{F_2}{F_1}=\frac{S_2}{S_1}, $$ де \(\frac{F_2}{F_1}\) ‒ це виграш у силі.

Використанням гідравлічного преса забезпечено виграш у силі й, водночас, програш у відстані та, відповідно, швидкості. Час опускання меншого поршня такий самий, як і час піднімання більшого поршня. А відстань \(h_1,\) яку проходить менший поршень, більша за відстань \(h_2,\) яку долає більший поршень (див. рисунок). Тоді менший поршень мусить рухатися з більшою швидкістю \(v_1,\) щоб за той самий час подолати більшу відстань:

Відповідь: Г.

ТЕМА: Молекулярна фізика та термодинаміка. Основи молекулярно-кінетичної теорії.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=\mathrm{const}, $$ із якого випливає, що абсолютна температура \(T\) прямо пропорційна добутку тиску \(p\) й об’єму \(V.\)

Розгляньмо кожен зі станів 1‒4 ідеального газу. Одну клітинку вважатимемо одиничним відрізком для обох величин: \begin{gather*} \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf1\\[7pt] T_1\sim 5p\cdot 1V\sim 5pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf2\\[7pt] T_2\sim 4p\cdot 2V\sim 8pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf3\\[7pt] T_3\sim 3p\cdot 3V\sim 9pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf4\\[7pt] T_4\sim 1p\cdot 6V\sim 6pV. \end{gather*}

Отже, найменшим є числовий коефіцієнт у стані \(1,\) температура газу буде найменшою у стані \(1.\)

Відповідь: A.

ТЕМА: Молекулярна фізика та термодинаміка. Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл.

Завдання скеровано на перевірку розуміння процесів переходу речовини з твердого в рідкий стан.

Кристалічні речовини починають плавитися після досягнення ними певної (власної для кожної речовини) температури. Для цього речовину треба нагрівати, що відображено на ділянці графіка 1‒2: із часом температура підвищується.

Під час плавлення температура речовини не змінюється. Уся енергія (кількість теплоти), що надходить до речовини, витрачається на руйнування кристалічної ґратки. Цьому етапу процесу відповідає ділянка графіка 2‒3, де температура залишається сталою.

Отже, точка 2 відповідає початку плавлення речовини.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів.

Кількість теплоти \(Q,\) передана системі, забезпечує зміну внутрішньої енергії системи \(\Delta U\) та виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Під час ізохорного нагрівання об’єм газу не змінюється \(\Delta V=0,\) газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=\Delta U. $$

В ізохорному процесі вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу. Тож внутрішня енергія газу збільшилася на \(12\ \text{кДж.}\)

Під час ізотермічного розширення температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=A. $$

В ізотермічному процесі вся передана газу кількість теплоти витрачається на виконання механічної роботи. Тому внутрішня енергія не змінилася на цьому етапі перетворень із газом.

Отже, за результатами двох процесів, що відбулися з газом, його внутрішня енергія змінилася лише на \(12\ \text{кДж.}\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Принцип дії теплових двигунів. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.

Завдання скеровано на перевірку вміння розв’язувати задачі щодо принципу роботи і коефіцієнта корисної дії теплового двигуна.

Принцип роботи теплових двигунів такий: робоче тіло, одержуючи певну кількість теплоти \(Q_1\) від нагрівача, виконує механічну роботу \(A\) і передає деяку кількість теплоти \(Q_2\) холодильнику.

З одного боку, коефіцієнт корисної дії \(\mathbf{\eta}\) двигуна дорівнює відношенню роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q_1,\) одержуваної від нагрівача: $$ \mathbf{\eta}=\frac{A}{Q_1}. $$

З іншого боку, коефіцієнт корисної дії \(\mathbf{\eta}\) ідеальної теплової машини дорівнює: $$ \mathbf{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівача; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняємо праві частини обох формул: $$ \frac{A}{Q_1}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ звідки $$ Q_1=\frac{A\cdot T_\text{Н}}{T_\text{Н}-T_\text{Х}}. $$

Перед тим, як обчислити шукану кількість теплоти, визначмо температуру в кельвінах (K):

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.

Завдання скеровано на перевірку знання і розуміння принципу суперпозиції електричних полів.

Модуль напруженості \(\overrightarrow{E}\) електричного поля, створеного точковим зарядом \(Q\) на відстані \(r\) від цього заряду, обчислюють за формулою $$ E=k\frac{|Q|}{r^2}, $$ де \(k\) ‒ коефіцієнт пропорційності.

Оскільки за умовою є два електричні заряди, то діятиме принцип суперпозиції (накладання) електричних полів: напруженість електричного поля системи зарядів у даній точці простору дорівнює векторній сумі напруженостей полів, які створюються цими зарядами в точці (див. рисунок).

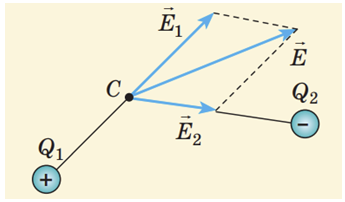
Розглянувши на рисунку в умові завдання взаємне розташування кульок і точок і взявши до уваги, що в кульок \(A\) і \(B\) однакові електричні заряди, можна дійти висновку, що напруженість буде мінімальною, а саме дорівнюватиме нулю в точці \(2.\) Кульки \(A\) і \(B\) по різні боки від точки \(2\) й на однакових відстанях від неї. Отже, вектори напруженості будуть напрямлені протилежно один до одного і в сумі дадуть нуль, оскільки за модулем напруженості (див. формулу вище) однакові.

В усіх інших ситуаціях вектор суми напруженостей відмінний від нуля, тож правильною відповіддю є точка симетрії – точка \(2.\)

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище електромагнітної індукції.

Завдання скеровано на перевірку розуміння виникнення індукційного струму.

Розглянутий у завданні дослід є одним із сучасних варіантів дослідів Майкла Фарадея, завдяки яким він дійшов висновку: у замкненому провідному контурі (котушці) виникає електричний струм, якщо кількість ліній магнітної індукції, що пронизують поверхню, обмежену контуром, змінюється. Це явище було названо електромагнітною індукцією, а електричний струм, який під час цього виникає, ‒ індукційним (наведеним) струмом.

У цьому досліді, як зображено на схематичному рисунку, ліву котушку через вимикач приєднано до джерела струму, а праву котушку замкнено на гальванометр. Якщо розмикати чи замикати коло лівої котушки, то в правій котушці виникне індукційний струм.

Кількість ліній магнітної індукції, що пронизують певну поверхню, характеризують фізичною величиною – потоком магнітної індукції або магнітним потоком. Магнітний потік максимальний, якщо поверхня, яку пронизують лінії магнітної індукції, перпендикулярна до цих ліній.

Лінії магнітної індукції магнітного поля найщільніше розташовані біля полюсів котушки і проходять перпендикулярно до площини перерізу котушки (див. рисунок). Тобто найбільша кількість ліній магнітної індукції пройде крізь котушку з гальванометром, коли осі котушок збігатимуться, як це зображено на рисунку у варіанті відповіді Г.

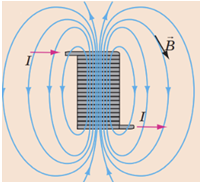
Відповідь: Г.

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку вміння обчислювати потужність струму за послідовного з’єднання провідників.

Визначмо спочатку загальну потужність \(P_1\) струму в однакових резисторах опором \(R=10\ \text{Ом}\) кожен. Оскільки за умовою напруга \(U\) на полюсах батареї незмінна, то для визначення потужності \(P_1\) скористаємося такою формулою $$ P_1=\frac{U^2}{R_\text{заг1}}=\frac{U^2}{3R}=\frac{U^2}{30\ \text{Ом}}, $$ де \(R_\text{заг1}\) ‒ загальний опір ділянки електричного кола з трьох послідовно з’єднаних резисторів у першому випадку.

Якщо ж замінити один резистор опором \(R=10\ \text{Ом}\) на резистор опором \(r=4\ \text{Ом},\) то загальну потужність \(P_2\) струму в другому випадку визначатимемо за формулою $$ P_2=\frac{U^2}{R_\text{заг2}}=\frac{U^2}{2R+r}=\frac{U^2}{24\ \text{Ом}}. $$

Для визначення загального опору ділянки кола за послідовного з’єднання провідників (резисторів) їхні опори додають.

Обчислімо, у скільки разів змінилася потужність струму в резисторах: $$ \frac{P_2}{P_1}=\frac{U^2\cdot 30\ \text{Ом}}{24\ \text{Ом}\cdot U^2}=\frac{30}{24}=1,25\ \text{раза}. $$

Отже, потужність струму \(P_2\) збільшилася в \(1,25\) раза.

Відповідь: A.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Закони електролізу.

Завдання скеровано на перевірку знання і застосування першого закону Фарадея для електролізу.

За першим законом Фарадея для електролізу маса речовини, яка виділяється на електроді під час електролізу, прямо пропорційна силі струму \(I\) та часу \(t\) його проходження через електроліт: $$ m=kIt,\ \text{або}\ m=kq, $$ де \(q\) ‒ заряд, що пройшов через електроліт; \(k\) ‒ коефіцієнт пропорційності, який називають електрохімічним еквівалентом.

Візьмемо до уваги: $$ kq=kIt\Rightarrow q=It\Rightarrow I=\frac qt. $$

Формулою \(I=\frac qt\) математично описано фізичний зміст сили струму як величини, якою характеризують електричний струм.

Обчислімо силу струму: $$ I=\frac{60\ \text{Кл}}{60\ \text{с}}=1\ \text{А}. $$

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.

Завдання скеровано на перевірку вміння застосовувати формулу для періоду нитяного маятника.

Період коливань \(T\) нитяного (математичного) маятника обчислюють за формулою $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) ‒ довжина маятника; \(g\) ‒ прискорення вільного падіння.

Запишімо формули періоду коливань для першого і другого маятників:

Виразімо довжини маятників через кількість клітинок, позначивши буквою \(l\) довжину сторони однієї клітинки:

Поділімо ліві і праві частини формул для періодів обох маятників й обчислімо значення періоду коливань маятника \(2:\)

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає плоске дзеркало.

Завдання скеровано на перевірку розуміння побудови зображень у плоскому дзеркалі.

Загальні характеристики зображень у плоских дзеркалах

1. Плоске дзеркало дає уявне зображення предмета: частина відбитих від дзеркала променів потрапляє до вашого ока і вам здається, що відбиті за законом відбивання промені виходять із точки \(S_1,\) хоча насправді джерела світла в точці \(S_1\) немає. У ній перетинаються уявні продовження відбитих променів ‒ \(AA_1,\) \(BB_1,\) \(CC_1.\) Точку \(S_1\) називають уявним зображенням точки \(S\) (див. рисунок).

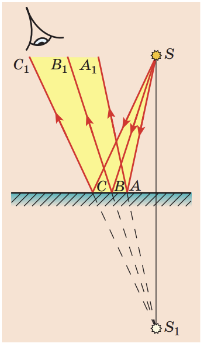
2. Зображення предмета в плоскому дзеркалі та власне предмет є симетричними відносно поверхні дзеркала:
1) зображення предмета дорівнює за розміром самому предмету;
2) зображення предмета розташоване на тій самій відстані від поверхні дзеркала, що й предмет;
3) відрізок, який сполучає точку на предметі з відповідною їй точкою на зображенні, є перпендикулярним до поверхні дзеркала.

Тому зображенням точки \(A\) в плоскому дзеркалі є точка \(\boldsymbol 3\) ‒ відрізок, який з’єднує точку \(A\) і точку \(\boldsymbol 3\) перпендикулярний до площини дзеркала, і точка \(A\) і точка \(\boldsymbol 3\) лежать на однаковій відстані від дзеркала по різні його боки. Точка \(\boldsymbol 1\) не може бути зображенням, тому що лежить з того ж боку дзеркала, що й точка \(A,\) тож це дійсне зображення. Точки \(\boldsymbol 2\) й \(\boldsymbol 4\) є уявними, але відрізки, що сполучають точку \(A\) з точками \(\boldsymbol 2\) й \(\boldsymbol 4,\) не є перпендикулярними до площини дзеркала й розташовані не на тій самій відстані від нього, що й точка \(A.\)

Відповідь: B.

ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Електромагнітні хвилі та швидкість поширення їх.

Завдання скеровано на перевірку розуміння поширення електромагнітної хвилі через її характеристики.

Електромагнітну хвилю як процес поширення електромагнітного поля насамперед характеризують векторами напруженості \(\overrightarrow{E}\) і магнітної індукції \(\overrightarrow{B}.\) Будь-яка хвиля періодична і в часі, і в просторі, тому зазначені величини періодично змінюються і з часом, і зі зміною відстані від джерела хвилі. За теорією Максвелла вектори \(\overrightarrow{E}\) і \(\overrightarrow{B}\) одночасно сягають максимального значення й одночасно перетворюються на нуль, під час цього вони перпендикулярні як один до одного, так і до напрямку поширення хвилі (див. рисунок). Отже, електромагнітна хвиля ‒ це поперечна хвиля:

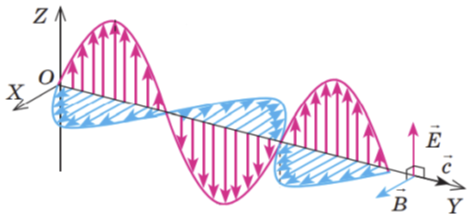
Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку розуміння перетворень у коливальному контурі під час вільних електромагнітних коливань.

За час одного коливання (період) у коливальному контурі конденсатор перезаряджається двічі. Протягом першої чверті періоду заряд на обкладках конденсатора зменшується до нуля \((q=0).\)

Після проходження котушки заряджені частинки продовжують рух у тому самому напрямку, а конденсатор перезаряджається ‒ заряд на його обкладках змінюється на протилежний. Отже, протягом другої чверті періоду конденсатор повністю заряджається \((q=q_{max}).\)

Наступну (третю) чверть періоду конденсатор знову розряджатиметься, однак уже в зворотному напрямку. Коли мине три чверті періоду, конденсатор повністю розрядиться, заряд дорівнюватиме нулю \((q=0).\)

За останню чверть періоду конденсатор зарядиться до максимального значення \((q=q_{max})\) з тими ж знаками електричного заряду на його обкладках, які були на початок коливання.

Отже, тієї миті, коли від початку коливання минуло три чверті періоду коливання, заряд на пластинах конденсатора дорівнюватиме нулю \((q=0).\)

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку розуміння законів релятивістської механіки.

Відповідно до другого постулату спеціальної теорії відносності (СТВ) швидкість поширення світла у вакуумі є незмінною і не залежить від швидкості руху джерела або приймача світла. Це означає, що класичний закон додавання швидкостей у релятивістській механіці застосовувати не можна. У СТВ застосовують релятивістський закон додавання швидкостей. Запишімо цей закон для ситуації, описаній в умові завдання: $$ v_\text{З}=\frac{v_\text{Р-С}+v_\text{С-З}}{1+\frac{v_\text{Р-С}\cdot v_\text{С-З}}{c^2}}, $$ де \(v_\text{З}\) ‒ проєкція швидкості руху ракети відносно Землі як нерухомої системи відліку, \(v_\text{Р-С}\) ‒ проєкція швидкості руху ракети відносно космічної станції як рухомої системи відліку, \(v_\text{С-З}\) ‒ проєкція швидкості руху рухомої системи відліку відносно нерухомої ‒ космічної станції відносно Землі, \(c\) ‒ швидкість поширення світла у вакуумі.

Відповідно до другого постулату СТВ швидкість поширення світла ‒ максимально можлива швидкість поширення будь-якої взаємодії. Матеріальні об’єкти не можуть мати швидкість більшу за швидкість світла. Отже, варіант відповіді Г \((1,7c)\) суперечить другому постулату СТВ і є неправильним.

Підставмо у формулу вирази, що відповідають швидкостям руху космічної станції відносно Землі і ракети відносно цієї станції. Звернімо увагу, що ця формула записана для випадку додавання швидкостей, напрямлених уздовж однієї прямої \((\text{осі}\ Ox),\) як це зображено на рисунку в умові завдання. Оскільки і ракета, і станція рухаються в один бік, то у формулі в чисельнику швидкості додаємо \((0,9c+0,8c).\)

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку вміння записувати рівняння ядерної реакції та визначати її результати.

Запишімо рівняння ядерної реакції, описаної в умові завдання: $$ \mathrm{^3_2He\ +\ ^3_1H\ \rightarrow\ ^4_2He\ +\ }^A_Z\mathrm{X}, $$ де \(\mathrm{X}\) ‒ невідома частинка, що утворилася внаслідок реакції.

У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь визначмо зарядове \(Z\) та масове \(A\) числа невідомого елемента \(\mathrm{X}.\)

Запишімо суму мас і суму зарядів для обох частин рівняння реакції: \begin{gather*} 3+3=4+A,\\[7pt] 2+1=2+Z. \end{gather*}

Із цих рівнянь маємо: \begin{gather*} A=2,\\[7pt] Z=1. \end{gather*}

Невідомий елемент \(^2_1\mathrm{X}\) ‒ це ізотоп Гідрогену Дейтерій \(^2_1\mathrm{H}.\)

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Утворення лінійчастого спектра.

Завдання скеровано на перевірку розуміння і застосування знань про спектральний аналіз речовин.

Кожен газ в атомарному стані дає власний набір ліній спектра (власний чітко визначений набір довжин хвиль). Ці лінії завжди розташовані в тих самих місцях спектра, незалежно від способу збудження атомів.

Лінійчастий спектр будь-якого хімічного елемента не збігається з лінійчастим спектром інших хімічних елементів, тож є своєрідною «візитівкою» атомів із тим самим зарядом ядра.

Порівняймо за рисунком, наведеним в умові завдання, лінії спектра зразка невідомої речовини зі спектрами випромінювання Стронцію і Кальцію. Усі лінії спектра Стронцію є в зразку невідомої речовини, а ліній спектра Кальцію немає. Отже, у невідомій речовині є атоми Стронцію, але немає атомів Кальцію.

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку вміння визначати напрямок рівнодійної сил і напрямок швидкості руху тіл під час різних видів руху.

Розгляньмо приклад A. Коли автобус гальмує, то рівнодійна \(\overrightarrow{F}\) усіх сил, що діють на автобус, буде напрямлена протилежно до напрямку руху, тобто до напрямку швидкості \(\overrightarrow{v}\) руху автобуса (див. рисунок). Отже, ситуації А відповідає опис 1 рівнодійної сил.

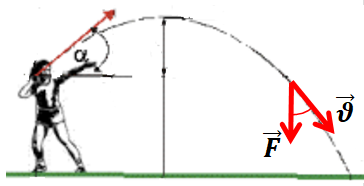
Коли футбольний м’яч, спрямований воротарем на іншу половину футбольного поля, піднімається, то рівнодійна \(\overrightarrow{F}\) усіх сил, що діють на м’яч, напрямлена вертикально вниз, а швидкість \(\overrightarrow{v}\) руху м’яча ‒ по дотичній до траєкторії руху м’яча вгору, тож кут між векторами \(\overrightarrow{F}\) і \(\overrightarrow{v}\) – тупий. Отже, жоден опис 1–4 не відповідає прикладу Б.

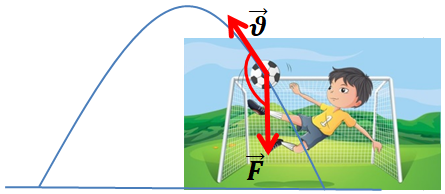
Напрямок рівнодійної \(\overrightarrow{F}\) усіх сил, що діють на снаряд, який рухається всередині ствола гармати під час пострілу, збігається з напрямком швидкості \(\overrightarrow{v}\) руху снаряда. Отже, прикладу B відповідає опис 2 рівнодійної сил.

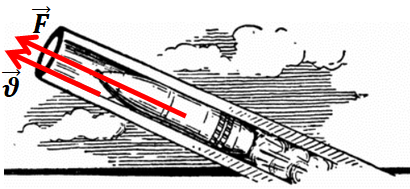
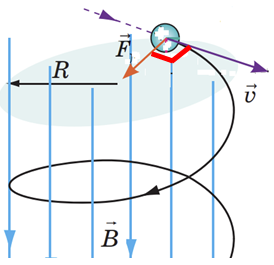
Коли електрон улітає в магнітне поле під певним кутом до ліній магнітної індукції, то траєкторією його руху є гвинтова лінія. Рівнодійна \(\overrightarrow{F}\) сил, що діють на електрон, буде напрямлена до центру витків гвинтової лінії, а швидкість \(\overrightarrow{v}\) руху електрона ‒ по дотичній до траєкторії руху, тому кут між векторами \(\overrightarrow{F}\) і \(\overrightarrow{v}\) прямий. Отже, Прикладу Г відповідає опис 3 рівнодійної сил.

У прикладі з падінням камінця, кинутого під кутом до горизонту, рівнодійна \(\overrightarrow{F}\) усіх сил, що діють на камінець, напрямлена вертикально вниз, а швидкість \(\overrightarrow{v}\) руху камінця ‒ по дотичній до його траєкторії руху вниз. Тобто кут між векторами \(\overrightarrow{F}\) і \(\overrightarrow{v}\) гострий. Прикладу Д відповідає опис 4 рівнодійної сил.

Відповідь: 1А, 2В, 3Г, 4Д.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси.

Завдання скеровано на перевірку розуміння ізопроцесів та їхньої графічної інтерпретації.

Розгляньмо ізохорний процес 1–2 \((V=const),\) за якого тиск \(p\) зростає (див. рисунок). Отже, відповідно до рівняння Клапейрона температура \(T\) теж зростатиме (стрілочка, напрямлена вгору, означає зростання значення величини): $$ \frac pT=const\Rightarrow \frac{p\uparrow}{T\uparrow}=const. $$ Отже, процес 1–2 ‒ це ізохорне нагрівання (Б).

Розгляньмо ізобарний процес 2‒3 \((p=const),\) за якого об’єм \(V\) збільшується (див. рисунок). Отже, відповідно до рівняння Клапейрона, температура \(T\) теж зростатиме: $$ \frac VT=const\Rightarrow\frac{V\uparrow}{T\uparrow}=const. $$ Отже, процес 2‒3 ‒ це ізобарне нагрівання (А).

Розгляньмо ізотермічний процес 3‒4 \((T=const),\) за якого тиск \(p\) падає, а об’єм \(V\) збільшується (див. рисунок). Відповідно до рівняння Клапейрона: $$ pV=const\Rightarrow p\downarrow V\uparrow = const. $$ Отже, процес 3‒4 ‒ це ізотермічне розширення (Г).

Розгляньмо ізобарний процес 4‒1 \((p=const),\) за якого об’єм \(V\) зменшується (див. рисунок). Отже, відповідно до рівняння Клапейрона температура \(T\) теж зменшуватиметься (стрілочка, напрямлена вниз, означає зменшення значення величини): $$ \frac VT=const\Rightarrow\frac{V\downarrow}{T\downarrow}=const. $$ Отже, процес 4‒1 ‒ це ізобарне охолодження (Д).

Відповідь: 1Б, 2А, 3Г, 4Д.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.

На взаємодії магнітного поля постійних магнітів компаса з горизонтальним складником магнітного поля Землі заснований принцип дії цього приладу. Вільно обертова магнітна стрілка повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного (Північного географічного) полюса.

Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічну дію електричного струму спостерігають під час проходження його крізь розчин електроліту в електролітичній ванні.

Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком. Один із наслідків електромагнітної індукції, практично важливий для генерації електричного струму, ‒ виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме генератори змінного струму (ГЗС) ‒ це джерела електричної енергії, які створюють електрорушійну силу (ЕРС), що періодично змінюється.

Робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача. Під час проходження електричного струму спіраль лампи розжарювання сильно нагрівається завдяки тепловій дії струму.

Будь-який напівпровідниковий діод складений із двох контактних напівпровідникових ділянок із різними типами провідності ‒ електронною і дірковою; до кожної ділянки приєднано виводи. Основна властивість напівпровідникового діода ‒ пропускати електричний струм переважно в одному напрямку.

Відповідь: 1Б, 2Г, 3А, 4В.

ТЕМА: Коливання і хвилі. Оптика.

Завдання скеровано на перевірку знання і розуміння явищ геометричної і хвильової оптики.

Заломлення ‒ це явище зміни напрямку поширення хвилі під час її проходження через плоску межу двох однорідних середовищ.

Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.

Дисперсія ‒ це явище залежності показника заломлення середовища від довжини електромагнітної хвилі.

Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігається стійка в часі картина посилення їх та послаблення в різних точках простору.

Відповідь: 1Б, 2Д, 3А, 4Г.

ТЕМА: Механіка. Основи динаміки. Закон всесвітнього тяжіння. Сила тяжіння. Рух штучних супутників. Перша космічна швидкість.

Завдання скеровано на перевірку розуміння і застосування закону всесвітнього тяжіння, а також розуміння руху штучних супутників.

1. Для того, щоб об’єкт рухався біля планети коловою орбітою, йому необхідно надати швидкість, яку називають першою космічною швидкістю.

Візьмемо до уваги, що саме сила тяжіння \(F_\text{тяж}\) надає тілу масою \(m\) доцентрового прискорення \(a_\text{доц}\) (див. рисунок).

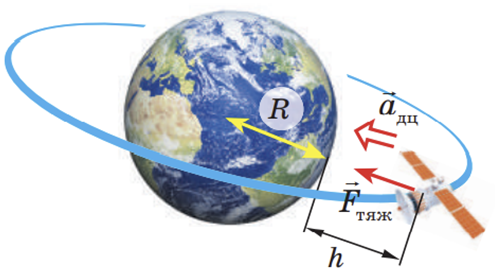
За другим законом Ньютона \(F_\text{тяж}=ma_\text{доц,}\) де за законом всесвітнього тяжіння $$ F_\text{тяж}=G\frac{mM}{(R + h)^2}, $$ отже, $$ a_\text{доц}=\frac{GM}{(R + h)^2} $$ (\(G\) ‒ гравітаційна стала, \(M\) ‒ маса планети, \(R\) ‒ радіус планети, \(h\) ‒ висота над поверхнею планети). Позначмо буквою \(r\) відстань від центра планети до супутника \((R+h)\) і запишімо формули для визначення доцентрового прискорення обох супутників: \begin{gather*} a_{1\text{доц}}=\frac{GM}{r^2_1},\\[6pt] a_{2\text{доц}}=\frac{GM}{r^2_2}. \end{gather*}

Обчислімо, у скільки разів прискорення руху першого супутника більше за прискорення руху другого супутника, урахувавши співвідношення їхніх радіусів: $$ \frac{a_{1\text{доц}}}{a_{2\text{доц}}}=\frac{GM}{r_1^2}:\frac{GM}{r^2_2}=\frac{GM\cdot 16r^2_1}{r^2_1\cdot GM}=16. $$

Отже, \(a_\text{1доц}\gt a_\text{2доц}\) у \(16\) разів.
Відповідь: 16.

2. Формули для обчислення перших космічних швидкостей руху супутників виведемо з формул для їхніх доцентрових прискорень: \begin{gather*} a_\text{1доц}=\frac{v^2_1}{r_1}\Rightarrow v^2_1=a_\text{1доц}\cdot r_1,\\[6pt] a_\text{2доц}=\frac{v^2_2}{r_2}\Rightarrow v^2_2=a_\text{2доц}\cdot r_2. \end{gather*}

Обчислімо, у скільки разів швидкість \(v_1\) руху першого супутника більша за швидкість \(v_2\) руху другого супутника:

Отже, \(v_1\gt v_2\) у \(2\) рази.
Відповідь: 2.

Відповідь: 1. 16. 2. 2.

ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора. Енергія електричного поля.

Завдання скеровано на перевірку знання і застосування формул для обчислення електроємності плоского конденсатора й енергії електричного поля конденсатора.

1. Конденсатор, складений із двох паралельних металевих пластин (обкладок), розділених шаром діелектрика, називають плоским. Електроємність \(C\) плоского конденсатора обчислюють за формулою $$ C=\frac{\varepsilon_0\varepsilon S}{d}, $$ де \(\varepsilon_0\) ‒ електрична стала; \(\varepsilon\) ‒ діелектрична проникність діелектрика; \(S\) ‒ площа пластини конденсатора; \(d\) ‒ відстань між пластинами.

Підставмо у формулу значення величин, виражених у системі СІ, й обчислімо електроємність конденсатора:

Відповідь: 45.

2. Заряджений конденсатор має енергію. Цю енергію точніше було б назвати енергією електростатичного поля, яке існує між обкладками зарядженого конденсатора, оскільки енергія будь-яких заряджених тіл зосереджена в електричному полі, створюваному цими тілами.

Отже, обчислімо енергію \(W,\) що виділиться під час розряджання конденсатора. Вона дорівнює половині добутку електроємності \(C\) і квадрата напруги \(U\) на конденсаторі:

Відповідь: 36.

Відповідь: 1. 45. 2. 36.

ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Закон збереження енергії в механічних процесах.

Завдання скеровано на перевірку вміння застосовувати закон збереження механічної енергії під час розв’язування задач про рух тіла під дією кількох сил.

Якщо тілу надати певної швидкості, то воно матиме кінетичну енергію \(E_\mathrm{k}.\) Цієї енергії повинно вистачити, щоб тіло змогло піднятися вздовж похилої площини (кінетична енергія перейде в потенціальну енергію \(E_\mathrm{p}\)), долаючи під час цього силу тертя ковзання. Запишімо закон збереження механічної енергії для руху: $$ E_\mathrm{k}-A=E_\mathrm{p}, $$ де \(A\) ‒ робота сили тертя ковзання, яка є від’ємною, тому що напрямок сили тертя ковзання протилежний до напрямку руху тіла. Робота сили тертя ковзання дорівнює добутку модуля сили тертя ковзання \(F_\text{тер ковз}\) і модуля переміщення \(l\) (де \(l\) ‒ довжина дошки): $$ A=F_\text{тер ковз}\cdot l=\mathbf{\mu}N\cdot l=\mathbf{\mu}mg\cos\mathbf{\alpha}\cdot l, $$ де \(\mathbf{\mu}\) ‒ коефіцієнт тертя, \(N\) ‒ модуль сили нормальної реакції опори, \(m\) ‒ маса тіла, \(g\) ‒ прискорення вільного падіння, \(\mathbf{\alpha}\) ‒ кут нахилу похилої площини (під час руху похилою площиною сила нормальної реакції опори дорівнює проєкції сили тяжіння на вісь \(Oy\)). Щоб унаочнити умову завдання і дібрати спосіб розв’язання, скористаймося схематичним рисунком.

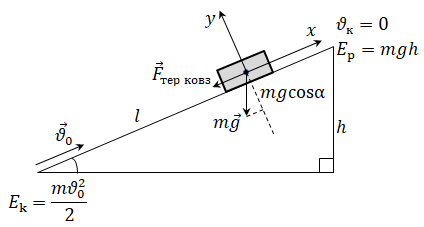
Отже,

Відповідь: 6.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку вміння складати рівняння теплового балансу.

Запишімо в загальному вигляді рівняння теплового балансу:

де \(n\) – кількість тіл, що віддають енергію; \(k\) – кількість тіл, що отримують енергію. Формулюють його так: в ізольованій системі тіл, у якій внутрішня енергія тіл змінюється лише внаслідок теплопередачі, загальна кількість теплоти, віддана одними тілами системи, дорівнює загальній кількості теплоти, отриманої іншими тілами цієї системи.

Запишімо рівняння теплового балансу відповідно до умови завдання, де гаряча вода віддає певну кількість теплоти \(Q_\text{г}\) холодній воді, відповідно холодна вода таку саму кількість теплоти \(Q_\text{х}\) отримає: \begin{gather*} Q_\text{г}^-=Q_\text{х}^+,\\[7pt] Q_\text{г}=cm_\text{г}(t_\text{г}-t_\text{к}), \end{gather*} де \(c\) ‒ питома теплоємність води, \(m_\text{г}\) ‒ маса гарячої води, \(t_\text{г}\) ‒ початкова температура гарячої води, \(t_\text{к}\) ‒ кінцева температура води, що встановилася в калориметрі: $$ Q_\text{х}=cm_\text{х}(t_\text{к}-t_\text{х}), $$ де \(c\) ‒ питома теплоємність води, \(m_\text{х}\) ‒ маса холодної води, \(t_\text{х}\) ‒ початкова температура холодної води, \(t_\text{к}\) ‒ кінцева температура води, що встановилася в калориметрі:

Відповідь: 64.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та вимірювання її.

Завдання скеровано на перевірку розуміння і застосування формул абсолютної і відносної вологості.

Відносна вологість \(\mathbf{\varphi}\) ‒ фізична величина, якою характеризують ступінь насиченості водяної пари. Вона дорівнює відношенню абсолютної вологості \(\mathbf{\rho}_\text{а}\) до густини \(\mathbf{\rho}_\text{н.п.}\) насиченої водяної пари за певної температури. Зазвичай відносну вологість подають у відсотках: $$ \mathbf{\varphi}=\frac{\mathbf{\rho}_\text{а}}{\mathbf{\rho}_\text{н.п.}}\cdot 100\ \text{%} $$

Абсолютна вологість \(\mathbf{\rho}_\text{а}\) ‒ фізична величина, якою характеризують уміст водяної пари в повітрі. Абсолютна вологість чисельно дорівнює масі \(m_{\mathrm{Н_2О}}\) водяної пари, що міститься в повітрі об’ємом \(V=1\ \text{м}^3:\) $$ \mathbf{\rho}_\text{а}=\frac{m_{\mathrm{Н_2О}}}{V}. $$

Запишімо формули відносної вологості \(\mathbf{\varphi}_1\) і \(\mathbf{\varphi}_2\) окремо для кожної кімнати до і після того, як між кімнатами розчахнули двері \((\mathbf{\varphi}):\)

де \(m_1\) і \(m_2\) ‒ маса води в першій і другій кімнатах відповідно, \(V_1\) і \(V_2\) ‒ об’єми першої і другої кімнати відповідно.

За умовою завдання температура повітря в кімнатах була однакова і не змінилася після розчахування дверей. Це означає, що густина \(\mathbf{\rho}_\text{н.п.}\) насиченої водяної пари за цієї температури ‒ величина незмінна.

Виразімо маси \(m_1\) і \(m_2\) з формул відносної вологості для окремих кімнат, і підставимо ці вирази у формулу загальної вологості після розчахування дверей:

Відповідь: 72.

ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона. Механіка. Основи динаміки. Рух тіл під дією кількох сил.

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі з різних розділів фізики.

Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат для початкового стану: \begin{gather*} m\overrightarrow{a}=m\overrightarrow{g}+\overrightarrow{T}+\overrightarrow{F}_\text{K},\\[6pt] Ox:\ \ \ 0=-T\sin\frac{\mathbf{\alpha}}{2}+F_\text{K},\\[6pt] Oy:\ \ \ 0=-mg+T\cos\frac{\mathbf{\alpha}}{2}, \end{gather*} де \(m\) ‒ маса кульки, \(\overrightarrow{a}\) ‒ прискорення руху кульки, \(\overrightarrow{g}\) ‒ прискорення вільного падіння, \(\overrightarrow{T}\) ‒ сила натягу нитки, \(\overrightarrow{F}_\text{K}\) ‒ сила Кулона.

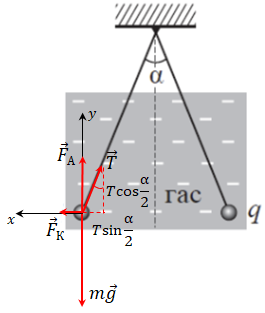
Дістаємо систему рівнянь: $$ \left\{ \begin{array}{l} T=\frac{F_\text{K}}{\sin\frac{\mathbf{\alpha}}{2}}\\ mg=T\cos\frac{\mathbf{\alpha}}{2} \end{array} \right. $$

Звідси \begin{gather*} mg=\frac{F_\text{K}\cos\frac{\mathbf{\alpha}}{2}}{\sin\frac{\mathbf{\alpha}}{2}}=F_\text{K}\operatorname{ctg}\frac{\mathbf{\alpha}}{2}. \end{gather*}

Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат, коли кульки занурили в гас: \begin{gather*} m\overrightarrow{a}=m\overrightarrow{g}+\overrightarrow{F}_\text{А}+\overrightarrow{T}_\text{г}+\overrightarrow{F}_\text{гК},\\[6pt] Ox:\ \ \ 0=-\overrightarrow{T}_\text{г}\sin\frac{\mathbf{\alpha}}{2}+\frac{F_\text{K}}{\mathbf{\varepsilon}},\\[6pt] Oy:\ \ \ 0=-mg+F_\text{А}+T_\text{г}\cos\frac{\mathbf{\alpha}}{2}, \end{gather*} де \(\overrightarrow{T}_\text{г}\) ‒ сила натягу нитки в гасі, \(\overrightarrow{F}_\text{гК}\) ‒ сила Кулона, що діє між кульками в гасі, \(\mathbf{\varepsilon}\) ‒ діелектрична проникність гасу, \(\overrightarrow{F}_\text{А}\) ‒ сила Архімеда.

Сила Кулона в гасі зміниться від того, що в іншого середовища інша діелектрична проникність. За умовою кут між нитками не змінився після занурення в гас. Тож відстань між кульками не змінилася. Але на кульки в гасі діє сила Архімеда. Узявши до уваги всі ці умови, дістаємо систему рівнянь: $$ \left\{ \begin{array}{l} T_\text{г}=\frac{F_\text{K}}{\mathbf{\varepsilon}\cdot \sin\frac{\mathbf{\alpha}}{2}}\\ mg=F_\text{А}+T_\text{г}\cos\frac{\mathbf{\alpha}}{2} \end{array} \right. $$

Звідси

Складімо систему з отриманих для обох ситуацій рівнянь і розв’яжімо її:

де \(\mathbf{\rho}_\text{к}\) ‒ густина матеріалу кульок, \(V_\text{к}\) ‒ об’єм кульки, \(\mathbf{\rho}_\text{г}\) ‒ густина гасу.

Тобто \begin{gather*} \mathbf{\rho}_\text{к}=\mathbf{\rho}_\text{г}+\frac{\mathbf{\rho}_\text{к}}{\mathbf{\varepsilon}},\\[6pt] \mathbf{\rho}_\text{к}=\frac{\mathbf{\rho}_\text{г}}{1-\frac{1}{\mathbf{\varepsilon}}}\\[6pt] \mathbf{\rho}_\text{к}=\frac{800\ \text{кг/м}^3}{1-\frac 12}=1600\ \text{кг/м}^3. \end{gather*}

Відповідь: 1600.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Закон електромагнітної індукції.

Завдання скеровано на перевірку розуміння закону електромагнітної індукції.

Силу індукційного струму \(I_\text{i}\) в контурі опором R визначають за законом Ома: $$ I_\text{i}=\frac{\mathbf{\varepsilon}_\text{i}}{R}. $$

Закон залежності електрорушійної сили \(\mathbf{\varepsilon}_\text{i}\) (ЕРС) індукції від швидкості зміни магнітного потоку експериментально вивів М. Фарадей: електрорушійна сила індукції дорівнює швидкості зміни магнітного потоку, який пронизує поверхню, обмежену контуром: $$ \mathbf{\varepsilon}_\text{i}=-\frac{\Delta\mathrm{\text{Ф}}}{\Delta t}, $$ де \(\Delta\mathrm{\text{Ф}}\) ‒ зміна магнітного потоку, \(\Delta t\) ‒ проміжок часу (знак «мінус» відображає правило Ленца).

Оскільки за умовою змінюється площа, обмежена контуром, маємо: $$ \mathbf{\varepsilon}_\text{i}=B\frac{\Delta S}{\Delta t}\cos\mathbf{\alpha}, $$ де \(B\) ‒ індукція магнітного поля, \(\Delta S\) ‒ зміна площі, обмеженої контуром.

За умовою завдання провідник постійно перебуває в горизонтальній площині перпендикулярно до ліній індукції магнітного поля. Це означає, що лінії індукції магнітного поля паралельні з нормаллю до площини поверхні контуру, тобто кут \(\mathbf{\alpha}\) між ними дорівнює нулю, \(\cos\ 0^\circ=1,\) тоді $$ \mathbf{\varepsilon}_\text{i}=B\frac{\Delta S}{\Delta t}. $$

Розпишімо, чому дорівнює сила струму й опір, і підставимо всі вирази в першу формулу:

де \(q\) ‒ електричний заряд, що пройде через поперечний переріз провідника за час \(\Delta t,\ \ \mathbf{\rho}\) ‒ питомий опір провідника, \(l\) ‒ довжина провідника, \(S_\text{пп}\) ‒ площа поперечного перерізу провідника.

Визначмо зміну площі \(\Delta S\) обмеженої контуром, що дорівнює різниці площі круга \(S_\text{к}\) і площі квадрата \(S_\text{кв},\) обмежених тим самим провідником довжиною \(l:\) $$ \Delta S=S_\text{к}-S_\text{кв}. $$

Довжина кола \(l=2\mathbf{\pi}r,\) де \(r\) ‒ радіус кола. Отже, площа круга, обмежена цим колом, дорівнюватиме $$ S_\text{к}=\mathbf{\pi}r^2=\frac{\mathbf{\pi}l^2}{4\mathbf{\pi}^2}=\frac{l^2}{4\mathbf{\pi}}. $$

Якщо з провідника довжиною \(l\) утворити квадрат, то сторона квадрата дорівнює \(\frac l4,\) а площа \begin{gather*} S_\text{кв}=\left(\frac{l}{4}\right)^2=\frac{l^2}{16}.\\[6pt] \Delta S=S_\text{к}-S_\text{кв}=\frac{l^2}{4\mathbf{\pi}}-\frac{l^2}{16}=l^2\left(\frac{4-\mathbf{\pi}}{16\mathbf{\pi}}\right). \end{gather*}

Обчислімо шукану величину:

Відповідь: 62,5.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Власна частота й період електромагнітних коливань. Формула Томсона.

Завдання скеровано на перевірку розуміння принципу дії коливального контуру.

Електромагнітну хвилю характеризують довжиною \(\mathbf{\lambda},\) частотою \(\mathbf{\nu}\) (періодом \(T\)) і швидкістю \(c\) поширення у вакуумі: $$ \mathbf{\lambda}=\frac{c}{\mathbf{\nu}}=cT. $$

Для того, щоб коливальний контур міг уловити випромінювані хвилі, його треба настроїти на частоту коливань випромінювача. Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.

Ураховуючи, що коливальний контур настроєний на таку саму частоту, із якою поширюється хвиля, і що частота і період взаємно обернені величини, дістанемо формулу для обчислення електроємності: \begin{gather*} \mathbf{\lambda}=cT=c2\mathbf{\pi}\sqrt{LC},\\[6pt] C=\frac{\mathbf{\lambda}^2}{c^2 4\mathbf{\pi}^2\cdot L}. \end{gather*}

Оскільки електроємність прямо пропорційна квадрату довжини хвилі, то електроємність конденсатора буде максимальною за максимального значення довжини хвилі, на яку може налаштуватися коливальний контур: \begin{gather*} C=\frac{540^2}{9\cdot 10^{16}\ \left(\frac{\text{м}}{\text{с}}\right)^2\cdot 4\cdot 10\cdot 0,27\cdot 10^{-3}\ \text{Гн}}=\\[6pt] =\frac{3}{10^{10}}\ \text{Ф}=300\cdot 10^{-12}\ \text{Ф}=300\ \text{пФ}. \end{gather*}

Відповідь: 300.

ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.

Завдання скеровано на перевірку розуміння поширення світла в різних середовищах.

Фізичну величину, якою характеризують оптичну густину середовища, і яка показує, у скільки разів швидкість \(v\) поширення світла в середовищі менша, ніж швидкість \(c\) поширення світла у вакуумі, називають абсолютним показником заломлення середовища \(n:\) $$ n=\frac cv. $$

Звідси $$ v=\frac cn. $$

За умовою завдання час \(t_\text{в}\) поширення світла у вакуумі той самий, що й у склі \(t_\text{ск}:\) \begin{gather*} t_\text{ск}=t_\text{в},\\[6pt] t_\text{ск}=\frac{l_\text{ск}}{v},\\[6pt] t_\text{в}=\frac{l_\text{в}}{c}, \end{gather*} де \(l_\text{ск}\) ‒ відстань, яку пройшло світло у склі, \(l_\text{в}\) ‒ відстань, яку пройшло світло у вакуумі.

\begin{gather*} \frac{l_\text{ск}}{v}=\frac{l_\text{в}}{c},\\[6pt] l_\text{в}=\frac{l_\text{ск}c}{v}=\frac{l_\text{ск}cn}{c}=l_\text{ск}n,\\[6pt] l_\text{в}=10\ \text{м}\cdot 1,6=16\ \text{м}. \end{gather*}

Відповідь: 16.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи формули, що описують кванти світла (фотони).

За умовою завдання імпульс електрона \(p_\text{е}\) дорівнює імпульсу фотона \(p_\text{ф}\) світла, від якого електрон отримує енергію: $$ p_\text{е}=p_\text{ф}. $$

Імпульс фотона дорівнює відношенню сталої Планка \(h\) до довжині хвилі \(\mathbf{\lambda}\) фотона: $$ p_\text{ф}=\frac{h}{\mathbf{\lambda}}. $$

Імпульс електрона дорівнює добутку маси \(m_\text{е}\) електрона і швидкості \(v_\text{е}\) його руху: $$ p_\text{е}=m_\text{е}\cdot v_\text{е}. $$

Обчислімо швидкість руху електрона:

Відповідь: 1,1.