ЗНО онлайн 2017 року з фізики – основна сесія

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з додавання швидкостей.

Вважатимемо першу систему відліку нерухомою, а другу – рухомою. Швидкість тіла в рухомій системі відліку можна визначити за формулою: $$ \overrightarrow{V_{\text{тіла рух}}}=\overrightarrow{V_{\text{тіла нерух}}}+\overrightarrow{V_{\text{рух}}}, $$ де \(\overrightarrow{V_{\text{тіла рух}}}\) – швидкість тіла в рухомій системі відліку, \(\overrightarrow{V_{\text{тіла нерух}}}\) – швидкість тіла в нерухомій системі відліку, \(\overrightarrow{V_{\text{рух}}}\) – швидкість рухомої системи відліку.

Тоді швидкість рухомої системи можна визначити за формулою $$ \overrightarrow{V_{\text{рух}}}=\overrightarrow{V_{\text{тіла рух}}}-\overrightarrow{V_{\text{тіла нерух}}}. $$

Найменшою буде швидкість рухомої системи відліку, якщо напрямок її руху збігається з напрямком руху самого тіла. Тоді векторне рівняння можна спроєктувати на вісь \(OX\):

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням законів Ньютона.

Дії сил на брусок зображено на рисунку 1. На нього діють сила тяжіння, сила реакції опори й сила тертя.

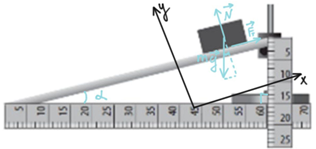
Рис. 1. Дії сил на брусок

Запис другого закону Ньютона для бруска: $$ m\overrightarrow{a}=\overrightarrow{N}+\overrightarrow{F_{\text{тяж}}}+\overrightarrow{F_{\text{тер}}}, $$ де \(m\) – маса бруска, \(a\) – прискорення тіла, \(N\) – сила реакції опори, \(F_{\text{тяж}}\) – сила тяжіння, \(F_{\text{тер}}\) – сила тертя.

Силу тяжіння і силу тертя можна визначити за такими формулами:

де \(\mathbf{\mu}\) – коефіцієнт тертя, \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Оскільки брусок ковзає рівномірно, то його прискорення дорівнює \(0\). Тоді другий закон Ньютона можна спроєктувати на осі \(OX\) та \(OY\):

Тоді

Коефіцієнт тертя можна обчислити за формулою $$ \mathbf{\mu}=\frac{mg\sin\mathbf{\alpha}}{mg\cos\mathbf{\alpha}}=\frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}=\operatorname{tg}\mathbf{\alpha}. $$

Можна визначити \(\operatorname{tg}\mathbf{\alpha}\) з прямокутного трикутника похилої площини. У ньому протилежний катет \(1=15\ \text{см}=0,15\ \text{м}\), а прилеглий катет \(b=60\ \text{см}=0,6\ \text{м}\). Тож $$ \mathbf{\mu}=\operatorname{tg}\mathbf{\alpha}=\frac ab=\frac{0,15\ \text{м}}{0,6\ \text{м}}=0,25. $$

Відповідь: A.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку розуміння відмінності між поняттями імпульсу тіла й імпульсу сили.

Імпульс тіла \((p_\text{тіла})\) пов’язаний з імпульсом сили, що на нього діє \((p_\text{сили})\): $$ p_\text{сили}=\Delta p_\text{тіла}=p_\text{тіла}-p_\text{тіла 0}. $$

Імпульс сили й імпульс тіла можна визначити за такими формулами: \begin{gather*} \overrightarrow{p_\text{сили}}=\overrightarrow{F}t,\\[7pt] \overrightarrow{p_\text{тіла}}=m\overrightarrow{v}, \end{gather*} де \(F\) – сила, що діє на тіло, \(t\) – час, упродовж якого діє сила, \(m\) – маса тіла, \(v\) – швидкість тіла.

Імпульс тіла залежить від часу:

Цим рівнянням описано пряму. Загальне рівняння прямої таке: $$ y=kx+b, $$ де \(k\) – кутовий коефіцієнт, що визначає нахил прямої, \(b\) – коефіцієнт, що визначає точку перетину з віссю \(OY\).

Для залежності \(p_\text{тіла}\) від часу \(tk=F\). Що більший кутовий коефіцієнт, то крутіший нахил прямої, тож \(F_1\gt F_3\).

Якщо кутовий коефіцієнт дорівнює нулю, то пряма є паралельною осі \(OX\), тому \(F_2=0\).

Відповідь: Б.

ТЕМА: Елементи механіки рідин і газів. Гідростатичний тиск.

Завдання скеровано на перевірку вміння визначати гідростатичний тиск.

Рівень рідини в трубці встановлюється так, що тиск у рідині на кожному рівні дорівнює тиску в рідині в широкій посудині.

Тиск у широкій посудині на кожному рівні можна визначити за формулою $$ p=p_\text{атм}+p_\text{гідр}, $$ де \(p_\text{гідр}\) – гідростатичний тиск, \(p_\text{атм}\) – атмосферний тиск.

Гідростатичний тиск – тиск нерухомого стовпчика рідини або газу.

Гідростатичний тиск визначають за формулою $$ p_\text{гідр}=\mathbf{\rho}gh $$ де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Тиск повітря в трубці можна вважати однаковим у кожній точці, уключно із тиском на межі повітря – рідина. Тиск на цій межі можна визначити за формулою $$ p=p_\text{атм}+p_\text{гідр}=p_\text{атм}+\mathbf{\rho}ga. $$

Відповідь: A.

ТЕМА: Молекулярна фізика та термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння стану ідеального газу.

Тиск, об’єм і температура ідеального газу пов’язані рівнянням стану ідеального газу $$ pV=nRT=\frac mM RT, $$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

Температуру газу можна визначити за формулою $$ T=pV=\frac{M}{mR}. $$

Значення тиску й об’єму для всіх станів, зображених на графіку такі (в умовних одиницях):

Тоді температури в кожному стані в умовних одиницях дорівнюватимуть:

З-поміж них вибираємо \(T_2=T_5\).

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку розуміння принципів теплообміну.

За першим законом термодинаміки кількість теплоти \(Q\), передана системі, іде на зміну внутрішньої енергії системи \((\Delta U)\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=A+\Delta U. $$

Зміна внутрішньої енергії пов’язана зі зміною температури речовини, що не змінює свого агрегатного стану: що вища температура речовини, то вища її внутрішня енергія. Тож, якщо температура речовини не змінюється, то і внутрішня енергія тіл також не змінюється: $$ Q=A. $$

Проте під час зміни агрегатного стану (фазового переходу) температура речовини не змінюється, а внутрішня енергія – змінюється. Наприклад, під час плавлення льоду він поглинає тепло, проте його температура не почне зростати доти, доки триває плавлення (фазовий перехід).

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка.

Завдання скеровано на перевірку розуміння поняття теплової рівноваги.

Стан теплової рівноваги – це такий стан макроскопічної системи, коли всі її макроскопічні параметри залишаються незмінними як завгодно довго.

Відповідь: Б.

ТЕМА: Властивості газів, рідин і твердих тіл. Насичена й ненасичена пара.

Завдання скеровано на перевірку розуміння особливостей температурних залежностей насиченої пари.

Тиск, об’єм і температура газу, який можна вважати ідеальним, пов’язані формулою $$pV=nRT,$$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура.

Формула залежності тиску \(p\) від температури \(T\) така: $$p=\frac{nR}{V}T.$$

Оскільки об’єм посудини незмінний, то ця формула описує пряму. Графік залежності в початковому стані не є графіком прямої, тож в посудині не може бути просто газ.

Насичена пара – це пара, яка перебуває в стані динамічної рівноваги зі своєю рідиною. Тож насичена пара не може існувати без рідини в тій самій посудині.

Під час підвищення температури посудини, у якій перебуває рідина й насичена пара, підвищується інтенсивність випаровування. Відповідно концентрація молекул рідини в повітрі збільшується. Тиск насиченої пари в такому разі зростає і внаслідок підвищення температури (за тим же принципом, що й тиск ідеального газу), і завдяки збільшенню концентрації молекул. Тобто тиск зростає швидше, ніж для ідеального газу. Коли рідина повністю випаровується, концентрація молекул рідини в повітрі не може збільшуватися, далі тиск зростає з тою самою залежністю, що й для ідеального газу.

Відповідь: В.

ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.

Завдання скеровано на оцінку вміння обчислювати напруженість електричного поля точкового заряду.

Напруженість поля точкового заряду можна визначити за формулою $$ E=k\frac{|Q|}{r^2}, $$ де \(Q\) – заряд, \(k\) – коефіцієнт пропорційності, \(r\) – відстань від заряду до точки вимірювання.

Якщо \(r_1=10\ \text{см}=0,1\ \text{м},\ r_2=5\ \text{см}=0,05\ \text{м}\), то

Відповідно $$ E_2=4E. $$

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Паралельне і послідовне з’єднання провідників.

Завдання скеровано на перевірку знання закону Ома й розуміння особливостей паралельного і послідовного з’єднання провідників.

Закони послідовного і паралельного з’єднання провідників схематично зображено на рисунках 1 і 2 відповідно.

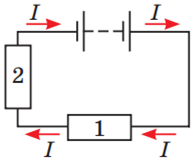
Рис. 1. Послідовне з’єднання провідників 1 і 2

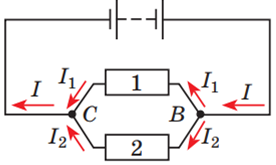
Рис. 2. Паралельне з’єднання провідників 1 і 2

З кількох резисторів номіналом \(12\ \text{кОм}\) не можна отримати систему з опором \(16\ \text{кОм}\) за допомогою послідовного з’єднання. До резистора з опором \(12\ \text{кОм}\) треба підключити систему резисторів з опором \(4\ \text{кОм}\).

Щоб отримати необхідні додаткові \(4\ \text{кОм}\), резистори мають бути з’єднані паралельно. Оскільки резистори однакові, то $$ \frac 1R=\frac{n}{R_n}, $$ де \(n\) – кількість резисторів, \(R=4\ \text{кОм}=4\ 000\ \text{Ом}\), а \(R_n=12\ \text{кОм}=12\ 000\ \text{Ом}\).

Відповідно $$ n=\frac{R_n}{R}=\frac{12000\ \text{Ом}}{4000\ \text{Ом}}=3. $$

Для заміни резистора опором \(16\ \text{кОм}\) потрібно \(3\) резистори, з’єднані паралельно, й один, підключений до них послідовно.

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота і потужність електричного струму.

Завдання скероване на перевірку вміння розв’язувати розрахункові задачі, що стосуються впливу змін напруги на потужність електричного струму.

Потужність струму в лампочках можна визначити за формулою: $$ P=UI, $$ де \(U\) – напруга, \(I\) – сила струму.

Оскільки опір ламп не змінюється, то потужність доцільно виразити через напругу й опір. Сила струму, напруга й опір пов’язані між собою законом Ома: $$ I=\frac UR. $$

Тож

Тоді

Відповідь: Г.

ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку вміння визначати напрямок дії сили Лоренца на заряджену частинку в магнітному полі.

Силу Лоренца визначають за правилом лівої руки: якщо ліву руку розташувати так, щоби лінії магнітної індукції входили в долоню, а чотири витягнуті пальці вказували напрямок швидкості руху позитивно зарядженої частинки, то відігнутий на \(90^\circ\) великий палець укаже напрямок сили Лоренца.

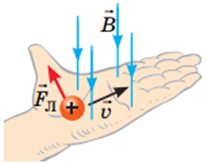
Рис. 1. Правило лівої руки

Якщо перевірити напрямок сили Лоренца на рисунку за правилом лівої руки, то великий палець вказуватиме праворуч, хоча на рисунку напрямок сили Лоренца вказаний ліворуч. Це свідчить про те, що частинка заряджена негативно.

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.

Завдання скеровано на перевірку розуміння явища магнітної індукції.

Рух магніту крізь кільце викликає в ньому появу індукційного струму. Індукційний струм у кільці виникає такий, щоб утворене навколо нього магнітне поле протидіяло рухові магніту. Тобто якщо магніт наближається до кільця, то навколо кільця утвориться поле, що примушуватиме його віддалятись і навпаки.

Напрямок магнітного поля можна визначити за правилом правої руки (рис. 1):
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму в контурі, то відігнутий на \(90^\circ\) великий палець укаже напрямок ліній магнітної індукції магнітного поля всередині контуру.

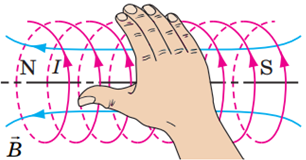
Рис. 1. Правило правої руки

Тоді для варіантів відповіді А – В північний полюс кільця буде розташований над ним, а південний – під ним. У варіанті Г навпаки – північний полюс котушки відштовхуватиме північний полюс магніту або притягувати його південний полюс. Ці дії спрямовані на те, щоби не дати північному полюсу магніту наблизитися або південному – віддалитися. Цю умову задовольняє лише варіант А.

Відповідь: A.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на перевірку розуміння основних величин, пов’язаних із коливаннями математичного маятника.

Відхилене на невелику відстань від вертикального положення масивне тіло на довгій нерозтяжній нитці можна вважати математичним маятником.

Оскільки радіуси сталевої та дерев’яної кульок однакові, то їхні об’єми рівні. Однак густина сталі більша за густину деревини, тому сталева кулька масивніша за дерев’яну.

Період коливань математичного маятника можна визначити за формулою $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) – довжина маятника; \(g\) – прискорення вільного падіння.

Від маси кульки період не залежить, тож він буде однаковим для обох маятників.

Коливання з більшою енергією згасатимуть повільніше. Енергію коливань можна визначити як потенціальну енергію в момент початку коливань. Потенціальну енергію тіла, піднятого над поверхнею Землі можна визначити за формулою $$ E=mgh, $$ де \(m\) – маса тіла, \(h\) – висота підйому.

Оскільки обидві кульки відвели на однакову відстань, то й висота їхнього підйому теж буде однаковою. Тоді кулька з більшою масою – сталева – матиме більшу енергію порівняно з дерев’яною. Тому коливання сталевої кульки згасатимуть повільніше.

Відповідь: Г.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на перевірку розуміння поняття амплітуди коливань.

Амплітуда коливань – це максимальне відхилення від положення рівноваги. За одне коливання тіло проходить відстань, яка дорівнює чотирьом амплітудам (рис. 1).

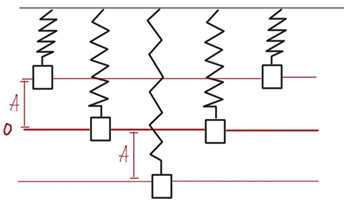
Рис. 1. Одне повне коливання пружинного маятника

Тоді за п’ять коливань тіло проходить \(5\cdot 4\cdot 0,5\ \text{м}=10\ \text{м}\).

Відповідь: A.

ТЕМА: Природні явища.

Завдання скеровано на перевірку вміння поєднувати фізичні явища з їхніми проявами в природі й використанням у техніці.

Явище, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини, називають явищем повного внутрішнього відбивання.

А Сонячне затемнення – це явище, під час якого Місяць відкидає повну тінь на поверхню Землі.

Б Крила метелика складені з хітинових лусочок, які утворюють дифракційну ґратку.

В Веселка – це наслідок дисперсії сонячного світла на краплинках води в повітрі.

Г Світло поширюється у світловоді завдяки повному внутрішньому відбиванню, адже оптична густина скла більша за оптичну густину повітря зовні.

Відповідь: Г.

ТЕМА: Оптика. Лінза. Оптична сила лінзи.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з оптики на основі аналізу оптичних схем.

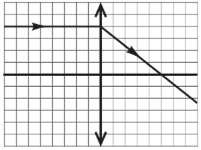
Рис. 1. Умова завдання

Промені, паралельні головній оптичній осі, збираються у фокусі збиральної лінзи. За рисунком 1 фокусна відстань \(F\) становить п’ять клітинок. Оскільки відстань між лініями сітки дорівнює \(2\ \text{см}\), то $$ F=2\cdot 5\ \text{см}=10\ \text{см}=0,1\ \text{м}. $$

Оптичну силу лінзи можна визначити за формулою $$ D=\frac 1F=\frac{1}{0,1\ \text{м}}=10\ \text{дптр} . $$

Відповідь: Г.

ТЕМА: Квантова фізика. Атом та атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку розуміння поняття енергетичного виходу реакції.

Енергетичним виходом ядерної реакції називають різницю енергій спокою ядер і частинок до і після реакції:

Відповідь: Б.

ТЕМА: Квантова фізика. Атом та атомне ядро. Радіоактивність.

Завдання скеровано на перевірку розуміння природи радіоактивного випромінювання.

Ернест Резерфорд виявив, що під дією магнітного поля пучок радіоактивного випромінювання ділиться на три частини (рис. 1).

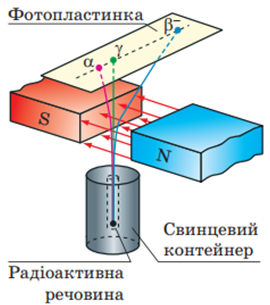
Рис. 1. Дослідження явища радіоактивності методом відхилення променів у магнітному полі

Поділ відбувається тому, що під дією магнітного поля заряджені частинки відхиляються від своєї початкової прямолінійної траєкторії завдяки дії сили Лоренца.

Нейтральний γ-промінь не відхилявся під дією магнітного поля, натомість позитивно заряджені α-частинки й негативно заряджені β-частинки відхилялися та утворювали два пучки по обидва боки обабіч пучка γ-променів. Адже різнойменно заряджені частинки в магнітному полі відхиляються в протилежні боки.

Відповідь: B.

ТЕМА: Механіка. Динаміка. Капілярні явища. Сила Архімеда. Сила пружності. Невагомість.

Завдання скеровано на перевірку розуміння природи фізичних явищ і сил.

1 Капілярні явища зумовлені тим, що рідини в тонких трубках мають велику площу контактування з твердою речовиною. Увігнутий або опуклий меніск утворюється залежно від того, чи змочує рідина поверхню чи не змочує. Унаслідок дії сил поверхневого натягу під деформованою поверхнею виникне надлишковий тиск (тиск Лапласа), який приведе до підняття або опускання стовпчика рідини.

2 Архімедова сила виникає завдяки тому, що в однорідних рідинах на різних рівнях установлюється різний гідростатичний тиск. Що більша глибина, то більший гідростатичний тиск. За законом Паскаля тиск у рідинах і газах поширюється однаково в усіх напрямках. Тоді на верхню поверхню тіла діє менший порівняно з нижньою його поверхнею тиск. Унаслідок такої різниці тисків утворюється сила, що завжди спрямована на виштовхування тіла з рідини – сила Архімеда.

3 Сила пружності – це сила, яка виникає під час деформації тіла й намагається повернути тіло в недеформований стан.

4 Невагомість – це стан тіла, у якому його вага дорівнює нулю. Для тіл на поверхні Землі або поруч із її поверхнею це свідчить про те, що на тіло діє лише сила тяжіння. У такому разі всі тіла рухаються з однаковим прискорення – прискоренням вільного падіння.

Відповідь: 1Г, 2Б, 3А, 4В.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів.

За першим законом термодинаміки $$ Q=\Delta U+A, $$ де \(Q\) – отримане системою тепло, \(\Delta U\) – зміна внутрішньої енергії, \(A\) – виконана системою робота.

1 Ізотермічний процес – процес змінювання стану газу деякої маси, що відбувається за незмінної температури. Тобто \(\Delta U=0\) і перший закон термодинаміки є вигляд $$ Q=A. $$ Тобто вся теплота, отримана тілом, витрачається на виконання ним роботи.

2 Адіабатний процес – це процес, який відбувається без теплообміну з навколишнім середовищем. Тобто \(Q=0\) і перший закон термодинаміки має вигляд: $$ \Delta U+A=0. $$ А отже $$ A=- \Delta U. $$ Цим виразом описано роботу, що відбувається за рахунок зміни внутрішньої енергії, а отже – охолодження.

3 Ізохорний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного об’єму. Робота в такому процесі не виконується, тому перший закон термодинаміки має вигляд $$ Q=\Delta U. $$ Отже, уся теплота, отримана тілом, витрачається на збільшення його внутрішньої енергії.

4 Ізобарний процес – процес змінювання стану даного газу деякої маси, що відбувається за незмінного тиску. Тоді перший закон термодинаміки має вигляд $$ Q=\Delta U+A. $$ Тож теплота, отримана тілом, витрачається на зміну внутрішньої енергії та роботу тіла.

Відповідь: 1Г, 2В, 3А, 4Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання розуміння природи струму в різних середовищах.

Характерні особливості проходження струму в різних середовищах такі:

A Електричний струм у газах (газовий розряд ) – це напрямлений рух вільних електронів, позитивних і негативних йонів.

У більшості газів у нормальному стані практично немає вільних носіїв заряду, що є ознакою діелектриків. Тому необхідно якось змусити електрони відділитися від атомів і приєднатися до інших, утворюючи і позитивні, і негативні йони. Цей процес, у результаті якого гази стають провідниками, називають йонізацією.

Щоб йонізувати газ, електронам у його атомах потрібно надати додаткової енергії, якої буде досить для того, щоби покинути атом. Є багато способів надати газу цю енергію, серед яких і термічна йонізація внаслідок нагрівання газу до високих температур. За термічної йонізації молекули рухаються настільки швидко, що часто стикаються одна з одною, у результаті таких зіткнень утворюються вільні електрони та йони.

Б Електричний струм у розчинах і розплавах електролітів – це напрямлений рух вільних йонів (як позитивних, так і негативних).

В Електричний струм у металах – це напрямлений рух вільних електронів.

Г Діелектрик – це речовина, яка погано проводить струм, а отже в ній майже немає зарядів що можуть вільно пересуватися.

Д У напівпровідниках \(n-\text{типу}\) електрична провідність зумовлена наявністю вільних електронів, а в провідниках \(p-\text{типу}\) – переміщенням порожніх місць, у яких електронів не вистачає, тобто дірок.

Відповідь: 1В, 2Б, 3А, 4Д.

ТЕМА: Коливання і хвилі. Поперечні та поздовжні хвилі. Довжина хвилі.

Завдання скеровано на оцінювання вміння розв’язувати задачі на основі аналізування графічного зображення хвиль.

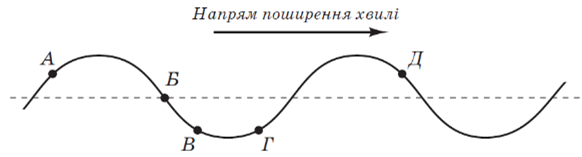
Рис. 1. Умова завдання

Поперечна хвиля – хвиля, у якій частинки середовища коливаються перпендикулярно до напрямку поширення хвилі. Хвиля, зображена в завданні, є поперечною.

У поперечній хвилі швидкість частинок у точках найбільшого відхилення від положення рівноваги дорівнює нулю.

Для точок перед найближчим гребнем (точки Б, В та Д) швидкість спрямована вгору, а для точок після гребня (точки А, Г) – униз (рис. 2). Точка перебуває перед найближчим гребнем, якщо гребінь рухається до неї.

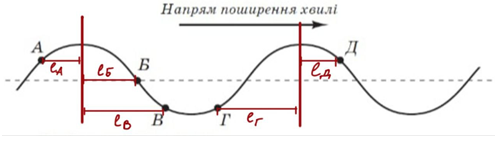
Рис. 2. Відстань від точок до гребенів хвиль

Якщо швидкість частинки зменшується, то її прискорення має протилежний напрямок до напрямку швидкості й навпаки. Прискорення частинок у поперечній хвилі завжди спрямоване до положення рівноваги, тож:

Точка А: швидкість спрямована вниз, прискорення – вниз.

Точка Б: швидкість спрямована вгору, прискорення дорівнює нулю.

Точка В: швидкість спрямована вгору, прискорення – вгору.

Точка Г: швидкість спрямована вниз, прискорення – вгору.

Точка Д: швидкість спрямована вгору, прискорення – вниз.

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Робота. Потужність. ККД.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з обчислення роботи, потужності й коефіцієнта корисної дії (ККД).

Дано:
\(h=10\ \text{м}\)
\(P=400\ \text{Вт}\)
\(t=5\ \text{хв}\)
\(V=600\ \text{л}\)
\(\mathbf{\rho}=1000\ \frac{\text{кг}}{\text{м}^3}\)

1. Знайти:
\(A\ (\text{кДж})\ -\ ?\)

Корисна робота – це робота, необхідна для виконання завдання. У цьому завданні це піднімання води об’ємом \(600\ \text{л}\) на висоту \(10\ \text{м}\). Роботу сили можна обчислити за формулою $$ A=Fs\cos\mathbf{\beta}, $$ де \(F\) – сила, що діє на тіло, \(s\) – переміщення тіла, \(\mathbf{\beta}\) – кут між напрямками векторів сили й переміщення.

Під час піднімання води насос працює проти сили тяжіння, тож найменша сила, яку можна прикласти для підйому води, дорівнює силі тяжіння, що діє на неї. Кут між напрямком дії сили, що піднімає воду, і переміщенням води дорівнює нулю. Тож \begin{gather*} A=F_\text{тяж}s;\\[7pt] F_\text{тяж}=mg;\\[7pt] A=mgh, \end{gather*} де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Маса води пов’язана з її об’ємом і густиною формулою \begin{gather*} m=\mathbf{\rho}V. \end{gather*}

Тоді

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД машини можна визначити за формулою $$ \text{ККД}=\frac{A_\text{кор}}{A_\text{пов}}\cdot 100\ \text{%}, $$ де \(A_\text{пов}\) – повна робота.

Повну роботу можна обчислити, якщо врахувати енергію, яку споживає електричний насос. Її можна визначити за такою формулою: \begin{gather*} A_\text{пов}=Pt, \end{gather*} де \(t\) – час роботи двигуна, \(P\) – потужність двигуна.

Тоді

Відповідь: 1. 60. 2. 50.

ТЕМА: Оптика. Електромагнітні хвилі. Кванти світла.

Завдання скеровано на перевірку розуміння зв’язку між характеристиками квантів світла й електромагнітних хвиль.

Дано:
\(\mathbf{\lambda}=0,55\ \text{мкм}\)
\(E_\text{min}=2,16\cdot 10^{-17}\ \text{Дж}\)
\(q=1,6\cdot 10^{-19}\ \text{Кл}\)
\(h=6,6\cdot 10^{-34}\ \text{Дж}\cdot\text{с}\)
\(c=3\cdot 10^8\ \text{м/с}\)

1. Знайти:
\(E\ (\text{еВ})\ -\ ?\)

Енергію фотона можна обчислити за формулою: $$ E=h\mathbf{\nu}, $$ де \(E\) – енергія фотона, \(\mathbf{\nu}\) – частота випромінювання, \(h\) – стала Планка.

Частота пов’язана з довжиною хвилі формулою \begin{gather*} \mathbf{\nu}=\frac{c}{\mathbf{\lambda}}, \end{gather*} де \(c\) – швидкість світла, \(\mathbf{\lambda}\) – довжина хвилі, \(\mathbf{\nu}\) – частота хвилі.

Тоді \begin{gather*} E=h\mathbf{\nu};\\[6pt] E=\frac{hc}{\mathbf{\lambda}};\\[6pt] E=6,6\cdot 10^{-34}\ \text{Дж}\cdot \ \text{с}\ \frac{3\cdot 10^8\ \text{м/с}}{0,55\ \text{мкм}};\\[6pt] E=6,6\cdot 10^{-34}\ \text{Дж}\cdot \ \text{с}\ \frac{3\cdot 10^8\ \text{м/с}}{0,55\cdot 10^{-6}\ \text{м}};\\[6pt] E=36\cdot 10^{-20}\ \text{Дж}. \end{gather*}

Отриманий результат можна перевести в еВ за формулою

2. Знайти:
\(N\ -\ ?\)

Для того, щоб око сприймало світло, на цій довжині хвилі сумарна енергія всіх фотонів, що потрапляють на сітківку, має дорівнювати мінімальній енергії: $$ E_\text{min}=NE. $$

Тоді кількість фотонів можна обчислити за формулою \begin{gather*} N=\frac{E_\text{min}}{E};\\[6pt] N=\frac{2,16\cdot 10^{-17}\ \text{Дж}}{36\cdot 10^{-20}\ \text{Дж}};\\[6pt] N=0,06\cdot 10^3;\\[7pt] N=60. \end{gather*}

Відповідь: 1. 2,25. 2. 60.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.

Дано:
\(m=250\ \text{кг}\)
\(a=0,2\ \text{м/с}^2\)

Знайти:
\(m\ (\text{кг})\ -\ ?\)

На аеростат діють дві сили: сила тяжіння і сила Архімеда. Сила Архімеда не залежить від маси баласту, а силу тяжіння можна визначити за формулою $$ F_\text{тяж}=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Тоді можна записати другий закон Ньютона для аеростата: $$ m\overrightarrow{a}=\overrightarrow{F_\text{тяж}}+\overrightarrow{F_\text{Арх}} $$

Сила тяжіння спрямована вниз, сила Архімеда – угору, до скидання балансу тіло аеростат опускається, тож прискорення також спрямоване вниз. Тоді векторне рівняння можна спроєктувати на вісь \(OY\): $$ -m_\text{до}a=-m_\text{до}g+F_\text{Арх}. $$

Після скидання баласту проєкція другого закону Ньютона матиме інший вигляд: $$ m_\text{після}a=-m_\text{після}g+F_\text{Арх}. $$

Тоді з рівняння для руху аеростата до скидання баласту можна виразити силу Архімеда: $$ F_\text{Арх}=m_\text{до}g-m_\text{до}a. $$

Тож:

Тоді маса скинутого баласту така:

Відповідь: 10.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про відносну вологість повітря.

Дано:
\(V=0,5\ \text{м}^3\)
\(\Delta m=6\ \text{г}\)
\(\mathbf{\rho}_\text{н.п.}=20\ \frac{\text{г}}{\text{м}^3}\)

Знайти:
\(\mathbf{\varphi}_\text{до}\ (\text{%})\ -\ ?\)

Маса води в повітрі перестає змінюватися, коли рідина й пара досягають стану динамічної рівноваги – кількість випаруваної рідини дорівнює кількості сконденсованої пари. Тобто маса води в повітрі перестає змінюватися, коли пара стає насиченою.

Масу води в повітрі, якщо пара є насиченою, обчислюють за формулою \begin{gather*} m_\text{після}=\mathbf{\rho}_\text{н.п.}V;\\[6pt] m_\text{після}=20\frac{\text{г}}{\text{м}^3}\cdot 0,5\ \text{м}^3;\\[6pt] m_\text{після}=10\ \text{г}. \end{gather*}

Тоді масу водяної пари в повітрі до випаровування обчислюють за формулою

Тож відносну вологість до випаровування обчислюють за формулою $$ \mathbf{\varphi}=\frac{\mathbf{\rho}_\text{а}}{\mathbf{\rho}_\text{н.п.}}\cdot 100\ \text{%}, $$ де \(\mathbf{\varphi}\) – відносна вологість повітря, \(\mathbf{\rho}_\text{н.п.}\) – густина насиченої пари, \(\mathbf{\rho}_\text{а}\) – густина водяної пари в повітрі. $$ \mathbf{\rho}_\text{а}=\frac{m_\text{до}}{V}=\frac{4\ \text{г}}{0,5\ \text{м}^3}=8\ \frac{\text{г}}{\text{м}^3}. $$

Тож

Відповідь: 40.

ТЕМА: Механіка. Основи динаміки. Сили. Тиск рідин та газів.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з використанням сили тиску.

Дано:
\(h=50\ \text{см}\)
\(S=40\ \text{см}^2\)
\(p=6\ 500\ \text{Па}\)

Знайти:
\(A\ (\text{Дж})\ -\ ?\)

Роботу можна визначити за формулою $$ A=Fh\cos\mathbf{\beta}, $$ де \(F\) – сила, що діє на тіло, \(h\) – переміщення тіла, \(\mathbf{\beta}\) – кут між напрямками векторів сили й переміщення.

На поршень діє сила тиску газу, яку можна визначити за формулою $$ F=pS, $$ де \(p\) – тиск, \(S\) – площа поверхні, на яку відбувається тиск.

Напрямок дії сили тиску завжди перпендикулярний до поверхні, що обмежує газ, тому кут між переміщенням поршня і напрямком дії сили тиску дорівнює нулю. Тож \begin{gather*} A=Fh;\\[7pt] A=pSh;\\[7pt] A=6\ 500\ \text{Па}\cdot 40\ \text{см}^2\cdot 50\ \text{см};\\[7pt] A=6\ 500\ \text{Па}\cdot 0,004\ \text{м}^2\cdot 0,5\ \text{м};\\[7pt] A=13\ \text{Дж}. \end{gather*}

Відповідь: 13.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку розуміння принципів паралельного і послідовного з’єднання конденсаторів.

Дано:
\(C_1=4\ \text{мкФ}\)
\(C_2=C_3=6\ \text{мкФ}\)
\(U=120\ \text{В}\)

Знайти:
\(E\ (\text{мДж})\ -\ ?\)

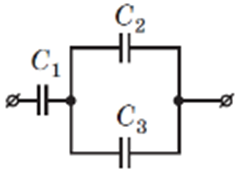
Рис. 1. Умова завдання

Енергію конденсатора можна визначити за формулою \begin{gather*} E=\frac{CU^2}{2}, \end{gather*} де \(U\) – напруга на обкладинках конденсатора, а \(C\) – його ємність.

Для визначення енергії системи конденсаторів необхідно визначити її сумарну ємність. Конденсатори 2 та 3 з’єднані паралельно, а до них послідовно підключений конденсатор 1.

Ємність батареї конденсаторів, з’єднаних паралельно, визначають за формулою \begin{gather*} C_{2-3}=C_2+C_3;\\[7pt] C_{2-3}=6\ \text{мкФ}+6\ \text{мкФ};\\[7pt] C_{2-3}=12\ \text{мкФ}. \end{gather*}

Ємність батареї конденсаторів, з’єднаних послідовно, визначають за формулою

Тоді енергію батареї конденсаторів обчислюємо за формулою

\begin{gather*} E=\frac{CU^2}{2};\\[6pt] E=\frac{3\ \text{мкФ}\cdot (120\ \text{В})^2}{2};\\[6pt] E=\frac{3\cdot 10^{-6}\cdot 14\ 400}{2};\\[6pt] E=0,0216\ \text{Дж};\\[7pt] E=21,6\ \text{мДж}. \end{gather*}

Відповідь: 21,6.

ТЕМА: Закони електролізу.

Завдання скеровано на перевірку вміння застосовувати закони електролізу для розв’язування розрахункових задач.

Дано:
\(m_0=80,25\ \text{г}\)
\(m=80,73\ \text{г}\)
\(I=1\ \text{А}\)
\(t=25\ \text{хв}\)

Знайти:
\(k\ \left(\frac{\text{мг}}{Кл}\right)\ -\ ?\)

В електролітичній ванні на катодній пластині збирається речовина, що виділилася внаслідок електролізу.

За першим законом електролізу можна визначити масу міді, що виділилася: $$ \Delta m=kIt, $$ де \(m\) – маса речовини, \(I\) – сила струму, \(t\) – час, \(k\) – електрохімічний еквівалент речовини.

Тоді можна визначити електрохімічний еквівалент:

Відповідь: 0,32.

ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії під час гармонічних коливань.

Завдання скеровано на оцінку вміння розв’язувати комбіновані задачі, які передбачають обробку й аналіз результатів експерименту, зображених на рисунку, i використання законів збереження енергії в коливальному процесі.

Знайти:
\(V_\text{max}\ \left(\frac{\text{см}}{\text{с}}\right)\ -\ ?\)

З рисункa 1 можна визначити довжину гумки у двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, а отже його швидкість \(V\) дорівнює нулю.

\begin{gather*} x_\text{мін}=16\ \text{см};\\[7pt] x_\text{макс}=20\ \text{см}. \end{gather*}

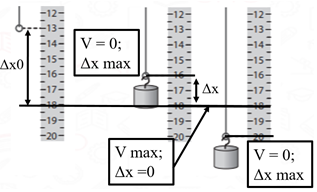
Рис. 1. Крайні положення тягарця

За цими значеннями можна обчислити амплітуду коливань:

Знаючи амплітуду коливань, можна визначити положення рівноваги – таке положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю припиняться:

Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.

Під час коливань зберігається повна механічна енергія системи \(W\): $$ W=W_k+W_n=const, $$ де \(W_k\) – кінетична енергія, \(W_n\) – потенціальна енергія.

Кінетичну енергію можна визначити за формулою $$ W_k=\frac{mV^2}{2}, $$ де \(m\) – маса тіла.

Оскільки для гумової стрічки виконуваний закон Гука, можна обчислити потенціальну енергію за формулою, якою описують потенціальну енергію розтягнутої пружини: $$ W_n=\frac{k\Delta x^2}{2}, $$ де \(k\) – коефіцієнт жорсткості пружини, а \(\Delta x\) – розтяг пружини (гумової стрічки).

Хоча повна механічна енергія системи зберігається, але значення кінетичної і потенціальної енергії постійно змінюється під час коливань.

У крайніх положеннях швидкість тягарця дорівнює нулю, а отже і його кінетична енергія теж. А от відхилення від положення рівноваги в цих положеннях найбільше, тому потенціальна енергія максимальна.

У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, отже кінетична енергія приймає найбільше значення, а потенціальна перетворюється на нуль.

Зважаючи на закон збереження енергії і спостереження, описані вище, можна записати таку рівність:

Тоді можна виразити максимальну швидкість: $$ V_{max}=\sqrt{\frac{k\Delta x_{max}^2}{m}}=\sqrt{\frac km}\Delta x_{max}. $$

Відношення \(\frac km\) невідоме, але його можна визначити.

У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати другий закон Ньютона: $$ mg=F_\text{пр}, $$ де \(F_\text{пр}\) – це сила пружності, що діє на тягарець з боку гумової стрічки. Її можна визначити за формулою $$ F_\text{пр}=k\Delta x_0, $$ де \(\Delta x_0\) – розтяг пружини під вагою тягарця:

\begin{gather*} \Delta x_0=x_\text{рівн}-x_0;\\[7pt] \Delta x_0=18\ \text{см}-13\ \text{см};\\[7pt] \Delta x_0=5\ \text{см}, \end{gather*} де \(x_0\) – це довжина пружини без тягарця.

Тоді \begin{gather*} mg=k\Delta x_0;\\[6pt] \frac km=\frac{g}{\Delta x_0}. \end{gather*}

Після цього можна підставити отримане відношення у вираз для максимальної швидкості:

Відповідь: 28.

ТЕМА: Електродинаміка. Закони постійного струму. Електрорушійна сила.

Завдання скеровано на перевірку вміння аналізувати графіки тригонометричних залежностей фізичних величин.

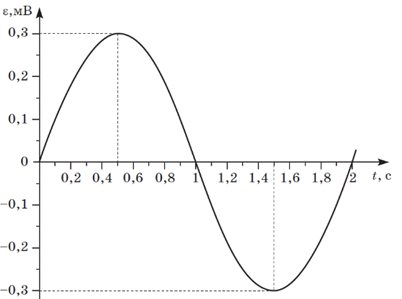
Рис. 1. Умова завдання

Знайти:
\(\text{ЕРС}\ (\text{мВ})\ -\ ?\)

Графік, зображений на рисунку 1, – це графік синусоїдальної залежності, тож електрорушійна сила (ЕРС) залежить від часу: $$ \mathbf{\varepsilon}=A\sin\mathbf{\omega}t, $$ де \(A\) – амплітуда коливань, \(\mathbf{\omega}\) – циклічна частота коливань, \(t\) – момент часу.

Циклічна частота пов’язана з періодом формулою $$ \mathbf{\omega}=\frac{2\mathbf{\pi}}{T}. $$

За графіком можна також визначити амплітуду коливань, яка дорівнює максимальному відхиленню від положення рівноваги: $$ A=0,3\ \text{мВ}, $$ тож $$ \mathbf{\varepsilon}=0,3\sin\frac{2\mathbf{\pi}}{T}t. $$

Тоді можна обчислити ЕРС в момент часу \(t=\frac{T}{12}\):

Відповідь: 0,15.

ТЕМА: Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням релятивістського закону додавання швидкостей.

Дано:
\(v_\text{рух}=0,5\ \text{с}\)
\(v_\text{кат}=0,5\ \text{с}\)

Знайти:
\(\frac{c}{v_\text{нерух}}\ -\ ?\)

Усі тіла рухаються зі швидкістю, порівнюваною зі швидкістю світла. Тому в цьому разі для додавання швидкостей необхідно використовувати релятивістський закон: $$ v_\text{нерух}=\frac{v_\text{рух}+v_\text{кат}}{1+\frac{v_\text{рух}v_\text{кат}}{c^2}} $$ де \(v\) – швидкість руху тіла відносно нерухомої системи відліку (Землі), \(v_\text{кат}\) – швидкість руху тіла відносно рухомої системи відліку (ракети), \(v_\text{рух}\) – швидкість рухомої системи відліку (ракети).

Тож

\begin{gather*} \frac{c}{v_\text{нерух}}=c:\frac{v_\text{рух}+v_\text{кат}}{1+\frac{v_\text{рух}v_\text{кат}}{c^2}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{v_\text{рух}v_\text{кат}}{c^2}}{v_\text{рух}+v_\text{кат}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{0,5\ \text{с}\cdot 0,5\ \text{с}}{c^2}}{0,5\ \text{с}+0,5\ \text{с}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{0,25\ \text{с}^2}{c^2}}{c};\\[6pt] \frac{c}{v_\text{нерух}}=1,25. \end{gather*}

Відповідь: 1,25.