ЗНО онлайн 2017 року з фізики – додаткова сесія
Тестові завдання додаткової сесії ЗНО 2017 року з фізики
ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку розуміння поняття «переміщення».
Переміщення – це векторна величина, яку графічно зображують як напрямлений відрізок прямої, що з’єднує початкове і кінцеве положення матеріальної точки.
Земля за рік робить повний оберт навколо Сонця – проходить повне коло. Відповідно за пів року Земля пройде половину кола (рис. 1).
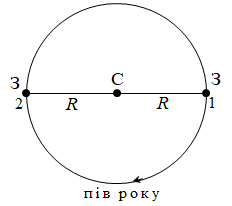
Рис. 1. Рух Землі навколо Сонця: 1 – початкове положення Землі; 2 ‑ кінцеве положення Землі (через пів року);
Якщо з’єднати початкове положення Землі (точка 1) із кінцевим (точка 2), де вона опиниться через пів року, то відрізок 1–2 буде діаметром орбіти, якою рухається планета. Оскільки радіус орбіти за умовою дорівнює
Інші варіанти відповіді можна отримати, якщо сплутати переміщення зі шляхом й обчислювати не довжину відрізка, яким з’єднані початкове і кінцеве положення тіла, а визначати довжину траєкторії руху тіла. Також до неправильної відповіді може призвести нерозуміння закономірностей руху Землі навколо Сонця.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.
Завдання скеровано на перевірку вміння застосовувати закон додавання швидкостей.
Закон додавання швидкостей полягає в тому, що швидкість
Якщо відома швидкість руху другої мурахи відносно землі
Спочатку потрібно вибрати напрямок (зліва направо) горизонтальної oсі Ох, уздовж якої рухаються всі мурахи:

Якщо перша мураха біжить у напрямку осі, то модуль її швидкості дорівнює
Швидкість руху другої мурахи відносно землі дорівнює
Третя мураха рухається в тому самому напрямку, що й перша, зі швидкістю
Тож можна обчислити швидкість руху другої мурахи відносно третьої:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Сили пружності. Закон Гука.
Завдання скеровано на перевірку розуміння залежності сили пружності від видовження тіла під час малих пружних деформацій.
За законом Гука в разі малих пружних деформацій розтягнення або стиснення сила пружності
Між силою пружності й видовженням залежність лінійна, тож графіком функції є пряма. На графіку, наведеному в умові завдання, прямолінійною є лише ділянка
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Кінетична та потенціальна енергія.
Завдання скеровано на розуміння чинників, від яких залежить величина кінетичної енергії тіла.
Кінетична енергія – це фізична величина, якою характеризують механічний стан рухомого тіла. Кінетичну енергію
За умовою завдання маса тіл однакова, тому кінетична енергія змінюватиметься прямо пропорційно швидкості руху тіла. Із наведених у варіантах відповіді рівнянь залежності координати тіла від часу можна визначити швидкості руху кожного із чотирьох тіл. Цими рівняннями описано прямолінійний рівномірний рух тіл:
Тобто множник
Найбільша швидкість руху з-поміж наведених –
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Прості механізми.
Завдання скеровано на перевірку розуміння принципу дії простих механізмів – важеля і рухомого блока.
Прості механізми − це пристрої, які дають змогу виконувати роботу, докладаючи меншу силу порівняно з виконанням цієї ж роботи без них (виграємо в силі – програємо у відстані), або ж змінювати напрямок дії сили на зручніший для людини.
Важіль перебуває в рівновазі, якщо моменти сил, що обертають його за годинниковою стрілкою і проти неї, за модулем дорівнюють один одному.
Проти годинникової стрілки важіль обертатиме сила тяжіння, що діє на вантаж 1. Плече цієї сили становитиме
За годинниковою стрілкою важіль обертатиме сила, що натягує підвіс, на якому підвішено рухомий блок. Використання рухомого блока забезпечує подвійний виграш у силі. Тож для тримання вантажу 2 треба прикласти вдвічі меншу силу порівняно з його вагою. Плече цієї сили дорівнює
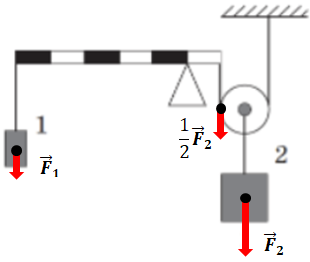
Запис правила моментів сил як умови рівноваги для тіла, що лише обертається, тобто має нерухому вісь обертання, такий:
Відповідно
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.
Завдання скеровано на перевірку розуміння процесів, що відбуваються з газом сталої маси, тобто ізопроцесів.
За першим законом термодинаміки передана системі кількість теплоти
Під час ізотермічного
Під час ізобарного
Під час адіабатного (без обміну теплом із навколишнім середовищем) процесу теплота системі не передається, тобто газ може виконати роботу за рахунок зменшення внутрішньої енергії, при цьому температура газу зменшиться:
За ізохорного
Тож саме під час ізохорного процесу всю передану газу кількість теплоти буде витрачено на зміну його внутрішньої енергії.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Змочування.
Завдання скеровано на розуміння того, як поводить себе змочувальна або не змочувальна рідина в капілярах.
В умові завдання зазначено, що капіляр (тонка трубочка з дуже вузьким внутрішнім каналом) чистий ізсередини і ззовні. Це означає, що жодна стороння речовина не заважатиме взаємодії рідини зі склом (змочуватиме скло чи ні).
Що тонший капіляр, то вище підніматиметься в ньому рідина. Рівень рідини в капілярі не може бути нижчим від загального рівня рідини в посудині, у яку капіляр уставлено.
Якщо рідина змочує стінки капіляра, то біля його стінок вона набуватиме ввігнутої форми і ззовні і зсередини, оскільки зазначено, що капіляр чистий з обох боків.
Якщо ж рідина не змочує скло, то її поверхня біля стінок капіляра буде опуклою і ззовні, і зсередини.
Отже, єдиний правильний рисунок із-поміж наведених – рисунок B: рідина в капілярі піднялася вище від загального рівня, а вода і ззовні, і зсередини змочує скло.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.
Завдання скеровано на перевірку розуміння умов виконання роботи в термодинаміці, залежності її від деяких фізичних величин, а також вміння тлумачити графіки й брати з них числові дані для розв’язування задачі.
З формули для визначення роботи
зрозуміло: якщо об’єм газу не зазнає змін, то робота не буде виконана, тобто дорівнюватиме нулю.
На графіку ділянка 12 відповідає ізохорному охолодженню (знижуються температура й тиск, відповідно третій макроскопічний параметр газу – об᾽єм – залишатиметься сталим), ділянка 23 – ізобарному нагріванню (тиск залишається сталим, температура підвищується, відповідно об’єм збільшуватиметься).
Цих висновків можна дійти з огляду на рівняння Клапейрона:
Якщо під час процесу 12 об’єм не змінюється, то газ не виконує роботу, робота газу на цій ділянці дорівнює нулю. Тоді робота газу під час переходу зі стану 1 у стан 3 складатиметься лише з роботи на ділянці 23.
Об᾽єм унаслідок ізобарного нагрівання зміниться так:
Звідси
Відповідно робота
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.
Завдання скеровано на розуміння закону збереження електричного заряду.
За законом збереження електричного заряду в замкненій системі тіл повний заряд залишається незмінним, заряд не може звідкись виникнути або кудись зникнути, заряди лише перерозподіляються між тілами системи, що контактують між собою.
Оскільки заряд накопичується на поверхні провідників, то не має значення, що одна з куль порожниста, як зазначено в умові. Головне, що зовнішні параметри в них однакові. У куль однакового радіуса площа зовнішньої поверхні та сама. Кулі виготовленого з одного матеріалу. Тому після дотику заряд перерозподілиться порівну між кулями, і заряд кульки 1 дорівнюватиме заряду кульки 2.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Принцип суперпозиції полів.
Завдання скеровано на перевірку вміння геометрично інтерпретувати дію кількох електричних полів у точці простору.
Електричне поле можна зобразити графічно лініями напруженості.
Якщо в точці простору електричне поле створене системою зарядів, то напруженість цього результувального поля дорівнюватиме векторній сумі напруженостей полів цих зарядів.
За напрямок напруженості в точці електричного поля потрібно взяти напрямок сили, яка діяла б на пробний позитивний заряд, якби він був поміщений у цю точку поля.
На рисунку в умові завдання зображено два негативні заряди. Під час взаємодії з умовним позитивним зарядом в точці
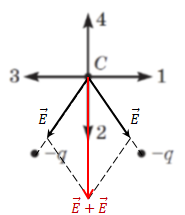
Якщо добудувати на цих векторах напруженості паралелограм, то за правилом додавання векторів можна визначити їхню векторну суму – більшу діагональ побудованого паралелограма. Вона збігатиметься з напрямком 2.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Електровимірювальні прилади.
Завдання скеровано на перевірку розуміння деяких правил складання електричних кіл і підключення до них різних приладів.
Ні амперметр, ні вольтметр не мають впливати на значення вимірюваної величини, як будь-який вимірювальний прилад. До того ж в умові зазначено, що прилади та провідники є ідеальними. Це означає, що опором провідників можна знехтувати, а опір ідеального амперметра вважати рівним нулю. За цих умов послідовно підключений в електричне коло амперметр без утрат покаже значення тієї сили струму, що проходить через споживач (тут – резистор).
На відміну від амперметра опір ідеального вольтметра нескінченно великий. Такий опір не дає змоги струму проходити через вольтметр. Тому вольтметр показує точне значення напруги на ділянці кола, до якої він приєднаний паралельно. Тож підключення в електричному колі амперметра паралельно, а вольтметра послідовно зі споживачем є неправильним.
Якщо підключити вольтметр паралельно до споживача або до ділянки кола, де послідовно з’єднано амперметр і споживач, то вольтметр покаже падіння напруги на споживачі (амперметр ідеальний, тому не впливатиме на значення напруги).
Якщо підключити вольтметр паралельно лише до амперметра, за законом Ома для ділянки кола напруга на амперметрі дорівнюватиме нулю, оскільки опір амперметра вважаємо рівним нулю:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах.
Завдання скеровано на перевірку розуміння протікання електричного струму в різних середовищах, залежності сили струму від температури.
В розчинах або розплавах електролітів носіями електричного заряду є вільні йони. Із підвищенням температури кількість таких йонів значно збільшується. Тому, попри збільшення кількості зіткнень йонів, опір розчину або розплаву електроліту зменшується, а сила струму за незмінної напруги, відповідно, збільшується.
У газах за підвищення температури збільшується концентрація носіїв заряду – вільних електронів, позитивних і негативних йонів. Це приводить до зменшення опору й, відповідно, збільшенню сили струму.
Провідність напівпровідників зумовлена або вільними електронами, або переміщенням дірок. Із підвищенням температури зростає енергія теплового руху електронів і, як наслідок, збільшується кількість пар «електрон – дірка» в напівпровіднику. Збільшення кількості носіїв заряду приводить до збільшення провідності та зменшення опору. Відповідно зменшення опору веде до зростання сили струму.
У металах позитивні йони коливаються навколо положення рівноваги, а відносно вільні електрони переносять заряд. Середня швидкість теплового руху електронів провідності й енергія коливань йонів у вузлах кристалічних ґраток збільшуються з підвищенням температури металевого провідника. Унаслідок цього зростає і частота зіткнень електронів із йонами, що приводить до збільшення опору провідника та зменшення сили струму.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Змінний електричний струм.
Завдання скеровано на перевірку розуміння умов виникнення змінного електричного струму й законів, якими описують його.
У рамці, яка зі сталою кутовою швидкістю обертається в магнітному полі, індукуватиметься змінна електрорушійна сила (ЕРС), яка змінюватиметься за гармонічним законом – із часом за законом синуса або косинуса.
Кут
Тому й магнітний потік
Відповідно ЕРС індукції
Згідно із законом Ома миттєве значення сили струму
Отже, сила струму пропорційна часу, але під тригонометричною функцією. Тому із часом сила струму так само, як ЕРС індукції, змінюватиметься за законом синуса (або косинуса за певних умов).
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку розуміння особливостей коливання на пружині, фізичних величин, якими ці коливання описують, і закономірностей переходу одного виду енергії в інший.
Причиною коливань за умовою є сила пружності, що виникла в деформованій пружині. Оскільки ця пружина спільна для обох тягарців, то однаковою для них буде саме частота коливань пружини (пружина буде одночасно скорочуватися і видовжуватися для обох тіл, а частота – це кількість коливань за певний проміжок часу).
Потенціальна енергія пружини переходитиме в кінетичну енергію тягарця і навпаки. За умовою механічна енергія зберігається (утрати на тертя не враховуємо). Кінетична енергія прямо пропорційна масі, а маси тягарців різняться у 2 рази. Тому максимальна швидкість і, відповідно, максимальна кінетична енергія також різні. Оскільки потенціальна енергія теж різна, то й максимальне видовження пружини ‒ амплітуда ‒ різнитиметься для різних за масою тягарців.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Вільні механічні коливання.
Завдання скеровано на розпізнання вільних механічних коливань у реальних прикладах.
Вільними є коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги. Тобто певна зовнішня сила один раз подіяла на систему й після цього система сама виконує коливання.
На голку діє періодична зовнішня сила від обертання ручним чи ножним механічним або електроприводом. Ця сила, передана через усі необхідні для цього складники швейної машинки, змушує голку підніматися й опускатися.
Коливання буйка під дією хвиль і штори під дією протягу підтримуються нехай не періодичною зовнішньою силою, але силою, що діє постійно.
Пташка, коли злітала з гілочки, один раз відштовхнулася від неї, а після цього гілочка сама продовжила коливання, тому саме ці коливання є вільними.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.
Коливання в коливальному контурі відбуваються за гармонічним законом:
У даному випадку за гармонічним законом змінюється напруга
За активного опору
Однак у будь-якій реальній коливальній системі завжди є втрати енергії: під час механічних коливань енергія витрачається на долання сил тертя, деформацію; під час електромагнітних коливань – на нагрівання провідників, випромінювання електромагнітних хвиль тощо. Унаслідок цього амплітуда коливань із часом зменшується. А через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються (згасають). Тому вільні коливання завжди є згасними.
В умові не задано амплітудне значення напруги. Тому обчислимо циклічну частоту
Отже, рівняння, що відповідає умові завдання,
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Повне відбивання.
Завдання скеровано на перевірку розуміння явища повного відбивання і вміння бачити (виявляти) це явище в реальних прикладах.
Повне відбивання світла спостерігають, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини.
Світловод – це волокно зі скла чи штучного матеріалу, а також трубка або плівка для передавання світла навіть на дуже великі відстані завдяки ефекту багаторазового повного внутрішнього відбивання. Світловоди використовують у телетрансляції, у медичних приладах для спостереження органів ізсередини (ендоскопія) тощо.
Коли світло поширюється в тумані, то воно розсіюється – багато разів невпорядковано змінює напрямок, відбиваючись від великої кількості маленьких крапельок води.
Якщо розмір отвору, крізь який проходить світло, такого ж порядку, як довжина світлової хвилі, то спостерігають дифракцію – огинання країв вузького отвору та проникнення світла в ділянку геометричної тіні. Наприклад, під час світіння ліхтаря промені відбиваються від його обмежувальної поверхні й на краях напрямленого пучка світла можна побачити дифракцію.
Отже, повне відбивання спостерігають під час поширення світла у світловоді.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.
Завдання скеровано на перевірку розуміння потужності й уміння визначати її.
Потужність випромінювання
Виділення тілом енергії (випромінювання) супроводжується зменшенням його маси. Зміна енергії тіла прямо пропорційна зміні його маси:
Відповідно
Перед обчисленням потрібно перевести значення часу в систему СІ:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Випромінювання і поглинання світла атомом. Оптика.
Завдання скеровано на перевірку розуміння природи світла.
Природу світла пояснюють двома різними теоріями – корпускулярною і хвильовою.
Згідно з корпускулярною теорією світло – це потік корпускул (частинок), випромінюваних світними тілами, а рух світлових корпускул підпорядкований законам механіки.
За хвильовою теорією світло – це поздовжні механічні хвилі, що поширюються у світовому ефірі – гіпотетичному пружному середовищі, яке заповнює весь світовий простір.
Отже, першою теорією можна пояснити деякі властивості світла, а ті властивості, які нею пояснити неможливо, пояснюють другою теорією.
Розкладання світла у спектр – дисперсію світла – пояснюють залежністю абсолютного показника заломлення середовища від частоти світлової хвилі, а не корпускулярною природою.
Інтерференція – накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.
Фотоефектом називають взаємодію світла з речовиною, супроводжувану випромінюванням (емісією) електронів (частинок). Тому все, що стосується фотоефекту, пояснюють корпускулярною теорією.
Відповідно до теорії Бора атоми випромінюють світло квантами. Це правильне твердження. Квант ‒ це елементарна дискретна неподільна частка, порція світлової енергії. Для опису їхніх корпускулярних властивостей використовують закони не класичної, а квантової механіки.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрування йонізувального випромінювання.
Завдання скеровано на перевірку знання і розуміння дії пристроїв для реєстрування йонізувального випромінювання.
Загальний принцип реєстрування йонізувального випромінювання полягає в реєстрації дії цього випромінювання.
Бульбашкова камера є трековим детектором. Робочим тілом у бульбашковій камері є перегріта рідина: йони, які утворюються вздовж траєкторії руху частинки, стають центрами кипіння. Унаслідок цього виникає ланцюжок бульбашок, за якими й фіксують випромінювану частинку (випромінювання)
Унаслідок руху швидкої зарядженої частинки в шарі фотоемульсії проступають сліди (треки) первинної частинки та всіх заряджених частинок, що виникли внаслідок ядерних взаємодій. За товщиною і довжиною треків можна визначити заряди частинок та їхню енергію.
Газорозрядний лічильник і йонізаційна камера працюють за одним принципом: робоче тіло – газ – розміщено в електричному полі з високою напругою; заряджена частинка, що пролітає крізь газ, йонізує його, і в пристрої виникає газовий розряд.
Камера Вільсона – також трековий детектор. Це контейнер, заповнений парою спирту або ефіру. Під час різкого опускання поршню пара внаслідок адіабатного розширення охолоджується і стає перенасиченою. Заряджена частинка, потрапивши в перенасичену пару, йонізує на своєму шляху молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари вздовж траєкторії руху (треку) частинки знімають на камеру або фотографують.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Молекулярна фізика і термодинаміка. Електродинаміка.
Завдання скеровано на перевірку знань і розуміння принципів дії пристроїв і механізмів із різних розділів фізики.
Гальмівні механізми (дискові або барабанні) не дають обертатися колесам, унаслідок чого автомобіль зменшує швидкість. Принцип дії гальмівного механізму заснований на використанні сили тертя. Під час гальмування кінетична енергія переходить у внутрішню.
Тепловий двигун – це машина, яка працює циклічно й перетворює енергію палива на механічну роботу. Робоче тіло (газ, який виконує роботу під час свого розширення) отримує певну кількість теплоти від нагрівника. Ця теплота частково перетворюється на механічну енергію (робоче тіло виконує роботу), а частково передається холодильнику.
Індукційні генератори струму перетворюють механічну енергію на електричний струм. Складені з металевого осердя, у пази якого поміщено обмотку. Кінці обмотки з’єднані з кільцями, до кожного з яких притиснуто щітку для відведення напруги до споживача. Осердя з обмоткою (ротор) обертається в магнітному полі нерухомого постійного магніту або електромагніту.
Електричний двигун є пристроєм для перетворення електричної енергії на механічну та приведення до руху машин і механізмів. Робота електродвигуна основана на втягуванні або виштовхуванні провідника з електричним струмом у магнітному полі й дії на провідник зі струмом сили Ампера. Під час роботи двигуна рух ротора (рухомої частини двигуна) передається валу, а з нього – безпосередньо до споживача.
Відповідь: 1А, 2Б, 3В, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та експериментальне обґрунтування їх.
Завдання скеровано на перевірку розуміння будови речовини в різних фазових (агрегатних) станах.
Кристал солі – це тверда йонна речовина. У ній йони розташовані в певному порядку (утворюють кристалічні ґратки) на відстанях, порівнюваних із розмірами йонів. Тому електростатичні сили втримують йони, що здійснюють малі коливання навколо положень рівноваги.
Вода в басейні – рідина. Молекули рідини розташовані хаотично. Середня відстань між молекулами порівняна з їхніми розмірами. Тому міжмолекулярні сили втримують молекули біля положення рівноваги. Кожна молекула рідини певний час (бл. 10–11 с) здійснює рух, подібний до коливального, потім перескакує в інше місце та знову коливається біля нового положення рівноваги. Час «осідлого життя» молекули в сотні разів більший за час «переходу».
Атмосферний кисень – газ. Молекули газів розташовані безладно й на відстанях, які в десятки разів більші за розміри самих молекул. На таких відстанях молекули майже не взаємодіють одна з одною. Тому, безперервно зіштовхуючись, молекули газів розлітаються на всі боки доти, доки не зустрінуть якусь перешкоду, наприклад, стінки посудини.
Йонізований газ – це плазма, так званий четвертий агрегатний стан речовини. Слово «йонізований» означає, що від значної частини атомів або молекул відокремлений принаймні один електрон. Плазма має властивості, схожі на газоподібний стан речовини (частинки рухаються вільно й відстань між частинками значно більша за розмір частинок). На відміну від газу в плазмі є далекосяжна кулонівська взаємодія між частинками, тобто вони взаємодіють навіть на великих відстанях.
Відповідь: 1В, 2Б, 3А, 4Д.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.
Завдання скеровано на перевірку розуміння дії магнітного поля на провідник з електричним струмом.
Силу, із якою магнітне поле діє на провідник зі струмом, називають силою Ампера
Напрямок дії сили Ампера визначають за правилом лівої руки: якщо ліву руку розташувати так, щоб лінії магнітної індукції
Розгляньмо кожний зображений варіант. Ліву руку орієнтуватимемо відносно сторінки з рисунком.
На рисунку 1 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка від вас (позначено хрестиком). Отже, орієнтуємо ліву руку долонею до себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
На рисунку 2 вектор магнітної індукції напрямлений вертикально вниз, отже долоню орієнтуємо торцем (перпендикулярно) до площини рисунка, а чотири пальці руки спрямовуємо праворуч за напрямком сили струму. Тоді великий палець, відігнутий на
На рисунку 3 сила Ампера не діятиме, оскільки напрямок сили струму збігається з напрямком вектора магнітної індукції і неможливо зорієнтувати ліву руку відповідно до правила визначення сили Ампера. За формулою сила Ампера також дорівнює нулю. Оскільки кут
На рисунку 4 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка до вас (позначено точками). Отже, орієнтуємо ліву руку долонею від себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
Відповідь: 1А, 2В, 3Д, 4Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних хвиль. Властивості електромагнітного випромінювання різних діапазонів.
Завдання скеровано на перевірку знань про різні види електромагнітного випромінювання і їхні джерела.
Під час розпаду радіонуклідів у ядерному реакторі виникає радіоактивне випромінювання, один із видів якого – гамма-промені.
Будь-які тіла, температура яких вища від абсолютного нуля, випромінюють інфрачервоні промені. Саме на цьому ґрунтується застосування їх у тепловізорах – приладах нічного бачення. Тому гарячий чай є джерелом інфрачервоного (теплового) випромінювання.
Радіохвилі – від наддовгих із довжиною понад
Люмінофор – речовина, яка здатна світитися за збудження, тобто люмінесціювати. Люмінофори широко використовують в електроніці, наприклад, ними вкривають екран телевізора, електропроменевої трубки, де їхнє світіння за бомбардування електронами формує зображення, у сцинтиляційних лічильниках тощо. Людське око сприймає це світіння, отже це діапазон видимого світла.
Відповідь: 1В, 2А, 3Г, 4Д.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.
Завдання скеровано на перевірку вміння визначати основні кінематичні характеристики, якими описують рівноприскорений рух, а саме проєкцію швидкості й прискорення.
1. За умовою рух є рівноприскореним, підтвердженням цього також є наведений графік залежності координати від часу. Графіком є частина параболи, вершина якої відповідає точці розвороту. Це саме момент часу
Відповідь: 0.
2. Рівняння координати для прямолінійного рівноприскореного руху в загальному вигляді таке:
Розгляньмо проміжок часу від
Спростімо рівняння:
Виразімо й обчислімо прискорення руху тіла:
Знак «мінус» вказує на те, що тіло рухається у протилежному до осі
Відповідь: –1.
Відповідь: 1. 0. 2. –1.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Коефіцієнт корисної дії.
Завдання скеровано на перевірку розуміння процесу згоряння палива й уміння обчислити коефіцієнт корисної дії.
1. Піч виконала корисну роботу – вода закипіла. Запишімо формулу для визначення кількості теплоти, яку отримала вода для того, щоб закипіти. Оскільки початкова температура води за умовою була
Значення об’єму переведімо в одиниці системи СІ:
Відповідь: 3,78.
2. Запишімо формулу для визначення коефіцієнта корисної дії
Корисно спожиту водою кількість теплоти
Обчислімо значення кількості теплоти, що виділилася:
Обчислімо коефіцієнт корисної дії печі:
Можна зробити висновок, що коефіцієнт корисної дії печі дуже низький, багато втрат – нагрівається сама піч, навколишнє повітря і предмети.
Відповідь: 10.
Відповідь: 1. 3,78. 2. 10.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умови плавання тіл.
Завдання скеровано на перевірку розуміння умов плавання тіл і вміння математично описати їх.
У завданні тричі змінюються умови плавання дерев’яного бруска. Опишімо кожен із випадків.
1. На брусок діє сила тяжіння, яку врівноважує сила Архімеда:
2. Коли до бруска знизу прикріпили вантаж, то виштовхувальна сила діятиме і на занурену частину бруска, і на вантаж. Запишімо умову плавання бруска за цих умов:
3. Розгляньмо третій випадок, коли вантаж поклали на брусок зверху. Запишімо умову плавання:
Розв’яжімо систему трьох рівнянь:
Віднімімо від рівняння (2) рівняння (3):
Підставімо в рівняння (3) вираз замість
Розкриймо дужки й обчислімо
Відповідь: 15.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин і газів. Тиск. Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.
Завдання скеровано на перевірку вміння розв’язувати розрахункові комбіновані задачі з визначення сили тиску (механіка), описавши стан газу рівнянням Клапейрона (молекулярна фізика).
Опишімо стан газу в циліндрі за початкових умов (див. рис. 1). Легкий поршень ділить циліндр на дві рівні частини. Позначмо тиск, що однаково діє на поршень з обох боків
Коли з певною силою поршень змістили, то стан газу в обох частинах циліндра змінився. Запишімо рівняння Клапейрона для обох частин циліндра:
Із цих рівностей визначмо тиски
Щоб утримувати поршень у положенні як на рисунку 2, треба прикласти до поршня силу, щоб компенсувати різницю цих тисків:
Обчислімо шукану силу за формулою:
Відповідь: 1,6.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Питома теплоємність речовини.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про фазові переходи.
Розгляньмо наведений в умові графік. Ділянка, на якій протягом двох хвилин (від 1‑ої до 3‑ої) температура речовини не змінювалася, відповідає плавленню, під час якого вся кількість теплоти
Потужність
Тепер розгляньмо ділянку графіка від 3‑ої до 4‑ої хвилини. Речовина розплавилася і почала нагріватися. Під час цього вона отримає кількість теплоти
Прирівняймо ці два вирази для потужності:
Масу можна скоротити й дістати вираз шуканої величини ‒ питомої теплоємності:
Відповідь: 2,5.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння розв’язувати задачі із застосування закону Ома для ділянки кола за різних з’єднань провідників.
Загальна напруга
За паралельного з’єднання провідників сила струму
Загальний опір
За законом Ома для ділянки кола
Звідси формула для обчислення
Отже, максимально можлива кількість резисторів у цьому колі може бути
Відповідь: 15.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Закони електролізу. Закони постійного струму. Закон Джоуля – Ленца.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі з тем різних розділів, а саме застосування закону Джоуля – Ленца під час електролізу.
Кількість теплоти
За умовою опір розчину електроліту й час електролізу відомі. Силу струму можна визначити з першого закону Фарадея:
Підставмо значення всіх величин й обчислімо кількість теплоти, що виділиться під час електролізу:
Відповідь: 90.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на перевірку вміння розв’язувати задачі про поширення механічних хвиль.
На рисунку позначмо період.
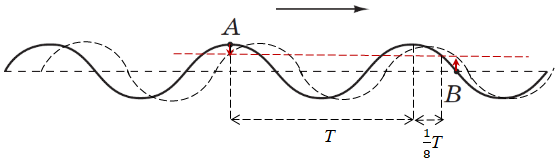
Через шуканий час
Відповідь: 0,2.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.
Завдання скеровано на перевірку вміння застосовувати закони відбивання світла для розв’язування задач із геометричної оптики.
За законом відбивання світла падний промінь, відбитий промінь і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині. А також кут відбивання
Зобразімо це на рисунку.
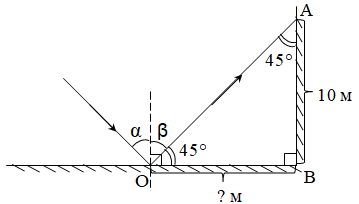
За умовою кут
Найкоротшою відстанню від точки падіння променя на калюжу до стіни школи є перпендикуляр, проведений від цієї точки до стіни школи. Тоді
Відповідь: 10.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння поняття «доза опромінювання людини» й методів визначення її.
Фізичну величину, якою характеризують біологічний вплив поглинутої дози йонізувального випромінювання, називають еквівалентною дозою йонізувального випромінювання
Обчислімо поглинуту за добу дозу:
Урахуємо також дозу опромінювання від рентгенівського медичного обстеження організму –
А це означає, що без шкоди для здоров᾽я людина може проходити рентгенівські медичні обстеження організму лише раз на рік, оскільки за умовою річна допустима доза опромінювання становить
Відповідь: 1.
Знайшли помилку? Пишіть на




