ЗНО онлайн 2018 року з фізики – пробний тест
Тестові завдання пробного тесту ЗНО 2018 року з фізики
ТЕМА: Механіка. Кінематика. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку розуміння поняття переміщення.
Переміщення
Літак, який рухається вздовж меридіану від полюса до екватора, має траєкторію, що є чвертю великого кола Землі (рис. 1). Велике коло – це коло на поверхні Землі, центр якого збігається із центром Землі. Його радіус дорівнює радіусу Землі
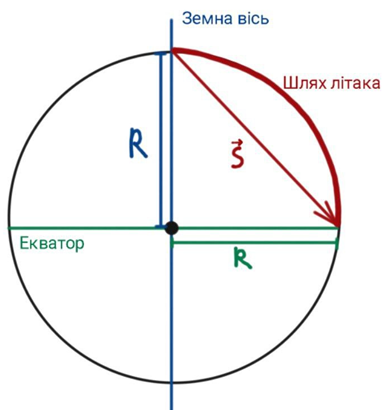
Рис. 1. Схема руху літака вздовж меридіана
Переміщення літака за цих умов – це хорда великого кола Землі. Її довжину можна дістати з теореми Піфагора:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики.
Завдання скеровано на перевірку вміння аналізувати графіки, що описують рух тіла.
Прямолінійний рух – це рух, траєкторію якого є пряма.
Щодо графіків у завданні:
А Це графік залежності проєкції швидкості
Б Це графік залежності координати
В Це графік залежності координати
Г Це графік залежності проекції швидкості
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА Механіка. Основи динаміки. Закони Ньютона.
Завдання скеровано на перевірку розуміння поняття інерціальної системи відліку та її складників.
Тіло відліку – це тіло, із яким в інерціальній системі відліку пов’язана система координат. Інерціальну систему відліку можна поєднати з тілом, що рухається без прискорення. В умові завдання єдиним тілом, яке рухається без прискорення, є шайба, що без тертя ковзає по льоду.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.
Завдання скеровано на перевірку розуміння понять роботи й потенціальної енергії пружини.
Робота, виконана пружиною під час розтягування чи стискання, дорівнює зміні потенціальної енергії пружини, узятій із протилежним знаком:
Потенціальну енергія пружини можна обчислити за формулою
Для обчислення потенціальної енергії пружини в кожному положенні необхідно перевести в метри видовження, подане в сантиметрах:
Тоді робота, яку пружина виконує під час скорочення від 4 см до 2 см, така:
А робота, яку пружина виконує під час скорочення від 2 см до 0 см, дорівнює:
Знак «мінус» у цьому разі означає, що пружина виконувала роботу, а не зовнішнє тіло виконувало роботу над нею.
Тож
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Одиниці фізичних величин.
Завдання скеровано на перевірку вміння визначати одиниці фізичних величин, записані в основних одиницях СІ.
А Роботу
Силу можна визначити згідно з другим законом Ньютона за формулою
Тож для розмірностей рівність така:
Б Потужність
1 Дж записано в одиницях СІ у варіанті A, тож для розмірностей рівність така:
В Момент сили М:
Г Імпульс сили
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на перевірку розуміння поняття кінетичної енергії та її зміни під час руху тіла унаслідок дії сили тяжіння.
Кінетичну енергію тіла визначають за формулою
Тіло, кинуте під кутом до горизонту, рухається внаслідок дії сили тяжіння, тобто з прискоренням, що дорівнює прискоренню вільного падіння.
Прискорення спрямоване вздовж осі
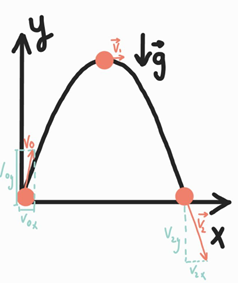
Рис. 1. Рух тіла, кинутого під кутом до горизонту
Модуль швидкості V в будь-який момент часу можна визначити за теоремою Піфагора:
Тож модуль швидкості й кінетична енергія тіла будуть найменшими тоді, коли проекція
У найвищій точці траєкторії тіло змінює напрямок свого руху: до цієї точки тіло піднімається і модуль
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.
Завдання скеровано на перевірку вміння аналізувати графіки ізопроцесів.
Тиск
Зміну температури можна визначити з рівняння стану:
На графіку, наведеному в умові, зображено цикл у координатах
1–2: ізобарне розширення (
Тож, якщо об’єм збільшується, а тиск залишається незмінним, то й температура збільшується.
2–3: ізотермічне стискання зі збільшенням тиску (
3–4: ізохорний процес зі зменшенням тиску (
Тож, якщо тиск зменшується, а об’єм залишається постійним, то й температура зменшується.
4–1: ізотермічне стискання зі збільшенням тиску (
А У процесі 2–3 температура зменшується, а повинна зростати.
Б У процесі 4–1 тиск зменшується, а має зростати.
В Цей графік є зображенням циклу в координатах
Г Процес 1–2 є ізотермічним, а повинен бути ізобарним.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.
Завдання скеровано на перевірку розуміння особливостей ізопроцесів.
Тиск
У герметично закритій кімнаті кількість речовини й об’єм сталі.
Унаслідок роботи обігрівача температура повітря в кімнаті зростатиме.
Із рівняння стану можна виразити тиск:
Тож, якщо температура зростає, а об’єм залишається незмінним, то тиск також зростатиме.
Тобто йдеться про ізохорний процес.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика й термодинаміка. Рівняння стану ідеального газу.
Завдання скеровано на перевірку розуміння особливостей ізопроцесів.
За графіком, наведеним в умові завдання, можна зробити висновок, що процес переводить газ зі стану з низьким тиском і малим об’ємом у стан із більшими тиском й об’ємом.
Тиск
Тож температуру можна виразити з рівняння стану:
Тобто внаслідок підвищення тиску й об’єму температура підвищується.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна та відносна вологість. Точка роси.
Завдання скеровано на оцінювання розуміння понять динамічної рівноваги й відносної та абсолютної вологості.
Точка роси – це температура, за якої водяна пара в повітрі стає насиченою.
Відносна вологість – фізична величина, яка показує, наскільки водяна пара близька до насичення. Відносна вологість дорівнює поданому у відсотках відношенню абсолютної вологості до густини насиченої водяної пари за цієї температури.
Абсолютна вологість – фізична величина, яка характеризує вміст водяної пари в повітрі й чисельно дорівнює масі водяної пари в повітрі об’ємом
Стан, за якого швидкості конденсації та пароутворення однакові, називають станом динамічної рівноваги.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Властивості газів, рідин і твердих тіл. Плавлення і твердіння тіл.
Завдання скеровано на перевірку розуміння механізмів кристалізації та конденсації.
Хмари утворюються тому, що тепле повітря має меншу густину, ніж холодне, тож воно швидко піднімається вгору. У вищих шарах атмосфери повітря адіабатно розширюється, що приводить до його охолодження.
Зі зниженням температури максимальна кількість води, яку може втримувати повітря зменшується. Тож водяна пара в повітрі, що швидко охолодилося під час піднімання, конденсується й утворюються крапельки води, сукупність яких і є хмарою.
За такої конденсації в хмарах майже немає пилинок чи інших частинок, які можуть стати центрами кристалізації. У такому разі рідина кристалізується за значно нижчих температур.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на перевірку розуміння понять потенціалу й еквіпотенціальних поверхонь.
Потенціал на поверхні провідника в усіх точках однаковий, тобто поверхня провідника є еквіпотенціальною.
Потенціал на поверхні металевої кулі визначають за формулою
Тож за однакових зарядів потенціал кулі з більшим радіусом є меншим за потенціал кулі з меншим радіусом.
З’єднані кулі утворюють один провідник, поверхня якого також має бути еквіпотенціальною, тож заряди перерозподіляться. Заряд від кулі з більшим потенціалом (малої кулі) перейде до кулі з меншим потенціалом (великої).
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку розуміння принципів підключення вимірювальних приладів в електричне коло.
Зазвичай у коло амперметр підключають послідовно, а вольтметр – паралельно (рис. 1).
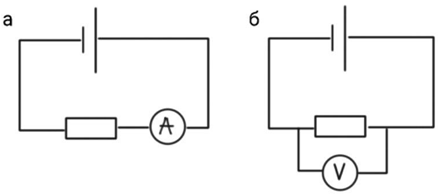
Рис. 1. Підключення в коло амперметра (а), вольтметра (б)
Нитка в лампі нагрівається за законом Джоуля:
Отже, що більша сила струму на лампочці, то більше розжарення її нитки.
Для розв’язання завдання потрібно зважити на закони послідовного (рис. 2) і паралельного (рис. 3) з’єднання провідників.
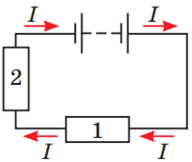
Рис. 2. Послідовне з’єднання провідників 1 і 2.
За послідовного з’єднання
Тож, щоб амперметр, уключений у коло послідовно, мало впливав на струм в колі, його опір має бути суттєво меншим за опір активних елементів (лампочки).
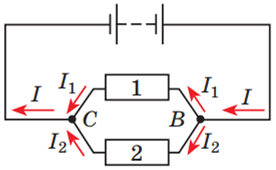
Рис. 3. Паралельне з’єднання провідників 1 і 2.
За паралельного з’єднання
За законом Ома
Тож, що більший опір провідника в паралельному підключенні, то менша сила струму через нього проходить. Для того, щоби вольтметр, підключений в коло паралельно, мало впливав на струм у колі, його опір повинен бути дуже великим.
Якщо замість вольтметра з великим опором підключити амперметр, опір якого дуже малий, то сила струму, що тече через прилад, буде більшою від очікуваної.
Сила струму в колі для паралельно підключених елементів дорівнює сумі сили струму в кожній гілці:
Тож, якщо силу струму в одній гілці збільшилася, то в іншій вона зменшиться. У результаті зменшення сили струму в лампочці зменшиться розжарення її нитки.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне та послідовне з’єднання провідників.
Завдання скеровано на перевірку знання закону Ома й розуміння особливостей паралельного та послідовного з’єднання провідників.
Схему з умови завдання доцільно перемалювати в зручнішому вигляді.
Точки контакту між двома провідниками можна рухати, тож варто перемістити вертикальний контакт, що підключає
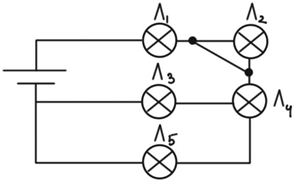
Рис. 1. Модифікована (1) схема умови задачі
Лампи
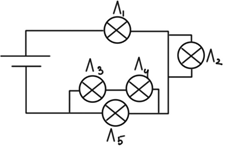
Рис. 2. Модифікована (2) схема умови задачі
Для розв’язання задачі потрібно взяти до уваги закони послідовного і паралельного з’єднання провідників.
За послідовного з’єднання (рис. 3)
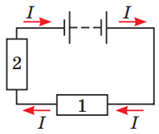
Рис. 3. Послідовне з’єднання провідників 1 і 2
За паралельного з’єднання (рис. 4)
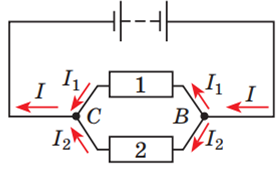
Рис. 4. Паралельне з’єднання провідників 1 і 2
Опір дротів між елементами настільки малий, що ним можна знехтувати під час розрахунків. Тож опір лампи
За законом Ома
Тож що більший опір провідника в паралельному підключенні, то менша сила струму через нього проходить. З огляду на різницю в опорі дротів і лампи струм через лампу
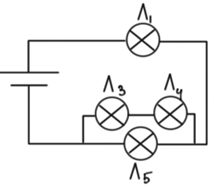
Рис. 5. Схема умови задачі
Яскравість лампи прямо пропорційна силі струму, що протікає крізь неї, тож для порівняння яскравості ламп досить порівняти силу струму, що протікає крізь них.
Нехай сила струму в колі дорівнює
За законом Ома
Тож
Усі лампи однакові, лампи
Тобто сили струму, що протікають крізь лампи, дорівнюють
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Магнітне поле, електромагнітна індукція.
Завдання скеровано на оцінку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.
Після замикання ключа
Права частина котушки підключена до негативного полюса джерела, а ліва – до позитивного. Струм у колі тече від + до –, тож він буде спрямований униз у ближній до спостерігача частині рисунка й угору в дальній частині.
Напрямок магнітного поля в котушці можна визначити за правилом правої руки (рис. 1):
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму в контурі, то відігнутий на
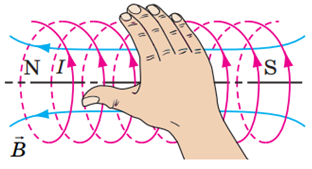
Рис. 1. Правило правої руки
Тобто для котушки в завданні також можна визначити напрямок ліній магнітної індукції, а отже і її магнітні полюси (рис. 2).
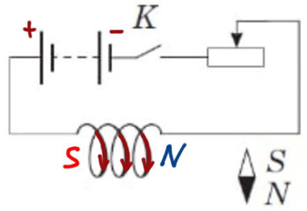
Рис. 2. Результат застосування правила правої руки
Магнітна стрілка на рисунку поруч із північним магнітним полюсом, тож вона повернеться до нього своїм південним полюсом.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.
Завдання скеровано на перевірку знання одиниць виміру для фізичних величин, пов’язаних із магнітним полем.
А Магнітну індукцію
Б Індуктивність
В Магнітний потік
Г Електроємність
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах.
Завдання скеровано на оцінювання розуміння механізмів різних видів газових розрядів.
Дуговий газовий розряд виникає за високої температури (понад
Іскровий газовий розряд виникає за атмосферного тиску й великої напруги між електродами. Його тривалість дуже мала, він має вигляд яскравих і розгалужених зиґзаґів.
Жеврійний (тліючий) газовий розряд виникає за невеликої напруги між електродами й низького тиску. Цей тип розряду приводить до жевріння в трубках із низьким тиском газу.
Коронний газовий розряд виникає за близького до атмосферного тиску в сильному
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника.
Завдання скеровано на перевірку вміння розв’язувати задачі про залежність періоду власних коливань системи від її параметрів.
Математичний маятник – це фізична модель коливальної системи з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля.
Характеристики коливань математичного маятника напряму залежать від його довжини. Зокрема, можна визначити період коливань математичного маятника
Нехай довжина маятника до укорочення дорівнювала
Після укорочення період
Частоту коливань маятника можна визначити за формулою
За умовою відомо, що до укорочення нитки частота коливань маятника
Тож період коливань після укорочення
А частота цих коливань
Тобто вкорочений маятник виконує 200 коливань за той самий інтервал часу.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механічні коливання і хвилі. Звукові хвилі.
Завдання скеровано на перевірку розуміння поняття звукової хвилі.
Звукові хвилі – це поздовжні механічні хвилі. Вони можуть поширюватися в будь-якому пружному середовищі (у газах, рідинах і твердих тілах).
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.
Завдання скеровано на перевірку розуміння джерел електромагнітних хвиль.
Джерелом електромагнітної хвилі може бути заряджене тіло, що рухається з прискоренням, або провідник зі змінним струмом.
Тож рівномірний рух частинок не може бути причиною виникнення електромагнітної хвилі.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Оптика. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку розуміння принципів побудови зображень у дзеркалі.
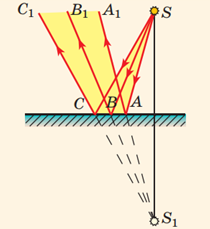
Рис. 1. Схема побудови зображення в дзеркалі
Відстань між дзеркалом й об’єктом дорівнює відстані між дзеркалом і зображенням.
Якщо тіло перебувало на відстані 15 см від дзеркала, то після того, як його відсунули, воно опинилося на відстані 30 см від дзеркала. На такій самій відстані буде і його зображення.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Елементи теорії відносності.
Завдання скеровано на перевірку розуміння постулатів спеціальної теорії відносності.
Постулати спеціальної теорії відносності:
1. В інерціальних системах відліку всі закони природи однакові.
2. Швидкість поширення світла у вакуумі однакова в усіх інерціальних системах відліку.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.
Завдання скеровано на оцінювання розуміння законів фотоефекту.
Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.
Закони фотоефекту
1. Кількість фотоелектронів, яку випромінює катод за одиницю часу, прямо пропорційна інтенсивності світла.
2. Максимальна початкова швидкість фотоелектронів збільшується зі збільшенням частоти падного світла й не залежить від інтенсивності світла.
3. Для кожної речовини є максимальна довжина світлової хвилі
За зіткнення фотона й електрона в катоді електрон поглинає енергію фотона, яку можна визначити за формулою
Ця енергія має бути витрачена на те, щоби вирвати електрон із поверхні катода (цю частку енергії називають роботою виходу
Що менша частота випромінювання і, відповідно, що більша його довжина хвилі, то меншу енергію
Якщо
Відповідь: A.
Знайшли помилку? Пишіть на
Квантова фізика. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з періодом піврозпаду.
Період піврозпаду
Тоді кількість ядер, що залишилася після розпаду, визначають за формулою
Після підставлення відомих з умови значень у формулу:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.
Завдання скеровано на перевірку розуміння зв’язку між силою, прискоренням і швидкістю руху тіла.
За другим законом Ньютона рівнодійна всіх сил, що діють на тіло, пов’язана з його прискоренням формулою
Тож напрямок прискорення збігається з напрямком дії сили.
1. Якщо сила весь час перпендикулярна до швидкості, то й прискорення перпендикулярне до неї. Прискорення, що перпендикулярне до швидкості, не змінює її модуля, але змінює її напрямок. Це відповідає рівномірному руху за криволінійною траєкторією, наприклад, руху по колу.
2. Якщо сила зберігає напрямок і величину незмінною, то й прискорення залишається незмінним. Оскільки напрямок швидкості відносно прискорення з умови невідомий, то визначити, збільшуватиметься чи зменшуватиметься модуль швидкості, неможливо. Тож це відповідає руху з постійним прискоренням.
3. Якщо напрямок сили, а отже й прискорення, збігається з напрямком швидкості, то модуль швидкості збільшується.
4. Якщо напрямок сили й прискорення протилежні до напрямку швидкості, то модуль швидкості зменшується.
Відповідь: 1В, 2Д, 3А, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Основи молекулярно-кінетичної теорії.
Завдання скеровано на перевірку розуміння формул, що стосуються молекулярно-кінетичної теорії (МКТ).
A
Б
B
Г
Д
Відповідь: 1А, 2Д, 3В, 4Б.
Знайшли помилку? Пишіть на
ТЕМА: Природні явища.
Завдання скеровано на перевірку вміння поєднувати фізичні явища з їхніми проявами в природі та використанням у техніці.
1. І під час дощу, і у зрошувальній системі краплі води рухаються під дією сили тяжіння.
2. У смерчі, пилососі й центрифузі використовують потоки рідин чи газів, що мають однакову форму.
3. У водоспаді та греблі електростанції потік води має майже однакову форму.
4. Полярне сяйво та світіння люмінесцентної трубки є проявом жеврійного (тліючого) газового розряду.
Відповідь: 1А, 2В, 3Б, 4Д.
Знайшли помилку? Пишіть на
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння основних величин, пов’язаних із коливаннями математичного маятника.
Тіло на довгій нитці можна вважати математичним маятником (рис. 1).
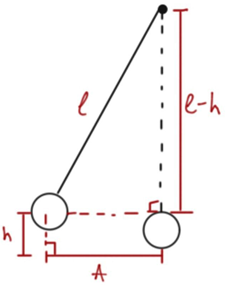
Рис. 1. Математичний маятник у положеннi максимального відхилення
1. Період коливань математичного маятника
2, 3. Енергію коливань можна визначити за формулою
У точці з найбільшим відхиленням потенціальна енергія тіла на підвісі максимальна, а кінетична енергія дорівнює
Максимальну висоту
За теоремою Піфагора
Якщо коливання малі, то й висота підйому
Тобто максимальна висота тягарця над нижньою точкою траєкторії залежить від
Енергія коливань
Тож енергія коливань пропорційна до
4. У найнижчій точці траєкторії потенціальна енергія тягарця дорівнює нулю, а його кінетична енергія, а отже й модуль швидкості, максимальні:
Тобто максимальна швидкість пропорційна до
Відповідь: 1В, 2А, 3Д, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Закони Ньютона.
Завдання скеровано на перевірку вміння розв’язувати задачі з динаміки з аналізом світлин експерименту.
За рисунком 1 легко визначити, що на лівій нитці блоку підчеплено п’ять тягарців із масою

Рис. 1. Сили, що діють на тягарці
1. Знайти:

Рис. 2. Сили, що діють на систему
Нерухомий блок – простий механізм, він не забезпечує виграшу ні в силі, ні у відстані, а лише змінює напрямок прикладання сили.
Оскільки сили
Запис другого закону Ньютона для тягарців із масою 5m і 3m відповідно:
Спроєктуймо рівняння на вертикальну вісь, спрямовану вниз. Для цього треба пригадати, що лівий вантаж рухається вниз, а правий – угору. Їхні прискорення мають такі самі напрямки:
Тож
Силу тяжіння можна розрахувати за формулою:
2. Знайти:
Маса одного тягарця дорівнює
З рівняння для другого закону Ньютона для вантажу масою
Відповідь: 1. 2,5. 2. 3,75.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика та термодинаміка. Рівняння стану ідеального газу. Відносна вологість.
Завдання скеровано на оцінювання вміння розв’язувати комбіновані задачі з використанням рівняння стану ідеального газу й формул, що стосуються вологості повітря.
Дано:
1. Знайти:
У рівняння стану ідеального газу треба підставити температуру в кельвінах (К):
Тоді з рівняння стану ідеального газу можна виразити масу газу:
2. Знайти:
Відносну вологість повітря можна визначити за формулою:
За умовою тиск насиченої пари води
Тож
Відповідь: 1. 0,48. 2. 100.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота та потужність електричного струму.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що стосуються роботи й потужності електричного двигуна.
Дано:
1. Знайти:
Потужність пов’язана з роботою формулою
Потужність електричного двигуна можна визначити за формулою
Тож:
2. Знайти:
ККД двигуна визначають як відношення корисної роботи, виконаної ним, до повної роботи:
Корисна робота – це робота, що необхідна для підйому вантажу на висоту 2 м.
Роботу сили можна визначити за формулою
Вважатимемо, що кут між напрямком сили й переміщенням вантажу дорівнює нулю, а переміщення тіла дорівнює висоті його підйому, тож
Вантаж втримується на землі завдяки силі тяжіння, тож піднімальна сила має за модулем дорівнювати їй:
Повна робота – це робота, виконана електричним двигуном, що була розрахована в попередньому пункті. Тоді:
Відповідь: 1. 60. 2. 80.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Поперечні та поздовжні хвилі. Довжина хвилі.
Завдання скеровано на перевірку вміння аналізувати графічні зображення хвиль.
1. Знайти:
Довжина хвилі
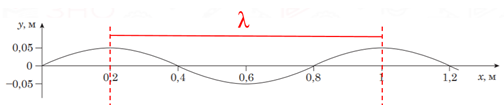
Рис. 1. Визначення довжини хвилі
Тоді
2. Знайти:
Період коливань поплавка збігається з періодом коливань частинок води у хвилі. Період коливання частинок і період хвилі також збігаються для будь-якої хвилі.
За один період гребінь хвилі переміститься на одну довжину хвилі, тож
Тоді період можна визначити за формулою
Відповідь: 1. 0,8. 2. 1,6.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Умова плавання тіл.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням закону Архімеда.
Дано:
Знайти:
На камінь у воді діють дві сили – сила тяжіння, що притягує його до дна, і виштовхувальна сила Архімеда (рис. 1).
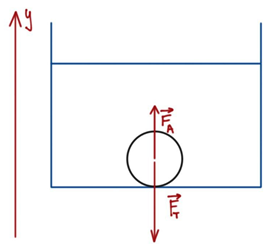
Рис. 1. Схема дії сил на камінь
Пригадаймо, що силу тяжіння можна визначити за формулою
Силу Архімеда можна визначити за формулою
Тоді можна записати другий закон Ньютона для каменя:
Спроєктуймо сили на вісь
Оскільки проєкція рівнодійної в цьому разі від’ємна, то сила тяжіння більша за виштовхувальну силу, що діє на камінь, тож камінь лежить у воді на дні.
Роботу сили можна визначити за формулою
За умови, що кут між напрямком сили й переміщенням каменя дорівнює нулю, а переміщення тіла дорівнює висоті його підйому
Робота, яку людина має виконати для піднімання тіла, – це робота проти рівнодійної сил, що діють на нього. Тому модуль піднімальної сили має дорівнювати модулю рівнодійної сил, що діють на камінь. Тоді роботу людини можна розрахувати за формулою:
Відповідь: 180
Знайшли помилку? Пишіть на
ТЕМА: Динаміка рідин і газів. Потужність.
Завдання скеровано на перевірку розуміння поняття потужності й динаміки потоку рідини в трубі.
Дано:
Знайти:
Водний насос, що перекачує воду, виконує роботу над нею. Оскільки труба горизонтальна, то під час руху нею потенціальна енергія води не змінюється. Робота, виконана над водою в трубі, переходить у її кінетичну енергію.
Тоді потужність водяного насоса
Маса й об’єм пов’язані між собою формулою
Маса води, що протікає крізь трубу, дорівнює добутку її густини на об’єм:
За умовою кількість води, що протікає по трубі, і, відповідно, її маса мають збільшитися вдвічі
Об’єм води, що протікає крізь трубу за час
Тоді потужність
Оскільки переріз труби не змінюється, то для збільшення об’єму води вдвічі має збільшитися вдвічі швидкість потоку:
Тоді відношення потужності до і після зміни таке:
Відповідь: 8.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика та термодинаміка. Рівняння теплового балансу.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння теплового балансу.
Дано:
Знайти:
Потенціальну енергію води на вершині водоспаду можна розрахувати за формулою
Під час падіння потенціальна енергія води зменшується і біля підніжжя дорівнює нулю. Тож кількість теплоти, витрачена на нагрівання води під час падіння дорівнює 60 % від потенціальної енергії на вершині:
Кількість витраченої на нагрівання теплоти пов’язана зі зміною температури формулою
Тоді можна скласти рівняння:
Відповідь: 0,02.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота й потужність електричного струму.
Завдання скеровано на перевірку розуміння поняття втрати напруги.
Дано:
Знайти:
Втрата напруги – це різниця між напругою на кінцях лінії:
Втрату напруги можна розрахувати за формулою
Опір провідника залежить від його геометричних характеристик:
Тоді
Потужність джерела пов’язана з напругою і силою струму:
Тоді, виразивши силу струму через потужність і напругу джерела, можна перетворити формулу для втрати напруги:
Тоді довжина провідника
Лінія електропередач має два кабелі, тому довжина одного з них дорівнюватиме половині загальної довжини провідника: 2,5 км.
Відповідь: 2,5.
Знайшли помилку? Пишіть на
ТЕМА: Електромагнітні коливання та хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули Томсона.
Дано:
Знайти:
Якщо вважати, що швидкість електромагнітної хвилі в повітрі дорівнює швидкості світла у вакуумі, то довжина випроміненої контуром хвилі пов’язана з періодом коливань цього контуру:
Період електромагнітних коливань в електричному контурі визначають за формулою Томсона:
Тоді індуктивність котушки можна визначити за формулою:
Відповідь: 9.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Світлові кванти.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули імпульсу фотона.
Дано:
Знайти:
Пригадаймо зв’язок імпульсу фотона та його довжини хвилі:
Коли фотон відбивається від ідеального дзеркала, то напрямок його руху змінюється на протилежний. За законом збереження імпульсу
Після удару фотон віддає дзеркалу імпульс p_max, до удару вважатимемо імпульс дзеркала нульовим:
Оскільки фотон повністю відбивається від дзеркала, то його імпульс змінює знак, але не модуль, тому:
Тоді довжина хвилі фотона
Відповідь: 660.
Знайшли помилку? Пишіть на




