ЗНО онлайн 2018 року з фізики – основна сесія

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух. Кінетична енергія.

Завдання скеровано на оцінювання вміння розраховувати кінетичну енергію для різних типів руху, зокрема рівноприскореного.

Кінетична енергія \(T\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси m тіла на квадрат швидкості v його руху: $$ T=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, а \(v\) – швидкість його руху.

Під час рівноприскореного руху залежність швидкості тіла від часу можна записати так: $$ v=v_0+at, $$ де \(v_0\) – початкова швидкість, а \(a\) – прискорення тіла.

Після підставлення виразу для швидкості рівноприскореного руху у вираз для кінетичної енергії можна дістати залежність кінетичної енергії від часу: $$ T=\frac{m(v_0+at)^2}{2}=\frac m2 (v^2_0+2v_0at+a^2t^2). $$

У виразі є \(t^2\) – час у квадраті. Тобто залежність має вигляд параболи. На рисунку єдиний проміжок, що не є прямою – це проміжок 2–3.

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Умови рівноваги.

Завдання скеровано на оцінювання вміння використовувати умови рівноваги для розв’язування розрахункових задач.

Важіль – це тверде тіло, яке може обертатися навколо нерухомої осі – осі обертання.

Важіль перебуває в рівновазі, якщо сума моментів сил, що діють на нього, дорівнює нулю.

Момент сили \(M\) – це фізична величина, що дорівнює добутку модуля сили \(F\), яка діє на тіло, на плече \(d\) цієї сили.

За рисунком до завдання можна визначити, що до правого плеча на відстані чотирьох поділок прикріплено три вантажі. Кожен із цих вантажів діє на плече із силою, що дорівнює їхній вазі.

На праве плече важеля на відстані трьох поділок прикріплено один вантаж, а на відстані двох поділок ми діємо силою.

Оскільки важіль за умовою перебуває в стані рівноваги, можна скористатися рівністю моментів сил: $$ 1)\ M_1=M_2, $$ де \(M_1\) і \(M_2\) – відповідні моменти сил: $$ 2)\ \left\{\begin{array}{l} M_1=l_1P_{3\ \text{вантажі}}=3l_1mg;\\ M_2=l_2F+l_3P_{1\ \text{вантаж}}=l_2F+l_3mg. \end{array}\right. $$

Вага трьох вантажів дорівнює сумі ваги кожного з них: $$ 3)\ \overrightarrow{P_3}=m\overrightarrow{g}+m\overrightarrow{g}+m\overrightarrow{g}=3m\overrightarrow{g}, $$ де \(l_1,\ l_2\) і \(l_3\) – відповідні плечі сил в умовних одиницях, позначені на рисунку 1.

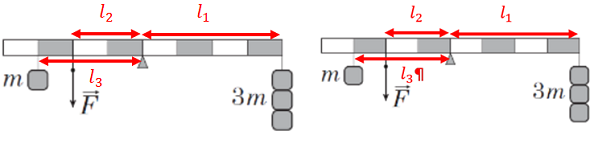
Рис. 1. Схематичний розподіл сил

Після підставлення виразу (2) у вираз (1): $$ 3)\ 3l_1mg=l_2F+l_3mg. $$ Оскільки масштаб в умові не зазначено, то вважатимемо, що поділка – це умовна одиниця довжини \(у. о. д\)..

Із (3) можемо виразити \(F\):

Відповідь: B.

ТЕМА: Механіка. Потенціальна енергія.

Завдання скеровано на оцінювання розуміння поняття потенціальної енергії і способів її обчислення для різних тіл

Потенціальна енергія \(U\) – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою.

Для тіл, що перебувають у полі сили тяжіння, потенціальну енергію визначають за формулою $$ U=mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.

Потенціальну енергію пружного тіла визначають за формулою \begin{gather*} U=\frac{kx^2}{2}, \end{gather*} де \(k\) – жорсткість тіла, \(x\) – його абсолютне видовження.

А Коли космічний корабель віддаляється від поверхні Землі, то він мусить виконувати роботу проти поля тяжіння Землі. У такому разі його потенціальна енергія зростає.

Б Коли контейнер піднімають на борт судна, то його висота над поверхнею землі збільшується, а отже й потенціальна енергія зростає.

В Коли тіло занурили у воду, то була виконана робота проти виштовхувальної сили. Тобто м’яч отримав додаткову енергію. Те саме відбувається із тілами, які піднімають на певну висоту (робота виконується проти поля сили тяжіння). Відразу після того, як сили перестають підтримувати тіло в положенні з більшою потенціальною енергією, воно починає рухатися до положення з найменшою потенціальною енергією. Саме тому, якщо тіло, підняте на висоту, відпустити, то воно падає. У цьому випадку тіло спливає, а його потенціальна енергія зменшується.

Г Коли спортсмен натягує тятиву, її абсолютне видовження \(x\) збільшується, а отже збільшується і її потенціальна енергія.

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення.

Завдання скеровано на оцінювання розуміння особливостей пружного зіткнення і вміння використовувати закони збереження.

Пружне зіткнення – це зіткнення, після якого сумарна кінетична енергія тіл зберігається: $$ W_{\text{кульки}}=\frac{mv^2}{2}. $$

Тож можна обчислити кінетичну енергію кожної з кульок до зіткнення. Нехай рухома кулька – кулька 1, а нерухома – 2: \begin{gather*} W_1=\frac{mv^2}{2}=\frac{m(10\ \frac{\text{м}}{\text{с}})^2}{2}=50m\ \text{Дж};\\[1pt] W_2=\frac{mv^2}{2}=\frac{m(0\ \frac{\text{м}}{\text{с}})^2}{2}=0\ \text{Дж}. \end{gather*}

Тоді сумарна кінетична енергія до зіткнення становить $$ W_{\text{до}}=W_1+W_2=50m\ \text{Дж}. $$

У замкнутій системі має зберігатися сумарний імпульс тіл. Імпульс першої кульки до зіткнення становить $$ p_1=mv=10m\ \text{кг}\cdot \text{м/с}. $$

Імпульс другої кульки: $$ p_2=mv=0\ \text{кг}\cdot \text{м/с}. $$

Тоді сумарний імпульс до зіткнення становить: $$ p_{\text{до}}=p_1+p_2=10m\ \text{кг}\cdot \text{м/с}. $$

У випадку A після зіткнення швидкості першої і другої кульки дорівнюють \(–10\ \text{м/с}\) і \(0\ \text{м/с}\) відповідно. Тоді сумарна кінетична енергія після удару становитиме:

Імпульс першої кульки до зіткнення становить $$ p_{1 А}=mv=-10m\ \text{кг}\cdot \text{м/с}. $$

Імпульс другої кульки $$ p_{2 А}=mv=0\ \text{кг}\cdot \text{м/с}. $$

Сумарний імпульс системи після зіткнення становить $$ p_{\text{після А}}=p_{1 А}+p_{2 А}=-10m\ \text{кг}\cdot \text{м/с}. $$

Отже імпульс не зберігається.

У випадку Б після зіткнення швидкості першої і другої кульки відповідно дорівнюють \(–5\ \text{м/с}.\) Тоді сумарна кінетична енергія після удару становитиме

Отже кінетична енергія після удару менша, ніж до нього. Зіткнення не пружне.

У випадку B після зіткнення швидкості першої і другої кульки відповідно дорівнюють \(-5\ \text{м/с}\) та \(5\ \text{м/с}.\) Тоді сумарна кінетична енергія після удару становитиме:

Отже кінетична енергія після удару менша, ніж до нього. Зіткнення не пружне.

У випадку Г після зіткнення швидкості першої і другої кульки дорівнюють \(0\ \text{м/с}\) і \(10\ \text{м/с}\) відповідно. Тоді сумарна кінетична енергія після удару становитиме

Імпульс першої кульки до зіткнення становить $$ p_{1 Г}=mv=0\ \text{кг}\cdot \text{м/с}. $$

Імпульс другої кульки дорівнює $$ p_{2 Г}=mv=10\ \text{кг}\cdot \text{м/с}. $$

Сумарний імпульс системи після зіткнення становить $$ p_{\text{після Г}}=p_{1 Г}+p_{2 Г}=10m\ \text{кг}\cdot \text{м/с}. $$

Отже імпульс і кінетична енергія зберігаються – зіткнення пружне.

Відповідь: Г.

ТЕМА: Гідростатичний тиск.

Завдання скеровано на оцінювання розуміння поняття гідростатичного тиску

У кожній із посудин, зображених на рисунку, рідина встановилася на однаковому рівні. Тиск на дно рідини складатиметься з атмосферного тиску, який буде однаковим для трьох посудин, що розташовані в тій самій кімнаті і тиску стовпчика рідини в посудині. Тиск нерухомого стовпчика рідини або газу називають гідростатичним.

Гідростатичний тиск \(p\) визначають за формулою $$ p=\mathbf{\rho}gh, $$ де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Оскільки висота стовпчика рідини в усіх посудинах однакова, то і їхній гідростатичний тиск також буде однаковим. А отже й загальний тиск на дно посудини буде однаковим.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані із середньою квадратичною швидкістю молекул.

Кількість зіткнень залежить від середньоквадратичної швидкості руху молекул: що більша швидкість їхнього руху, то частіше вони стикаються одні з одними й зі стінками.

За основним рівнянням молекулярно-кінетичної теорії існує зв’язок між макроскопічними параметри \(тиском, об’ємом і температурами\) і середньою швидкістю руху молекул у квадраті: $$ p=\frac 13 m_0n\overrightarrow{v^2}, $$ де \(p\) – тиск, \(m_0\) – маса однієї молекули, \(\overrightarrow{v^2}\) – середня швидкість молекул у квадраті, \(n\) – концентрація молекул. $$ n=\frac NV. $$ де \(N\) – кількість молекул, \(V\) – об’єм.

Тоді основне рівняння молекулярно-кінетичної можна переписати: $$ pV=\frac 13 m_0N\overrightarrow{v^2}. $$

З огляду на рівняння стану $$ pV=vRT. $$

Тому $$ vRT=\frac 13 m_0N\overrightarrow{v^2}. $$

Середньоквадратичну швидкість можна обчислити з виразу $$ v_{\text{кв}}=\sqrt{\overrightarrow{v^2}}. $$

Кількість речовини $$ v=\frac mM, $$ де \(M\) – молярна маса речовини, а \(m\) – маса тіла.

Зважаючи на те, що добуток маси однієї молекули на їхню кількість становить масу всього тіла, $$ m_0N=m. $$

Тому $$ \frac mM RT=\frac 13m\overrightarrow{v^2}. $$

Тобто $$ v_{\text{кв}}=\sqrt{\overrightarrow{v^2}}=\sqrt{\frac{3RT}{M}}. $$

Аби дізнатися, у скільки разів збільшиться кількість зіткнень зі стінкою за 1 с, необхідно обчислити, чому дорівнює відношення середньоквадратичної швидкості молекул за температури 1 000 К до середньоквадратичної швидкості молекул за температури 250 К: $$ \frac{v_{\text{кв 1000 К}}}{v_{\text{кв 2500 К}}}=\frac{\sqrt{\frac{3R\cdot 1000\ \text{К}}{M}}}{\sqrt{\frac{3R\cdot 250\ \text{К}}{M}}}=\sqrt{\frac{1000\ \text{К}}{250\ \text{К}}}=2. $$

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Ізотермічний процес – процес змінювання за незмінної температури стану газу деякої маси.

На графіках у завданні процеси зображено в координатах \(V\) і \(T\). У такому вигляді ізотермічний процес – це пряма, перпендикулярна до осі \(T.\)

Відповідь: A.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).

Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий у вологу тканину. Вода з тканини завжди випаровується, і швидкість випаровування залежить від того, яка вологість повітря навколо. Для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплено стрілку. Тому, коли кришка камери піднімається чи опускається, пружина деформується, а стрілка починає рухатися по шкалі.

Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується: $$ F=kx. $$

Тому, якщо відомий коефіцієнт жорсткості пружини, то за значенням її видовження можна визначити й силу, що його зумовлює.

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.

Завдання скеровано на оцінювання розуміння понять динамічної рівноваги й відносної й абсолютної вологості.

Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.

Відносна вологість – фізична величина, яка показує, наскільки водяна пара близька до насичення, і дорівнює поданому у відсотках відношенню абсолютної вологості до густини насиченої водяної пари за певної температури.

Абсолютна вологість – фізична величина, яка характеризує вміст водяної пари в повітрі й чисельно дорівнює масі водяної пари, що міститься в повітрі об’ємом \(1\ \text{м}^3.\)

Стан, за якого швидкості конденсації і пароутворення однакові – це стан динамічної рівноваги.

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Капілярні явища.

Завдання скеровано на оцінювання розуміння загальних принципів капілярних явищ.

Висоту підйому або опускання води в капілярі порівняно з рівнем води в широкій посудині обчислюють за формулою: $$ h=\frac{2\mathbf{\sigma}}{\mathbf{\rho}gr} . $$ \(\mathbf{\sigma}\) – поверхневий натяг рідини, \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, а \(r\) – радіус капіляра.

Вода змочує скло, тому вона підніматиметься в капілярах.

Поверхневий натяг мильного розчину становить \(0,04\ \text{Н/м}\), а води – \(0,07\ \text{Н/м}\), тому якщо у воду додати мило, то її поверхневий натяг зменшиться. А отже зменшиться висота її підйому в капілярі.

Зі збільшенням температури поверхневий натяг зменшується, адже більше молекул пари опиняється поруч із поверхнею рідини. Що більше молекул газу опиняється поруч із поверхнею, то ближчими будуть сумарні сили взаємодії молекул рідини на поверхні з молекулами газу й молекулами рідини. А отже рівнодійна, що затягує молекули на поверхні вглиб об’єму рідини буде меншою, що й зменшує поверхневий натяг. Тож зі збільшенням температури зменшиться і висота підйому рідини в капілярі.

Ширина посудини з водою ніяк не впливає на підйом рідини всередині капіляра.

Тонший капіляр має менший радіус. Що менший радіус капіляра, то вища висота підйому рідини в ньому.

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.

Завдання скеровано на оцінювання розуміння напруженості електричного поля і вміння порівнювати її в різних точках електричного поля.

Напруженість електричного поля в певній точці \(\overrightarrow{E}\) – векторна фізична величина, яка характеризує електричне поле й дорівнює відношенню сили \(\overrightarrow{F},\) із якою електричне поле діє на пробний заряд \(q\), поміщений у цю точку поля, до значення цього заряду $$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q}. $$

На пробний заряд \(q\) з боку поля діє сила Кулона, яка за модулем дорівнює $$ F=k\frac{|Q||q|}{r^2}, $$ де \(r\) – відстань між зарядами, а \(k=9\cdot 10^9\ \text{Нм}^2/\text{Кл}^2\).

Тоді модуль напруженості електричного поля дорівнюватиме $$ E=k\frac{|Q|}{r^2}. $$

Оскільки масштаб рисунку невідомий, то можна вважати, що клітинка дорівнює умовній одиниці довжини \(у. о. д\).. Відстань до точки 1 становить 1 у. о. д. і 2 у. о. д. від кожного із зарядів відповідно. Відстань до точки 2 становить 6 у. о. д. і 3 у. о. д. від кожного із зарядів відповідно.

Напруженості електричного поля різних зарядів додають векторно, тому для точки 1 поле створене обома зарядами буде спрямоване у протилежні боки. Вважатимемо, що напрямок зліва направо – додатний, тоді загальна напруженість електричного поля в точці 1 становитиме:

А для точки 2 поля, створені обома зарядами, спрямовані в один бік, тому загальна напруженість становить

Тоді можемо знайти відношення напруженості електрично в кожній із точок:

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на оцінювання розуміння залежності ємності конденсатора від його геометричних параметрів.

На рисунку зображено плоский конденсатор. Вираз для його електроємності такий: $$ C=\frac{\mathbf{\varepsilon}_0\mathbf{\varepsilon}S}{d}. $$

Зміщення пластин одна відносно одної і їхній поворот не впливають на ємність конденсатора.

Зменшення відстані між пластинами її збільшить, а збільшення – зменшить.

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання розуміння впливу струму на середовища, у яких він протікає.

Теплова дія струму полягає в тому, що будь-який провідник нагрівається під час проходження ним струму. Електрони, що рухаються під дією поля, зіштовхуються із частинками у кристалічній ґратці провідника. У результаті таких зіткнень частинки поглинають кінетичну енергію електронів, внутрішня енергія провідника росте, а отже збільшується і температура.

Електроплита працює саме завдяки цьому ефекту: металеві конфорки або спіралі нагріваються, коли по них тече струм, що й дає змогу готувати на них їжу.

У випадку Б ілюстровано йонну провідність електролітів, а у випадках В і Г – появу магнітного поля у провідниках зі струмом.

Відповідь: A.

ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на оцінювання розуміння законів руху заряджених частинок в електричному полі.

На рухому заряджену частинку в полі діє сила Лоренца. Саме вона й зумовить зміну напрямку руху електрона, що рухається в однорідному магнітному полі. Сила Лоренца залежить від заряду частинки, її швидкості, індукції магнітного поля і кута, який утворюють напрямок швидкості й лінії магнітної індукції: $$ F=Bvq\sin\mathbf{\alpha}, $$ де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і напрямком руху частинки.

Якщо траєкторія електрона прямолінійна, то сила Лоренца не впливає на його рух, а отже має дорівнювати 0. Сила Лоренца дорівнюватиме нулю, коли \(\sin\mathbf{\alpha} = 0\). Тобто коли \(\mathbf{\alpha}=\mathbf{\pi}n\). Тож напрямок швидкості електрона має бути або співнапрямлений із напрямком ліній магнітної індукції, або протилежно напрямлений.

Тому, якщо лінії магнітної індукції напрямлені вертикально, то й електрон має рухатися в такому напрямку.

Відповідь: Г.

ТЕМА: Електродинаміка. Закони постійного струму.

Завдання скеровано на оцінювання розуміння поняття сторонніх сил і принципів роботи основних елементів електричного кола.

Сторонні сили – це будь-які не кулонівські сили, що діють на електрично заряджені частинки.

Джерела електричного струму повинні виштовхувати електрони в електричне коло. Вони мають позитивно й негативно заряджені полюси. Електрони рухаються від негативного полюса до позитивного по провідниках у колі. Проте відстань між двома полюсами джерела набагато менша, ніж довжина будь-якого кола. Частинки, що притягуються, завжди рухаються за найкоротшим шляхом. Тож чому електрони взагалі покидають джерело струму й опиняються в колі, а не просто рухаються в межах джерела?

В усіх джерелах діють сторонні сили, що змушують електрони рухатися до негативно зарядженого полюса. Сторонні сили протидіють кулонівським у джерелі, що прагнуть перемістити електрони до позитивно зарядженого полюса. Схематично дію сторонніх і кулонівських сил у джерелі струму зображено на рисунку 1. Стрілками синього кольору позначено кулонівські сили, а червоного – сторонні.

Тож джерело струму не може працювати без дії сторонніх сил всередині.

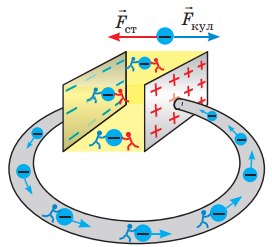
Рис. 1. Схематичне зображення дій сторонніх та кулонівських сил у джерелі струму

Відповідь: В.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на оцінювання розуміння понять магнітної індукції, індуктивності, магнітного потоку й магнітної проникності середовища.

Магнітна індукція \(B\) – векторна фізична величина, що характеризує силову дію магнітного поля $$ B=\frac{F_A}{Il}, $$ де \(I\) – сила струму в провіднику, \(l\) – довжина провідника, \(F_A\) – сила Ампера.

Індуктивність \(L\) – фізична величина, яка характеризує провідник і чисельно дорівнює електрорушійній силі (ЕРС) самоіндукції, що виникає в провіднику в разі зміни сили струму на 1 ампер за 1 секунду: $$ L=\frac{|\mathbf{\varepsilon}_{is}|\triangle t}{|\triangle I|}, $$ де \(\mathbf{\varepsilon}_{is}\) – ЕРС самоіндукції, \(\triangle I\) – зміна сили струму, \(\triangle t\) – проміжок часу, за який відбулася зміна струму.

Магнітний потік \(\boldsymbol Ф\) – це фізична величина, яка дорівнює добутку магнітної індукції \(B\) на площу \(S\) поверхні й на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю до поверхні: $$ \boldsymbol Ф=BS\cos\mathbf{\alpha}, $$ де \(B\) – магнітна індукція, \(S\) – площа поверхні, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і нормаллю до поверхні.

Магнітна проникність середовища \(\mathbf{\mu}\) – це фізична величина, яка характеризує магнітні властивості: $$ \mathbf{\mu}=\frac{B}{B_0}, $$ де \(B\) – магнітне поле в середовищі, \(B_0\) – магнітне поле у вакуумі.

Відповідь: A.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на оцінювання розуміння природи кінетичної і потенціальної енергії і вміння використовувати закони збереження повної механічної енергії.

У замкненій системі зберігається повна механічна енергія: $$ W=W_k+W_n=const. $$

Кінетичну енергію визначають за формулою $$ W_k=\frac{mV^2}{2}, $$ де \(m\) – маса тіла.

Оскільки для гумової стрічки виконуваний закон Гука, то можна обчислити потенціальну енергію за формулою, що описує потенціальну енергію розтягнутої пружини: $$ W_n=\frac{k\triangle x^2}{2}, $$ де \(k\) – коефіцієнт жорсткості пружини, а \(\triangle x\) – розтяг або стиск пружини.

Коли пружина стискається, то її потенціальна енергія збільшується, а отже, за законом збереження механічної енергії, кінетична енергія зменшується.

Вираз для сили пружності: $$ F_{\text{пруж}}=k\triangle x. $$

Отже, якщо пружина стискається, то й модуль сили пружності теж збільшується.

Прискорення тіла в положенні рівноваги дорівнює нулю, і чим більше тіло відхиляється він нього, тим більшим є його модуль. Тож під час стискання модуль прискорення збільшується.

Відповідь: A.

ТЕМА: Механічні коливання і хвилі. Звукові хвилі. Ехолокація.

Завдання скеровано на оцінювання розуміння принципів ехолокації і вміння розв’язувати відповідні розрахункові задачі.

Ехолоти посилають короткі ультразвукові імпульси в напрямку, у якому проводять дослідження. Ультразвукова хвиля відбивається від морського дна й повертається до ехолота. Ехолот фіксує час, за який хвиля повернулась, а отже подолала дві відстані – від ехолота до об’єкта й від об’єкта знову до ехолота.

Тому відстань до об’єкта можна розрахувати за формулою $$ S=\frac{vt}{2}, $$ де \(v\) – швидкість поширення звуку в середовищі, де проводили дослідження. За умовою \(v=1\ 400\ \text{м/с},\ t=0,6\ \text{с}\). Тоді $$ S=\frac{vt}{2}=\frac{1\ 400\ \frac{\text{м}}{\text{с}}\cdot 0,6\ \text{с}}{2}=420\ \text{м}. $$

Відповідь: Г.

ТЕМА: Магнітне поле, електромагнітна індукція. Трансформатор.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що ґрунтується на розумінні принципів роботи трансформатора.

Трансформатор – електромагнітний пристрій, що перетворює змінний струм однієї напруги на змінний струм іншої напруги за незмінної частоти.

Тож збільшується саме значення напруги змінного струму.

Відношення кількості витків у первинній обмотці до кількості витків у вторинній обмотці – це коефіцієнт трансформації. За умовою кількість витків у вторинній обмотці в \(n\) разів більша, ніж у первинній, тому можна розрахувати коефіцієнт трансформації: $$ k=\frac{N_{\text{перв}}}{N_{\text{втор}}}=\frac 1n. $$

Так само коефіцієнт трансформації можна визначити як відношення початкової напруги змінного струму до кінцевої: $$ k=\frac{U_1}{U_2}=\frac 1n. $$

Тоді $$ U_2=nU_1. $$

Відповідь: A.

ТЕМА: Оптика. Прямолінійність поширення світла в однорідному середовищі.

Завдання скеровано на оцінювання розуміння принципів прямолінійного поширення світла і їхнього зв’язку з фазами Місяця.

Повний місяць спостерігають тоді, коли освітлену частину Місяця повністю видима на неосвітленій частині Землі. Освітлена частина Місяця на рисунку позначена світло-сірим, а неосвітлену – темно-сірим.

У випадках А і В лише половина освітленої частини Місяця видима на Землі. Це перша й остання чверть місячної фази відповідно. У випадку Б освітлену частину видно повністю – це повний місяць. У випадку Г видно менше половини освітленої частини Місяця – це також остання чверть місячної фази.

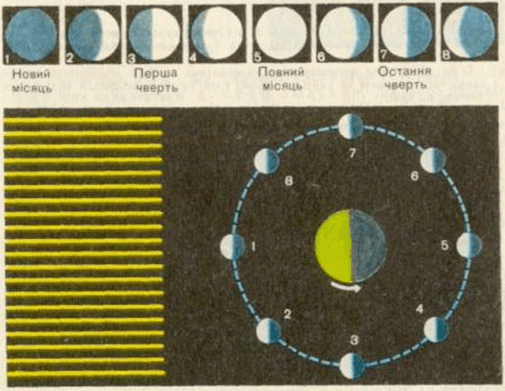
Рис. 1. Місячні фази залежно від положення Місяця (біло-синє коло) відносно Землі (жовто-синє коло) і Сонця (сонячні промені позначено жовтими лініями)

Відповідь: Б.

ТЕМА: Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням релятивістського закону додавання швидкостей.

Обидві частинки рухаються зі швидкістю, порівнюваною зі швидкістю світла. Тому в цьому разі для додавання швидкостей необхідно використовувати релятивістський закон: $$ v=\frac{v_1+v_2}{1+\frac{v_1v_2}{c^2}}, $$ де \(v\) – швидкість руху тіла відносно нерухомої системи відліку (К), \(v_1\) – швидкість руху тіла відносно рухомої системи відліку, \(v_2\) – швидкість рухомої системи відліку К'.

У цьому випадку нерухома система відліку К – це адронний колайдер \(на рисунку 1 позначено чорним кольором\). Рухому систему координат К' варто «прив’язати» до одного з ядер \(на рисунку 1 позначено синім кольором\). Інше ядро тоді можна вважати рухомим тілом у цих системах координат \(на рисунку 1 позначено червоним кольором\).

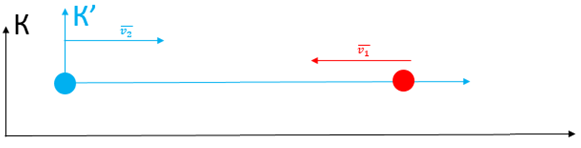
Рис. 1. Схема руху протонів в адронному колайдері

За умовою відомі швидкості руху ядер в адронному колайдері, тобто це швидкість v руху тіла відносно нерухомої системи координат і швидкість \(v_2\) рухомої системи координат К' відносно нерухомої.

Тоді, щоби знайти швидкість руху одного ядра відносно іншого, необхідно знайти швидкість руху тіла відносно рухомої системи координат (\(v_1\)). Виразимо швидкість \(v_1\) із виразу для релятивістського додавання швидкостей:

Тож одне з ядер рухалось назустріч іншому зі швидкістю \(0,8c\).

Відповідь: B.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання розуміння законів фотоефекту.

Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.

За першим законом фотоефекту кількість фотоелектронів, що їх випромінює катод за одиницю часу, прямо пропорційна інтенсивності світла.

За умовою завдання потужність джерела зменшилася вдвічі, а отже й інтенсивність випромінювання змінилася так само. Тоді за першим законом фотоефекту кількість випромінених електронів також зменшиться вдвічі.

Відповідь: B.

ТЕМА: Квантова фізика. Атом і атомне ядро. Радіоактивність.

Завдання скеровано на оцінювання розуміння поняття напіврозпаду.

Період піврозпаду \(T_{1/2}\) – це фізична величина, що характеризує радіонуклід і дорівнює часу, протягом якого розпадається половина наявної кількості ядер цього радіонукліда.

Тоді кількість ядер, що залишилася після розпаду, можна визначати за формулою $$ N=N_02^{\frac{t}{T_{1/2}}}, $$ де \(N\) – кількість ядер, що залишилася після розпаду, \(N_0\) – початкова кількість ядер, \(t\) – час розпаду.

Якщо за час \(t\) розпалося 75 % ядер, то після розпаду залишиться ще 25 % ядер: $$ N=0,25N_0=\frac 14N_0. $$

Тож можна використати таке відношення: $$ \frac{N}{N_0}=2^{\frac{t}{T_{1/2}}}=\frac{\frac 14N_0}{N_0}=\frac 14. $$

Тоді $$ 2^{\frac{t}{T_{1/2}}}=\frac 14=2^{-2}. $$

Якщо значення чисел зі степенями рівні й основи цих чисел рівні, то й степені цих чисел теж рівні: $$ -\frac{t}{T_{1/2}}=-2. $$

Тому $$ t=2T_{1/2}=2\cdot 1600\ \text{років}=3200\ \text{років} $$

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.

Завдання скеровано на оцінювання вміння визначати напрямок прискорення і швидкості в різних процесах.

А Снаряд, випущений гарматою чи будь-яким іншим способом, рухатиметься під дією сили тяжіння після вистрілу. У такому разі прискорення, що діє на тіло, – це прискорення вільного падіння, що завжди напрямлене до центра Землі. Тобто якщо поверхня горизонтальна, то прискорення вільного падіння спрямоване перпендикулярно до поверхні. Тіло в такому разі рухається по параболі. Схематичне зображення руху тіла, кинутого під кутом до горизонту, тобто руху снаряду, зображено на рисунку 1. Стрілкою червоного кольору позначено прискорення тіла, зеленого – напрямок швидкості тіла (напрямок руху). Кут між цими напрямками гострий.

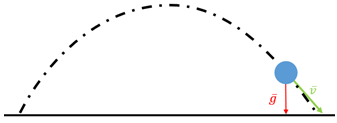
Рис. 1. Схематичне зображення руху снаряду перед падінням

Б Кінець годинникової стрілки рівномірно рухається по колу. За визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.

Під час руху по колу швидкість тіла постійно напрямлена по дотичній до кола. Це значить, що напрямок швидкості руху тіла постійно змінюється, але оскільки рух рівномірний, то модуль швидкості має залишатися постійним. Це можливо лише якщо прискорення напрямлене перпендикулярно до швидкості тіла. На рисунку 2 схематично зображено рух кінця годинної стрілки (позначеного синім кругом на рисунку). Тож кут між напрямком руху тіла й прискоренням у цьому разі завжди прямий.

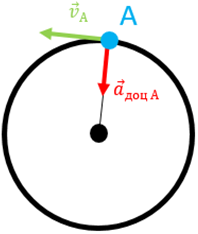
Рис. 2. Схематичне зображення руху кінця годинникової стрілки

В Під час руху снаряда в каналі ствола гармати його швидкість збільшується. Тобто прискорення співнапрямлене зі швидкістю тіла.

Г Після вимикання двигуна катера його швидкість починає зменшуватися. Тобто прискорення протилежно напрямлене до швидкості тіла.

Відповідь: 1Г, 2Д, 3В, 4А.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання знання вимірювальних пристроїв і розуміння фізичних величин, для вимірювання яких їх використовують.

1. Фізична величина, що дорівнює відношенню шляху до часу – це швидкість: $$ v=\frac St, $$ де \(S\) – шлях, \(t\) – час.

Прилад, що вимірює швидкість – це спідометр.

2. Фізична величина, що дорівнює добутку густини, прискорення вільного падіння і висоти стовпчика рідини – це гідростатичний тиск (тиск нерухомого стовпчика рідини): $$ p=\mathbf{\rho}gh, $$ де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Прилад, що вимірює тиск рідини чи газу – це манометр.

3. Фізична величина, що дорівнює відношенню густини водяної пари до густини насиченої пари за певної температури й виражена у відсотках – це відносна вологість: $$ \mathbf{\varphi}=\frac{\mathbf{\rho}}{\mathbf{\rho}_{\text{н}}}\cdot 100\ \text{%}, $$ де \(\mathbf{\rho}\) – густина водяної пари за певної температури, \(\mathbf{\rho}_{\text{н}}\) – густина насиченої пари.

Прилад, що вимірює відносну вологість – це гігрометр.

4. Фізична величина, що дорівнює добутку маси на прискорення вільного падіння – це сила тяжіння: $$ F_{\text{тяж}}=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Прилад, що вимірює силу – це динамометр.

Відповідь: 1В, 2А, 3Г, 4Б.

ТЕМА: Оптика. Інтерференція світла. Дисперсія світла. Поляризація світла.

Завдання скеровано на оцінювання вміння розпізнавати оптичні явища у природних явищах і сучасній техніці.

1. Бензин на асфальті утворює тонку прозору плівку, коефіцієнт заломлення у якої відрізняється від коефіцієнту заломлення повітря. Тож частина сонячних променів відбивається на межі бензин – повітря, а частина заломлюється і відбивається вже від поверхні бензин – асфальт (рисунок 1). Так між цими частинами проміння утворюється різниця ходу. Обидві частини мають одне джерело, тож вони є когерентними й відбувається інтерференція.

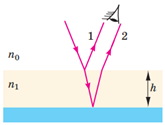
Рис. 1. Схема ходу променів під час інтерференції у плівці бензину

2. Туман виникає тоді, коли водяна пара в повітрі конденсується й утворюється багато водяних крапель. На кожній із них світло розсіюється й утворюється ореол.

3. Біле (сонячне) світло складається із хвиль із різними частотами. Показник заломлення для кожної з таких хвиль трохи відрізняється, тож кут заломлення після проходження крізь поверхню призми для них теж відрізнятимуться. У такий спосіб утворюється кольоровий спектр, як це зображено на рисунку 2.

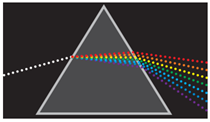
Рис. 2. Утворення дисперсійного спектра

4. Під час перегляду стереофільмів одночасно транслюють дві версії фільму, зняті під невеликим кутом одна до одної. Версії для кожного ока мають різну поляризацію, тому окуляри з поляризаторами дають змогу блокувати зображення, зняте для лівого ока на правому, і навпаки. Після цього, мозок обробляє два різнi зображення, отримані з двох очей, і «збирає» об’ємну картину.

Відповідь: 1В, 2А, 3Д, 4Б.

ТЕМА: Квантова фізика. Атом i атомне ядро. Альфа-, бета- і гамма-випромінювання.

Завдання скеровано на оцінювання розуміння природи радіоактивного випромінювання.

1. \(\mathbf{\alpha}\)-промені – це потік частинок, що складаються з 2 протонів i 2 нейтронів (ядра атомів Гелію).

2. \(\mathbf{\beta}\)-промені – це потік швидких електронів або позитронів.

3. \(\mathbf{\gamma}\)-промені – це електромагнітне випромінювання надзвичайно високої частоти, що утворюється під час ядерних реакцій.

4. Світлове випромінювання – це потік фотонів із частотами \(7,5\cdot 10^{14}–4\cdot 10^{14}\ \text{Гц}\). Вони утворюються під час переходу атомів зі збудженого стану в рівень із меншою енергією.

Відповідь: 1В, 2Б, 3А, 4Г.

ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Гука.

1. Знайти:
\(k\ -\ ?\)

Оскільки прикладена сила – розтягувальна, то довжина пружини збільшувалась. Під час розтягування в пружині виникає сила пружності, що й дорівнює силі розтягування: $$ F=F_{\text{пр}}. $$

Сила пружності пов’язана з абсолютним видовженням і коефіцієнтом жорсткості: $$ F_{\text{пр}}=kx, $$ де \(k\) – коефіцієнт жорсткості, \(x\) – абсолютне видовження пружини.

Тоді можна записати вираз для сили пружності в обох випадках: \begin{gather*} F_{\text{пр}\ 1}=kx_1,\\[7pt] F_{\text{пр}\ 2}=kx_2. \end{gather*}

Зважаючи на те, що максимальна довжина пружини в першому експерименті – 10 см, а в другому – 11 см, то можна записати зв’язок між абсолютними видовженнями в обох випадках (абсолютні видовження подано в метрах): \begin{gather*} x_2=x_1+0,01\ \text{м}. \end{gather*}

Тоді \begin{gather*} F_{\text{пр}\ 1}=kx_1,\\[7pt] F_{\text{пр}\ 2}=k(x_1+0,01\ \text{м}). \end{gather*}

Можна виразити абсолютне видовження \(x_1\) із виразу для першого експерименту й підставити його у вираз для другого:

Отже

2. Знайти:
\(l_0\ -\ ?\)

З виразу для сили пружності можна обчислити абсолютне видовження пружини для першого експерименту: \begin{gather*} F_{\text{пр}\ 1}=kx_1,\\[7pt] x_1=\frac{k}{F_{\text{пр}\ 1}}=\frac{3\ \text{Н}}{200\ \frac{\text{Н}}{\text{м}}}=0,015\ \text{м}. \end{gather*}

Тож, якщо максимальна довжина пружини в цьому експерименті – 10 см (0,1 м), то можна обчислити початкову довжину:

Відповідь: 1. 200. 2. 8,5.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу. Робота. Потужність. ККД.

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі, що поєднують у собі використання понять роботи, потужності й рівняння теплового балансу.

Дано:
\(V=10\ \text{л}\)
\(\triangle t=45\ ^\circ\text{С}\)
\(P=35\ \text{кВт}\)
\(c=4\ 200\ \text{Дж}/(\text{кг}\cdot \text{К})\)
\(\mathbf{\rho}=1\ 000\ \text{кг/м}^3\)

1. Знайти:
\(Q\ -\ ?\)

Кількість теплоти, що необхідна для нагрівання цієї порції води, можна обчислити з виразу: $$ Q=cm\triangle t. $$

Масу води можна обчислити за виразом:

Тоді можна обчислити кількість теплоти:

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

Коефіцієнт корисної дії (ККД) можна визначити як відношення корисної роботи \(A\) до загальної енергії \(Q\), виробленої газовим котлом: $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}. $$

Корисна робота газового котла в цьому разі – це кількість теплоти, витрачена на нагрівання води.

Загальну енергію, вироблену газовим котлом, можна обчислити з виразу для його потужності: $$ P=\frac{Q}{t}, $$ де \(Q\) - вироблена газовим котлом енергія, а \(t\) – час роботи газового котла. \begin{gather*} Q=Pt=35\ \text{кВт}\cdot 1\ \text{хв}=35\ 000\ \text{Вт}\cdot 60\ \text{с}=\\[7pt] =2\ 100\ 000\ \text{Дж}=2\ 100\ \text{кДж}. \end{gather*}

Тоді можна визначити ККД газового котла:

Відповідь: 1. 1890. 2. 90.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота і потужність електричного струму.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що стосуються залежності опору провідника від його геометричних параметрів і впливу змін опору провідника на потужність електричного струму.

Дано:
\(\triangle l=20\ \text{%}\)
\(U\) – стала

1. Знайти:
\(\frac{R_{\text{до}}}{R_{\text{після}}}\ -\ ?\)

Опір провідника залежить від його геометричних параметрів і матеріалу: $$ R=\mathbf{\rho}\frac lS, $$ де \(\mathbf{\rho}\) – питомий опір матеріалу, \(l\) – довжина провідника, \(S\) – площа перерізу провідника.

Якщо \(\triangle l\ –\ 20\ \text{%}\), то довжина після вкорочення становить \(80\ \text{%}\): $$ \frac{l_{\text{після}}}{l_{\text{до}}}=0,8. $$

Тоді можна обчислити зменшення опору після вкорочення: $$ \frac{R_{\text{до}}}{R_{\text{після}}}=\frac{\mathbf{\rho}\frac{l_{\text{до}}}{S}}{\mathbf{\rho}\frac{l_{\text{після}}}{S}}=\frac{l_{\text{до}}}{l_{\text{після}}}=\frac{1}{0,8}=1,25. $$

2. Знайти:
\(\triangle P\ (\text{%})\ -\ ?\)

Потужність нагрівника можна обчислити за формулою: \begin{gather*} P=UI, \end{gather*} де \(U\) – напруга, \(I\) – сила струму.

За законом Ома напруга, сила струму й опір ділянки кола пов’язані між собою: $$ I=\frac UR. $$

Тоді, зважаючи на те, що ніяких відомостей про силу струму умові не дано, можна підставити вираз закону Ома у вираз для потужності: \begin{gather*} P=\frac{U^2}{R}. \end{gather*}

Тоді, зважаючи на те, що напруга залишилась сталою, можна обчислити, на скільки відсотків збільшилася потужність після вкорочення спіралі: $$ \frac{P_{\text{після}}}{P_{\text{до}}}=\frac{\frac{U^2}{R_{\text{після}}}}{\frac{U^2}{R_{\text{до}}}}=\frac{R_{\text{до}}}{R_{\text{після}}}=1,25. $$

Тоді

Тобто потужність збільшилася на 25 %.

Відповідь: 1. 1,25. 2. 25.

ТЕМА: Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на оцінювання розуміння принципів роботи коливального контуру й уміння розв’язувати розрахункові задачі на зв’язок періоду й частоти коливань.

Дано:
\(\mathbf{\nu}= 1\ \text{кГц}\)

1. Знайти:
\(T(\text{с})\ -\ ?\)

Між періодом і частотою коливань існує зв’язок: $$ T=\frac{1}{\mathbf{\nu}}=\frac{1}{1\ \text{кГц}}=\frac{1}{1\ 000\ \text{с}^{-1}}=0,001\ \text{с}. $$

2. Знайти:
\(N\ (\text{разів за секунду}\ I=0)\ -\ ?\)

За один період у коливальному контурі заряд з одної обкладинки конденсатора протікає через котушку на іншу обкладинку, а потім назад. Тож за один період сила струму в котушці дорівнює нулю двічі: на початку періоду й у момент \(T/2\). Якщо за один період сила струму в котушці дорівнює нулю двічі, то кількість таких ситуацій за секунду дорівнює подвоєній частоті коливань: $$ N=2\mathbf{\nu}=2\cdot 1\ 000=2\ 000. $$

Відповідь: 1. 0,001. 2. 2000.

ТЕМА: Механіка. Основи динаміки. Другий і третій закон Ньютона.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням другого і третього законів Ньютона.

Дано:
\(m=2\cdot 10^6\ \text{кг}\)
\(F_1=500\ \text{кН}\)
\(F_2=600\ \text{кН}\)

Знайти:
\(a\ -\ ?\)

Якщо поїзд рухався рівномірно по горизонтальній поверхні, то його прискорення в першому випадку дорівнювало нулю. Отже й рівнодійна всіх сил, що діють на цей потяг, також дорівнювала нулю: $$ F_{\text{рівн}\ 0}=ma_0=0. $$

Отже в початковому стані сила, що тягне вагони, дорівнювала силам, що протидіють рухові потяга (силі тертя, силі опору повітря, тощо).

Коли тягова сила збільшилась, то рівнодійна всіх сил, що діяли на потяг перестала дорівнювати 0 – сили, що тягнуть вагони перевищали сили, що протидіють їх руху. $$ F_{\text{рівн}}=F_{\text{тяг}}-F_{\text{оп}}=ma. $$

Зважаючи на те, що в першому випадку тягові сили дорівнювали силам опору, можна обчислити рівнодійну після прискорення:

Тому можна обчислити прискорення:

Відповідь: 0,05.

ТЕМА: Механіка. Закони збереження в механіці.

Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі на використання законів збереження у випадку руху тіла по колу.

Дано:
\(l=50\ \text{см}\)

Знайти:
\(v_{min}\ -\ ?\)

У такій системі діятиме закон збереження механічної енергії. Механічна енергія – це сума кінетичної і потенціальної енергії тіла: $$ E_{\text{мех}}=E_{\text{пот}}+E_{\text{кін}}. $$

Кінетична енергія – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху: $$ E_{\text{кін}}=\frac{mv^2}{2}. $$

Потенціальна енергія – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою.

Для тіл, що перебувають у полі сили тяжіння, потенціальну енергію визначають за формулою $$ E_{\text{пот}}=mgh. $$

Якщо вважати, що в початковому положенні кулька перебуває на висоті 0 м від поверхні, то вся її механічна енергія складається лише з кінетичної енергії. Її швидкість у цей момент можна вважати саме тою мінімальною швидкістю, яку необхідно обчислити за умовою задачі:

Оскільки повна механічна енергія під час руху кульки не повинна змінюватися, то цієї кінетичної енергії має вистачити на те, щоби в найвищому положенні вона мала потенціальну енергію тіла, що перебуває на висоті \(2l\), і певну не нульову кінетичну енергію. Якщо кінетична енергія кульки в найвищій точці дорівнюватиме нулю, то вона зробить лише півоберта й упаде:

Тож за законом збереження енергії \begin{gather*} E_{\text{мех}}=E_{\text{мех}\ 0},\\[1pt] 2mgl+\frac{mv^2}{2}=\frac{mv^2_{min}}{2}. \end{gather*}

Кулька, що рухається по колу, має доцентрове прискорення. Зважаючи на те, що радіус кола дорівнює довжині нитки, у найвищій точці його можна обчислити за формулою: $$ a=\frac{v^2}{R}=\frac{v^2}{l}. $$

Тож за другим законом Ньютона \begin{gather*} ma=F_{\text{тяж}}+T_1,\\[1pt] m\frac{v^2}{l}=mg+T_1. \end{gather*}

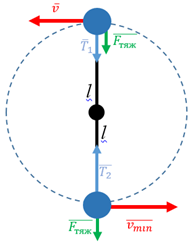
Рис. 1. Схематичне зображення дії сил на кульку під час руху

Щоби початкова швидкість була мінімальною, сила натягу нитки у верхній точці кола має дорівнювати нулю: \begin{gather*} m\frac{v^2}{l}=mg,\\[1pt] v^2=gl,\\[7pt] v=\sqrt{gl}. \end{gather*}

Тож можна підставити цей вираз для швидкості у верхній точці у вираз для закону збереження механічної енергії:

Відповідь: 5.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння теплового балансу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рівняння теплового балансу.

Дано:
\(t_{\text{льоду}}=0\ ^\circ\text{С}\)
\(\mathbf{\rho}_{\text{льоду}}=900\ \frac{\text{кг}}{\text{м}^3}\)
\(\mathbf{\rho}_{\text{монети}}=9,0\ \frac{\text{г}}{\text{см}^3}\)
\(c_{\text{монети}}=220\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)
\(\mathbf{\lambda} =330\ \text{кДж/кг}\)

Знайти:
\(t_{\text{монети}}\ -\ ?\)

Вважатимемо, що коли монета повністю занурена в лід, установлюється теплова рівновага. Тобто монета охолоджується від своєї початкової температури до 0 °C. Усю енергію від охолодження монети буде витрачено на танення льоду. Якщо монета занурилась у лід повністю, то об’єм льоду, що розтанув, дорівнює об’єму монети.

Маса тіла пов’язана з його об’ємом формулою $$ m=\mathbf{\rho}V, $$ де \(V\) – об’єм тіла, \(\mathbf{\rho}\) – густина тіла.

Теплоту, яку тіло втрачає під час охолодження, можна обчислити за формулою \begin{gather*} Q=cm\triangle t, \end{gather*} де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – маса, \(\triangle t\) – зміна температури під час охолодження.

Теплота, необхідна для танення льоду, може бути розрахована за формулою: $$ Q=\mathbf{\lambda}m, $$ де \(m\) – маса, \(\mathbf{\lambda}\) – питома теплота плавлення речовини.

Тоді можна записати рівняння теплового балансу: $$ c_{\text{монети}}m_{\text{монети}}\triangle t=\mathbf{\lambda}m_{\text{льоду}}. $$

Підставивши вираз для маси тіла й зважаючи на те, що різницю температур для монети можна обчислити за формулою:

Відповідь: 150.

ТЕМА: Електродинаміка. Закони постійного струму. Паралельне і послідовне з’єднання провідників.

Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного і послідовного з’єднання провідників.

Знайти:
\(\frac{U}{U_5}\ -\ ?\)

Спочатку потрібно позначити напругу джерела як \(U\) й розглянути підключення елементів в електричному колі. У коло послідовно підключено резистор 1 і групу резисторів 2–5. Група резисторів – це дві паралельно підключені пари послідовно з’єднаних резисторів.

Правила послідовного і паралельного підключення такі:

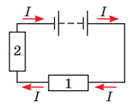
Рис. 1. Послідовне з’єднання провідників 1 і 2

\begin{gather*} U=U_1+U_2,\\[7pt] R=R_1+R_2,\\[7pt] I=I_1+I_2. \end{gather*}

Тому сила струму, яку вимірює амперметр – це сила струму на реостаті й на системі паралельно підключених провідників. За показниками на фотографії вона дорівнює 1,5 A.

Для паралельно підключених провідників правила такі:

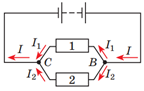
Рис. 2. Паралельне з’єднання провідників 1 і 2

\begin{gather*} U=U_1=U_2,\\[1pt] \frac 1R=\frac{1}{R_1}+\frac{1}{R_2},\\[1pt] I=I_1+I_2. \end{gather*}

Нехай \(I\) – сила струму, що проходить у колі, \(U\) – напруга в ньому, а \(R\) – опір кожного з однакових резисторів.

Оскільки резистор 1 і групу резисторів 2–5 підключено послідовно, можна записати: \begin{gather*} I_1=I_{2-5}=I,\\[7pt] U=U_1+U_{2-5},\\[7pt] R_{\text{заг}}=R+R_{2-5}. \end{gather*}

Напруга на групі резисторів 2–5 дорівнює напрузі на кожній парі резисторів, а сила струму на групі резисторів – це сума сил струму на кожній із пар: \begin{gather*} U_{2-5}=U_{2-3}=U_{4-5},\\[7pt] I_{2-5}=I_{2-3}+I_{4-5},\\[1pt] \frac{1}{R_{2-5}}=\frac{1}{R_{2-3}}+\frac{1}{R_{4-5}},\\[1pt] R_{2-5}=\frac{R_{2-3}R_{4-5}}{R_{2-3}+R_{4-5}}. \end{gather*}

Усередині кожної пари з’єднання послідовне, тому для цих резисторів також можна записати відношення для напруги й сили струму: \begin{gather*} I_{2-3}=I_{2}=I_3,\\[7pt] I_{4-5}=I_{4}=I_5,\\[7pt] U_{2-3}=U_2+U_{3},\\[7pt] U_{4-5}=U_4+U_{5},\\[7pt] R_{2-3}=R_{4-5}=R+R=2R. \end{gather*}

Напруга, сила струму й опору пов’язані між собою законом Ома: $$ I=\frac UR. $$

Можна обчислити загальний опір усіх резисторів:

Тоді можна записати співвідношення між силою струму в колі, напругою на обкладинках джерела й загальним опором резисторів у колі: $$ U=IR_{\text{заг}}=2IR. $$

Можна також записати аналогічне співвідношення для п’ятого резистора: $$ U_5=I_5R=I_{4-5}R. $$

Опір в обох парах резисторів дорівнює \(2R\) і напруга на них рівна, тому \begin{gather*} I_{2-3}=\frac{U_{2-3}}{2R}=\frac{U_{2-5}}{2R},\\[6pt] I_{4-5}=\frac{U_{4-5}}{2R}=\frac{U_{2-5}}{2R},\\[6pt] I_{2-3}=I_{4-5},\\[7pt] I_{2-5}=I_{2-3}+I_{4-5}=2I_{4-5}. \end{gather*}

Тож вираз для напруги п’ятого резистора теж спроститься: $$ U_5=I_5R=I_{4-5}R=\frac{I_{2-5}}{2}R=\frac I2 R. $$

Тоді $$ \frac{U}{U_5}=\frac{2IR}{\frac I2 R}=4. $$

Відповідь: 4.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.

У камері Вільсона частинки рухаються по дугах – елементах кола, отже камера перебуває в магнітному полі \(рис. 1\).

Рис. 1. Треки заряджених частинок у камері Вільсона

Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.

Доцентрове прискорення можна обчислити з виразу: $$ a_{\text{доц}}=\frac{v^2}{R}, $$ де \(v\) – швидкість частинка, а \(R\) – радіус треку.

За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца: $$ \overrightarrow{F_{\text{Лоренца}}}=Bvq\sin\mathbf{\alpha}, $$ де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і напрямком руху частинки.

Зважаючи на те, що частинки рухаються в полі по колу, то \(\mathbf{\alpha}=90^\circ\), а \(\sin\mathbf{\alpha}=1\), як це зображено на рисунку 2.

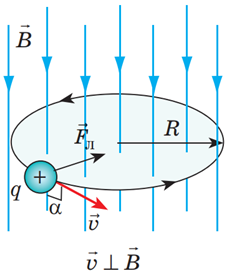
Рис. 2. Схема руху позитивно зарядженої частинки по колу

Тоді для випадку, описаного в задачі, можна записати: \begin{gather*} \overrightarrow{F_{\text{Лоренца}}}=m\overrightarrow{a_{\text{доц}}},\\[6pt] Bvq=m\frac{v^2}{R}. \end{gather*}

Вираз для кінетичної енергії тіла: $$ E_k=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, а \(v\) – швидкість його руху.

Тож можна виразити швидкість руху частинки з другого закону Ньютона для випадків до і після проходження крізь фольгу й обчислити кінетичні енергії для обох випадків: \begin{gather*} v_{\text{до}}=\frac{BR_{\text{до}}q}{m},\\[6pt] v_{\text{після}}=\frac{BR_{\text{після}}q}{m}. \end{gather*}

Співвідношення радіусів треків до і після проходження крізь фольгу таке: \begin{gather*} R_{\text{до}}=2R_{\text{після}},\\[6pt] v_{\text{після}}=\frac{BR_{\text{після}}q}{m},\\[6pt] v_{\text{до}}=\frac{2BR_{\text{після}}q}{m}. \end{gather*}

А кінетичні енергії матимуть вигляд:

Можна обчислити різницю кінетичних енергій до i після проходження крізь фольгу:

Тоді, знайшовши відношення цієї різниці до початкової кінетичної енергії, можна визначити, на скільки зменшилася кінетична енергія: $$ \frac{\triangle E_k}{E_{k\ \text{до}}}=\frac{3E_{k\ \text{після}}}{4E_{k\ \text{після}}}=0,75. $$

Ця різниця становитиме 75 %.

Відповідь: 75.

ТЕМА: Оптика. Лінза. Оптична сила лінзи.

Завдання скеровано на оцінювання вміння розв’язувати графічні задачі на зображення ходу світлових променів у системах із лінзами.

Оптична сила лінзи \(D\) пов’язана з фокусною відстанню лінзи \(F\) так: $$ D=\frac 1F. $$

Тобто $$ F=\frac 1D. $$

За формулою тонкої лінзи відстань \(d\) від об’єкта до лінзи, відстань \(f\) від лінзи до зображення і фокусна відстань пов’язані таким співвідношенням: $$ \frac 1F=\frac 1d+\frac 1f. $$

Уважатимемо, що світло рухається зліва направо. Оскільки зображення уявне, то і зображення, і предмет будуть розташовані зліва від лінзи. У такому разі відстань від предмета до лінзи у формулі буде додатною, бо напрямок переміщення від предмета до лінзи збігається із напрямком ходу променів. Відстань від лінзи до зображення у формулі тонкої лінзи буде від’ємною, адже переміщення від лінзи до зображення в цьому разі протилежно направлене до напрямку ходу променю.

Тоді можемо обчислити відстань від лінзи до зображення:

Відповідь: 20.