ЗНО онлайн 2018 року з фізики – додаткова сесія

ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Закон всесвітнього тяжіння.

Завдання скеровано на перевірку розуміння закону всесвітнього тяжіння і його застосування для описування реальних ситуацій.

Закон всесвітнього тяжіння – будь-які два тіла притягуються одне до одного із силою, яка прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними: $$ F=G\frac{m_1m_2}{r^2}, $$ де \(G\) – гравітаційна стала, \(m_1\) – маса першого тіла, \(m_2\) – маса другого тіла, \(r\) – відстань між ними.

Відстань між двома сусідніми цеглинами дорівнює \(0\), тож для них не можна використовувати закон всесвітнього тяжіння.

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Додавання сил.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.

За другим законом Ньютона рівнодійна всіх сил, що діють на тіло, пов’язана з його прискоренням формулою $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Тож напрямок прискорення збігається з напрямком рівнодійної всіх сил.

Рівнодійну всіх зображених на рисунку сил можна визначити за методом паралелограма (методом графічного додавання векторів). Додавання трьох сил можна виконати покроково: спочатку додати сили \(\overrightarrow{F_2}\) та \(\overrightarrow{F_3}\) (рис. 1, а), а потім результат цієї дії додати до сили \(\overrightarrow{F_1}\) (рис. 1, б)

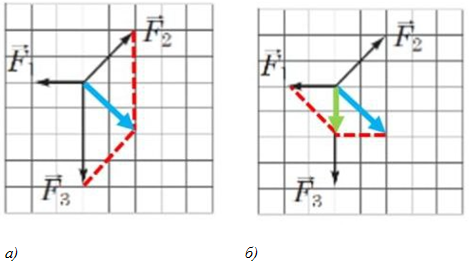
Рис. 1. Графічний спосіб визначення рівнодійної

Рівнодійна (позначена зеленим кольором на рис. 1, б), а отже й прискорення тіла спрямовані вниз.

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку вміння використовувати закон збереження імпульсу.

Абсолютно непружне зіткнення – це зіткнення, після якого тіла рухаються як одне ціле.

Тож зчеплення тепловоза з вагоном можна вважати абсолютно пружним.

Для визначення швидкості поїзда після зчеплення необхідно скористатися законом збереження імпульсу: $$ \overrightarrow{p_{M\text{до}}}+\overrightarrow{p_{m\text{до}}}=\overrightarrow{p_{\text{після}}}. $$

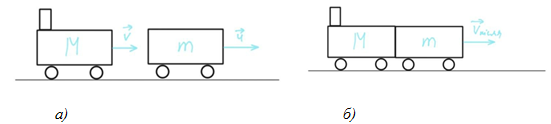
Рис. 1. Положення вагонів до зіткнення (а) та після зіткнення (б)

Оскільки вагон і тепловоз рухаються в одному напрямку , то закон збереження імпульсу можна спроєктувати на напрямок їхнього руху: $$ p_{M\text{до}}+p_{m\text{до}}=p_{\text{після}}. $$

Імпульси вагонів можна обчислити за формулою $$ \overrightarrow{p}=m\overrightarrow{v}, $$ де \(m\) – це маса тіла, а \(\overrightarrow{v}\) – його швидкість.

Тоді

Підставивши проєкції відповідних імпульсів у закон збереження, отримаємо:

Відповідь: Г.

ТЕМА: Механіка. Потенціальна енергія. Сила пружності.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формул для обчислення потенціальної енергії тіл.

Потенціальну енергію пружного тіла визначають за формулою $$ U=\frac{kx^2}{2}, $$ де \(k\) – жорсткість тіла, \(x\) – його абсолютне видовження.

Саме цю енергію пружина передає кульці під час розтискання. Отримана від пружини енергія перейде в її кінетичну та потенціальну енергію. У найвищій точці свого польоту кулька має найбільшу потенціальну енергію.

Для тіл, що перебувають у полі сили тяжіння (як тіла із завдання), потенціальну енергію визначають за формулою $$ U_{\text{п}}=mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.

Тоді для першого досліду можна записати рівність $$ \frac{kx^2_1}{2}=mgh_1. $$

Відповідно $$ k=\frac{2mgh_1}{x^2_1}. $$

Для другого досліду також виконувана рівність $$ \frac{kx^2_2}{2}=mgh_2. $$

У цю рівність можна підставити вираз для \(k\) й визначити висоту \(h_2\):

Усі відстані в умові необхідно виразити в метрах. Тоді

Відповідь: B.

ТЕМА: Сполучені посудини.

Завдання скеровано на перевірку вміння розв’язувати задачі зі сполученими посудинами.

У сполучених посудинах у кожній трубці рівень рідин установлюється так, що гідростатичний тиск стовпчика однакової рідини у них рівний.

Гідростатичний тиск \(p\) визначають за формулою $$ p=\mathbf{\rho}gh, $$ де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Якщо рідини в трубках однорідні, то тиск на однаковій висоті в усіх трубках буде однаковим. Але в лівій трубці посудини рівень олії вищий, ніж рівень води в правій трубці, адже олія має меншу густину. Щоби створити такий самий гідростатичний тиск, як і в правій трубці, висота стовпчика рідини має бути більшою.

Порівняймо точки, позначені на рисунку.

У точці В тиск дорівнює атмосферному \((p_a)\), а в точці А до атмосферного тиску додається тиск стовпчика гасу над рівнем цієї точки. Отже \(p_A\gt p_B\).

Точка С в правій трубці на тому ж рівні, що межа розділу двох рідин у лівій трубці, тому тиск у ній дорівнює тиску всього стовпчика олії. Висота всього стовпчика олії більша за висоту стовпчика над точкою А, тому \(p_C\gt p_A\).

Точка D перебуває найглибше з усіх точок у воді, тому тиск на неї найбільший.

Відповідь: A.

ТЕМА: Кількість речовини.

Завдання скеровано на перевірку розуміння поняття кількості речовини.

Кількість речовини можна визначити за формулою $$ v=\frac{N}{N_A}, $$ де \(N\) – кількість молекул, \(N_A\) – число Авогадро.

Нехай кількість речовини озону становить \(v\). Кожна молекула озону утворена трьома атомами Оксигену. Тоді для утворення нових молекул доступно \(3v\) атомів. Кожна молекула кисню утворена двома атомами Оксигену, тож всього їх можна буде утворити \(3v:2=1,5v\).

Відповідь: B.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за підвищення температури та звужуються за її зниження).

Динамометр – це прилад для вимірювання сили. Зазвичай складники динамометра – пружина та шкала. Коли на кінець пружини діє сила, то, за законом Гука, пружина розтягується.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплена стрілка. Тому, коли кришка камери піднімається чи опускається, пружина деформується і стрілка починає рухатися по шкалі.

Електрометр – це прилад для виявлення та вимірювання заряду. Його складники – металева куля, стержень і стрілки. Під дією електричного поля в стержні, стрілці й кулі відбувається перерозподіл зарядів. Оскільки вони з’єднані, то заряджаються однаково. Однойменно заряджені стрілка та стержень відштовхуються, тому рухома стрілка відхиляється.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки.

Завдання скеровано на розуміння суті адіабатного процесу.

Оскільки зміна внутрішньої енергії відбувається без передавання теплоти ззовні, то описаний процес – адіабатний.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.

Завдання скеровано на оцінювання розуміння понять динамічної рівноваги й відносної та абсолютної вологості.

Абсолютна вологість – фізична величина, якою характеризують уміст водяної пари в повітрі. Вона чисельно дорівнює масі водяної пари в повітрі об’ємом \(1\ \text{м}^3\).

Відносна вологість – фізична величина, яка показує, наскільки водяна пара близька до насичення. Вона дорівнює відношенню абсолютної вологості до густини насиченої водяної пари за певної температури або відношенню парціального тиску водяної пари за певної температури до тиску насиченої пари за тої самої температури (у частках від одиниці або у відсотках).

Tочка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.

Питома теплоємність – кількість теплоти, яку необхідно надати одиниці маси речовини й нагріти її на \(1\ ^\circ\text{С}\).

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу.

Завдання скеровано на перевірку вміння аналізувати графічні залежності температури тіла від кількості наданої йому теплоти.

Кількість наданої теплоти, температура тіла та його питома теплоємність пов’язані виразом $$ Q=cm\Delta T=cm(T-T_0), $$ де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – маса, \(\Delta T\) – зміна температури під час охолодження, \(T_0\) – початкова температура, \(T\) – температура тіла.

Графік у завданні – це графік залежності абсолютної температури тіла \(T\) від часу його нагрівання \(t\). Оскільки щосекунди тіло отримує однакову кількість теплоти \(Q\), залежність абсолютної температури \(T\) від кількості теплоти \(Q\) має схожий вигляд. Тому надалі достатньо аналізувати залежність \(T(Q)\).

Для цього необхідно змінити вигляд залежності:

Залежність має вигляд лінійної функції \(y=kx+b\), де \(b\) відповідає за перетин із віссю \(oy\), а \(k\) – кутовий коефіцієнт, що впливає на нахил прямої: $$ b=T_0,\ \ k=\frac{1}{cm}. $$

Оскільки маси всіх трьох тіл однакові, то на нахил прямої, що відповідає лінійній функції, впливає лише питома теплоємність.

Що більший кутовий коефіцієнт, то крутішою є пряма, а кутовий коефіцієнт є тим більшим, що меншою є питома теплоємність.

Тож найпологіша пряма (для тіла 1) має найбільшу питому теплоємність, а найкрутіша (для тіла 2) – найменшу.

Відповідь: Г.

ТЕМА: Основи електростатики. Закон Кулона.

Завдання скеровано на оцінювання розуміння взаємодії між електричними зарядами.

У металевому тілі багато вільних електронів, що рухаються під дією зовнішнього електричного поля. Негативно заряджені електрони в металевому тілі рухатимуться до позитивного заряду, тож ділянка 1 матиме надлишок електронів, а ділянка 2 – їхню нестачу.

Тобто ділянка 2 буде заряджена позитивно, а 1 – негативно.

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики.

Завдання скероване на оцінку розуміння принципу роботи джерела струму.

Джерела електричного струму повинні виштовхувати електрони в електричне коло. Вони мають позитивно й негативно заряджені полюси. Електрони рухаються він негативного полюса до позитивного по провідниках у колі. Проте відстань між двома полюсами джерела набагато менша за довжину будь-якого кола. Частинки, що притягуються, завжди рухаються найкоротшим шляхом. Тож чому електрони взагалі покидають джерело струму й опиняються в колі, а не просто рухаються в межах джерела?

В усіх джерелах діють сторонні сили, що змушують електрони рухатись до негативно зарядженого полюса. Сторонні сили протидіють кулонівським у джерелі, які прагнуть перемістити електрони до позитивно зарядженого полюса. Схематично дію сторонніх і кулонівських сил у джерелі струму зображено на рисунку 1. Синім кольором позначено кулонівські сили, а червоним – сторонні.

Тож джерело струму не може працювати без дії сторонніх сил усередині.

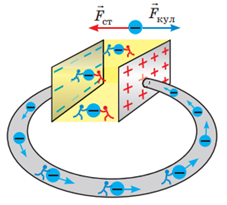
Рис. 1. Схематичне зображення дій сторонніх і кулонівських сил у джерелі струму

Відповідь: Б.

ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку розуміння поняття роботи сили.

Роботу сили можна обчислити за формулою: $$ A=Fs\cos\mathbf{\alpha}, $$ де \(F\) – сила (H), \(s\) – переміщення (м), \(\mathbf{\alpha}\) – кут між напрямком переміщення і сили.

Поле не виконує роботу над зарядженою частинкою, якщо \(\cos\mathbf{\alpha}=0\), тобто якщо сила, яка діє на частинку в полі, завжди перпендикулярна до її переміщення.

Відповідно на електрично заряджену частинку діє лише сила Лоренца в сталому магнітному полі.

Відповідь: Г.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку розуміння поняття термоелектронної емісії.

Нитка розжарення нагріває катод, у результаті чого деякі його електрони отримують кінетичну енергію, більшу за роботу виходу матеріалу, і покидають катод.

Якщо катод підключений до негативного полюсу джерела, а анод до позитивного, то електрони, що утворилися внаслідок термоелектронної емісії, починають рухатися до анода, тобто через діод тече струм. Якщо полюси джерела підключити навпаки, то поле на катоді затримуватиме електрони.

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку розуміння залежності магнітного потоку від зовнішніх чинників.

Магнітний потік \(\mathbf{\Phi}\) – це фізична величина, яка дорівнює добуткові магнітної індукції \(B\) на площу \(S\) поверхні та на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю до поверхні: $$ \mathbf{\Phi}=BS\cos\mathbf{\alpha}, $$ де \(B\) магнітна індукція, \(S\) – площа поверхні, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції та нормаллю до поверхні.

Тож магнітний потік, що пронизує плоске дротяне кільце, зміниться, якщо змінити його площу (зім’яти його), змінити напруженість магнітного поля, що проходить крізь кільце (помістити всередину кільця залізне осердя) чи якщо змінити кут між вектором магнітної індукції та нормаллю до поверхні (повернути кільце навколо осі, що проходить у його площині).

Відповідь: B.

ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку розуміння природи сили Лоренца.

У магнітному полі на заряджену частинку діє сила Лоренца, яку можна розрахувати за формулою $$ \overrightarrow{F_{\text{Лоренца}}}=Bvq\sin\mathbf{\alpha}, $$ де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції та напрямком руху частинки.

Частинка продовжуватиме свій рух по прямій без змін, якщо \(\sin\mathbf{\alpha}=0\), тобто магнітна індукція та напрямок руху частинки мають лежати на паралельних прямих.

Відповідь: Б.

ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку розуміння зв’язку між частотою хвилі, її довжиною та швидкістю поширення.

Частота хвилі, її довжина та швидкість поширення пов’язані формулою $$ v=\mathbf{\nu}\mathbf{\lambda}, $$ де \(v\) – швидкість поширення хвилі, \(\mathbf{\nu}\) – частота, \(\mathbf{\lambda}\) – довжина хвилі.

Частота не змінюється під час переходу з одного середовища в інше.

За умовою завдання відомо, що швидкість поширення хвилі під час переходу збільшилася. Якщо частота не змінюється, то лише зміна довжини хвилі може привести до зміни швидкості поширення. Якщо швидкість збільшилася, то й довжина хвилі також збільшилася.

Відповідь: B.

ТЕМА: Механічні коливання та хвилі. Частота й період коливань. Вимушені коливання та явище резонансу.

Завдання скеровано на перевірку розуміння поняття резонансу.

Резонанс – це явище різкого збільшення амплітуди, яке виникає, якщо частота зовнішньої сили, що періодично змінюється, збігається з власною частотою коливань системи.

Відповідь: A.

ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.

Коливальний контур – це фізичний пристрій, який складено з послідовно з’єднаних конденсатора й котушки індуктивності (рис. 1).

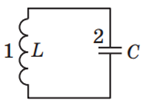
Рис. 1. Електрична схема коливального контуру: 1 – котушка індуктивності, 2 – конденсатор

В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Цей процес описують за допомогою формули $$ W_{\text{конденсатора}}=\frac{CU^2}{2}, $$ де \(U\) – напруга на обкладинках конденсатора, а \(C\) – його ємність.

Під час коливань у контурі енергія повністю зарядженого конденсатора перетікатиме в енергію котушки, яку можна визначити за формулою $$ W_{\text{котушки}}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.

У контурі електрони, що накопичилися на одній з обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм у колі. У результаті цього конденсатор почне розряджатися, напруга на його обкладинках зменшується, а отже зменшуватиметься і його енергія.

У котушці ж сила струму поступово збільшуватиметься, а разом із нею збільшуватиметься й енергія магнітного поля, яке вона створює. Коли конденсатор розрядиться повністю, струм у котушці стане максимальним.

Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається, а струм у котушці поступово зменшується.

Унаслідок цього процесу заряд з однієї обкладинки конденсатора опиниться на іншій обкладинці. Тож тепер конденсатор заряджений протилежно до початкового стану, і напруга на ньому за модулем дорівнює початковій напрузі, але має протилежний знак.

Після цього струм почне текти в протилежному напрямку. Одне повне коливання закінчиться тоді, коли заряд повністю повернеться на першу обкладинку.

Тож за одне коливання потенціальна енергія конденсатора двічі досягає максимуму (коли весь заряд опиняється на одній з обкладинок) і двічі досягає \(0\) (коли струм у котушці максимальний).

Відповідь: Г.

ТЕМА: Оптика. Лінза. Плоске дзеркало.

Завдання скеровано на перевірку розуміння принципів роботи основних оптичних елементів.

Плоске дзеркало може створити зображення тіла, що має такий самий розмір, як і сам об’єкт.

Перископ, що складений із кількох дзеркал і дає змогу перенаправити промені від об’єкта до спостерігача, так само може створити лише зображення такого ж розміру, як і об’єкт.

Розсіювальна лінза завжди створює зменшене уявне зображення, а збиральна лінза може створити уявне збільшене зображення, якщо відстань від лінзи до тіла менша за її фокусну відстань.

Відповідь: Г.

ТЕМА: Оптика. Квантова фізика. Світлові кванти.

Завдання скеровано на перевірку розуміння механізму фотоефекту.

Енергію, отриману від фотона, електрон витрачає на те, щоби вирватися з поверхні металу (робота виходу \(A_{\text{вих}}\)) і на його рух після цього (кінетична енергія \(E_{\text{кін}}\): $$ E=A_{\text{вих}}+E_{\text{кін}}. $$

Якщо фотони з енергією \(E=1,5\ \text{еВ}\) зумовлюють вилітання електронів із поверхні, то $$ E=1,5\ \text{еВ}\gt A_{\text{вих}}. $$

З тих самих міркувань, якщо енергія фотона \(E=1\ \text{еВ}\) і він не зумовлює вилітання електрона з поверхні, то \(E=1\ \text{еВ}\gt A_{\text{вих}}\).

Відповідь: Б.

ТЕМА: Квантова фізика. Атом та атомне ядро.

Завдання скеровано на оцінку розуміння досліду Резерфорда.

Під час досліду Резерфорд бомбардував позитивно зарядженими альфа-частинками тонку фольгу золота, лише кілька атомів завтовшки. Деякі альфа-частинки відбивалися від фольги майже в протилежному напрямку, що було можливо лише якщо ця частинка «відбивається» від якоїсь важкої частинки в атомі – ядра. Позитивно заряджене ядро та позитивно заряджена альфа-частинка відштовхуються завдяки електричній взаємодії (за законом Кулона).

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.

Завдання скерованo на перевірку розуміння природи спектрів поглинання і випромінювання.

Модель атома Бора є вдосконаленням планетарної моделі. Один із головних недоліків планетарної моделі такий: якщо описувати рух електронів навколо ядра законами класичної механіки, то електрони б постійно наближались до ядра і з часом впали б на нього. Такий атом не може існувати.

Тому Бор сформулював постулати:

1) атомна система може перебувати тільки в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії. Перебуваючи в стаціонарному стані, атом не випромінює енергію;

2) під час переходу з одного стаціонарного енергетичного стану (з енергією \(E_k\)) в інший (з енергією \(E_n\)) атом випромінює або поглинає квант електромагнітної енергії: $$ h\mathrm{v}=|E_k-E_n|. $$

У кванта електромагнітної хвилі специфічнa частотa, для видимого випромінювання це означає, що випромінений квант на спектрах випромінювання має вигляд вузької кольорової смужки. У спектрі поглинання поглинутий квант має вигляд вузької темної смужки.

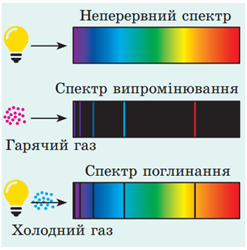
Рис. 1. Вигляд лінійчастих спектрів поглинання і випромінювання

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.

Завдання скеровано на перевірку розуміння зв’язку між силою, прискоренням і швидкістю руху тіла.

А Важок математичного маятника здійснює коливальний рух, під час якого швидкість тіла змінюється від 0 в найвищій точці його траєкторії до максимального значення в найнижчій. Окрім того напрямок руху важка змінюється двічі за коливання, тож і швидкість також змінює свій напрямок постійно.

Б Швидкість літака, що гальмує на посадковій смузі, зменшується за модулем, але її напрямок не змінюється.

В Швидкість, автомобіля, що рухається по прямій дорозі рівномірно, не змінюється.

Г Горіх, що падає на Землю з дерева, рухається лише під дією її сили тяжіння, тобто з прискоренням вільного падіння. Модуль швидкості тіла в такому разі збільшується, а напрямок не змінюється.

Д Стрілка годинника рухається по колу з однаковою лінійною швидкістю, проте будь-який рух по колу супроводжуваний доцентровим прискоренням, що змушує напрямок миттєвої швидкості безперервно змінюватися.

Відповідь: 1Б, 2Г, 3Д, 4А.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна та відносна вологість. Точка роси.

Завдання скерованo на перевірку розуміння понять точки роси, випаровування, кристалізації та адіабатного процесу.

А Роса почне формуватися, коли повітря сягне точки роси. Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.

Б Стискання повітря в насосі відбувається настільки швидко, що воно не встигає обмінятись енергією з довкіллям. У такому разі робота, виконана тілом, переходить у його внутрішню енергію.

В Замерзання водоймищ восени – це приклад кристалізації рідини.

Г Висихання білизни після прання – це приклад випаровування рідини.

Д Іній – це тонкий шар льоду на поверхнях. Він утворюється завдяки тому, що водяна пара в повітрі кристалізується.

Відповідь: 1Г, 2Б, 3А, 4Д.

ТЕМА: Одиниці фізичних величин.

Завдання скеровано на перевірку вміння записувати одиниці фізичних величин через основні одиниці СІ.

1 Тесла (магнітна індукція)

Варто вибрати формулу, з якої можна виразити магнітну індукцію через величини, одиниці яких входять в СІ, або можуть бути легко вираженi через них. Для магнітної індукції можна використати вираз для сили Ампера: $$ F_A=BIl\rightarrow B=\frac{F_A}{Il}, $$ де \(I\) – сила струму в провіднику (А), \(l\) – довжина провідника (м).

Тоді можна записати рівність (1), використовуючи одиниці фізичних величин:

2 Генрі (індуктивність): $$ W=\frac12 LI^2\rightarrow L=\frac{2W}{I^2}, $$ де \(W\) – енергія магнітного поля котушки (Дж), \(I\) – сила струму (А). $$ L=\frac{2W}{I^2}\rightarrow 1\ \text{Гн}=\frac{\text{Дж}}{\text{А}^2}= \frac{\text{кг}\cdot\text{м}^2}{\text{с}^2}\cdot\frac{1}{\text{А}^2}. $$

3 Ньютон (сила): $$ F=mg, $$ де \(m\) – маса (кг), \(g\) – прискорення вільного падіння \(\left(\frac{\text{м}}{\text{с}^2}\right)\): $$ F=mg\rightarrow 1\ \text{Н}=\text{кг}\cdot\frac{\text{м}}{\text{с}^2}. $$

4 Джоуль (робота): $$ A=Fs\cos\mathbf{\alpha}, $$ де \(F\) – сила (Н), \(s\) – переміщення (м), \(\mathbf{\alpha}\) – кут між напрямком переміщення і сили: $$ A=Fs\cos\mathbf{\alpha}\rightarrow 1\ \text{Дж}=\text{Н}\cdot\text{м}=\text{м}\cdot \frac{\text{кг}\cdot\text{м}}{\text{с}^2}. $$

Відповідь: 1В, 2А, 3Д, 4Б.

ТЕМА: Оптика. Інтерференція світла. Дисперсія світла. Поляризація світла.

Завдання скеровано на перевірку розуміння застосовності оптичних явищ у техніці.

А Рідкі кристали в дисплеї пропускають лише світло певної поляризації. Під час проходження струму, рідкий кристал змінює свою форму / положення, у результаті чого змінюється і поляризація, яку він пропускає. Саме так формується зображення.

Б Для виготовлення дзеркал скло високої якості вкривають тонким шаром металу, що відбиває світло.

В Для того, щоби зменшити вплив відбивання світла на границях лінз, на їхні поверхні наносять тонкі плівки. У результаті інтерференції для певних довжин хвиль відбиті промені накладаються та гасять одне одного.

Г Лазер є основним джерелом енергії, яка руйнує шар металу під час різання. Усю ця енергію поглинає метал, унаслідок чого підвищується температура в опроміненій ділянці, що й приводить до руйнування.

Д Світловий промінь залишається всередині довгого оптичного волокна завдяки тому, що він падає на стінки волокна під кутом повного внутрішнього відбивання (або більшим кутом), тож замість того, щоби заломлюватися на межі скла й повітря, промінь відбивається і продовжує свій рух усередині.

Відповідь: 1А, 2В, 3Г, 4Д.

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на рівноприскорений рух.

Дано:
\(t=5\ \text{с}\)
\(v_0=0\ \frac{\text{м}}{\text{с}}\)
\(v=10\ \frac{\text{м}}{\text{с}}\)
\(t_1=4\ \text{с}\)

1. Знайти:
\(a\ \left(\frac{\text{м}}{\text{с}^2}\right)\ -\ ?\)

Швидкість за рівноприскореного руху можна визначити за формулою $$ v=v_0+at, $$ де \(v_0\) – початкова швидкість, \(a\) – прискорення, \(t\) – час руху тіла.

Оскільки тіло рухається зі стану спокою, то початкова швидкість тіла дорівнює нулю, тоді $$ v=at. $$

Тож з формули можна виразити прискорення: \begin{gather*} a=\frac vt=\frac{10\ \frac{\text{м}}{\text{с}}}{5\ \text{с}}=2\ \frac{\text{м}}{\text{с}^2} \end{gather*}

2. Знайти:
\(l\ (\text{м})\ -\ ?\)

Шлях, пройденим тілом, під час рівноприскореного руху можна визначити за формулою $$ l=v_0t+\frac{at^2}{2}, $$ де \(v_0\) – початкова швидкість тіла, \(a\) – прискорення тіла, \(t\) – час руху тіла.

Початкова швидкість тіла дорівнює нулю, тож шлях, який тіло пройшло за \(4\ \text{с}\), можна обчислити за формулою \begin{gather*} l=\frac{at^2}{2}=2\ \frac{\text{м}}{\text{с}^2}\cdot\frac{(4\ \text{с})^2}{2}=16\ \text{м}. \end{gather*}

Відповідь: 1. 2. 2. 16.

ТЕМА: Теплота згоряння палива. Рівняння теплового балансу палива. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з рівняннями теплового балансу.

Дано:
\(m=3\ \text{кг}\)
\(t_1=40\ ^\circ\text{С}\)
\(c_{\text{води}}=4200\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)
\(r=2300\ \frac{\text{кДж}}{\text{кг}}\)
\(q=45\ \frac{\text{МДж}}{\text{кг}}\)
\(\mathbf{\rho}=0,8\ \frac{\text{кг}}{\text{м}^3}\)
\(t_2=100\ ^\circ\text{С}\)

1. Знайти:
\(V\ (\text{м}^3)\ -\ ?\)

Необхідну для нагрівання води до температури кипіння \((100\ ^\circ\text{С})\) кількість енергії можна визначити за формулою \begin{gather*} Q_{\text{нагр}}=cm(t_2-t_1), \end{gather*} де \(c\) – питома теплоємність тіла, \(m\) – маса тіла, \(t_1\) – початкова температура тіла, \(t_2\) – кінцева температура тіла.

Енергію, що виділиться під час спалювання газу, можна визначити за формулою $$ Q_{\text{спал}}=qm, $$ де \(q\) – питома теплота згоряння палива, \(m\) – маса тіла.

Маса палива пов’язана з його густиною та об’ємом формулою $$ m_{\text{пал}}=\mathbf{\rho}_{\text{пал}}V_{\text{пал}}, $$ де \(\mathbf{\rho}\) – густина палива, \(V\) – об’єм палива.

Тоді рівняння теплового балансу таке:

2. Знайти:
\(Q\ (\text{кДж})\ -\ ?\)

Для того, щоби випарувати воду, її необхідно нагріти до температури кипіння \((100\ ^\circ\text{С})\). Необхідну для нагрівання кількість енергії можна визначити за формулою \begin{gather*} Q_{\text{нагр}}=cm(t_2-t_1), \end{gather*} де \(c\) – питома теплоємність тіла, \(m\) – маса тіла, \(t_1\) – початкова температура тіла, \(t_2\) – кінцева температура тіла.

Енергію, необхідну для випаровування води, можна визначити за формулою $$ Q_{\text{вип}}=rm, $$ де \(r\) – питома теплота пароутворення, \(m\) – маса тіла.

Тоді можна обчислити загальну необхідну кількість теплоти:

Відповідь: 1. 0,021. 2. 7656.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу. Робота. Потужність. Коефіцієнт корисної дії (ККД).

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі, пов’язані з електричною потужністю і рівнянням теплового балансу.

Дано:
\(R=20\ \text{Ом}\)
\(U=200\ \text{В}\)
\(m=1\ \text{кг}\)
\(t_1=20\ ^\circ\text{С}\)
\(t_2=100\ ^\circ\text{С}\)
\(t=200\ \text{с}\)
\(c=4200\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)

1. Знайти:
\(A\ (\text{кДж})\ -\ ?\)

Потужність пов’язана з роботою формулою $$ P=\frac At, $$ де \(A\) – виконувана робота, а \(t\) – час виконання роботи.

Потужність електричного нагрівача можна визначити за формулою $$ P=UI=\frac{U^2}{R}, $$ де \(U\) – напруга, \(I\) – сила струму.

Тож

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД нагрівача визначають як відношення корисної роботи, виконаної ним, до повної роботи: \begin{gather*} \text{ККД}=\frac{Q}{A_\text{пов}}\cdot 100\ \text{%}, \end{gather*} де \(Q\) – це енергія, що необхідна для нагрівання води.

Необхідну для нагрівання води кількість енергії можна визначити за формулою $$ Q=cm(t_2-t_1), $$ де \(c\) – питома теплоємність тіла, \(m\) – маса тіла, \(t_1\) – початкова температура тіла, \(t_2\) – кінцева температура тіла.

Повна робота – це робота струму в електричному нагрівачі, тож

Відповідь: 1. 400. 2. 84.

ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули Томсона.

Дано:
\(L=10\ \text{мГн}\)
\(C=40\ \text{мФ}\)
\(\mathbf{\pi}=3,14\)

1. Знайти:
\(\mathbf{\omega}\ -\ ?\)

Знаючи ємність конденсатора й індуктивність котушки коливального контуру можна визначити період коливань T, які виникають під час його роботи: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, \(C\) – електрємність конденсатора.

Циклічна частота пов’язана з періодом коливань формулою $$ \mathbf{\omega}=\frac{2\mathbf{\pi}}{T}. $$

Тоді

2. Знайти:
\(t (\text{мс})\ -\ ?\)

Енергію конденсатора в коливальному контурі можна визначити за формулою $$ W_{\text{кон}}=\frac{CU^2}{2}, $$ де \(U\) – напруга, а \(C\) – електроємність.

Енергію котушки обчислюють за формулою \begin{gather*} W_{\text{кот}}=\frac{LI^2}{2}, \end{gather*} де \(L\) – індуктивність, \(I\) – сила струму.

Енергія в коливальному контурі змінюється періодично. За один період у коливальному контурі заряд з одної обкладинки конденсатора протікає через котушку на іншу обкладинку, а потім назад. Тож за один період сила струму в котушці (а отже й енергія) дорівнює нулю двічі: на початку періоду та в момент \(T/2\). Нульова енергія на котушці відповідає максимальній енергії на конденсаторі.

Тоді в момент \(T/4\) енергія на котушці буде максимальною, а на конденсаторі дорівнюватиме нулю.

Перший раз енергія котушки й конденсатора зрівняється між моментами максимуму енергії конденсатора \((t=0)\) і котушки \((t=T/4)\), тобто в момент \(t=T/8\).

Цей час можна обчислити:

Відповідь: 1. 50. 2. 16.

ТЕМА: Механіка. Основи динаміки. Умови рівноваги.

Завдання скерованo на перевірку вміння розв’язувати задачі з використанням умов рівноваги.

Дано:
\(l=40\ \text{см}\)
\(F_A=4\ \text{Н}\)
\(F_B=1\ \text{Н}\)

Знайти:
\(A\ (\text{Дж})\ -\ ?\)

Рис. 1. Умова задачі

На рисунку зображено важіль. Умова рівноваги для важеля – це рівність моментів сил: $$ M_A=M_B, $$ де \(M_A\) і \(M_B\) – відповідні моменти сил.

Момент сил можна визначити за формулою $$ M=Fd, $$ де \(F\) – сила, що діє на плече, \(d\) – плече сили.

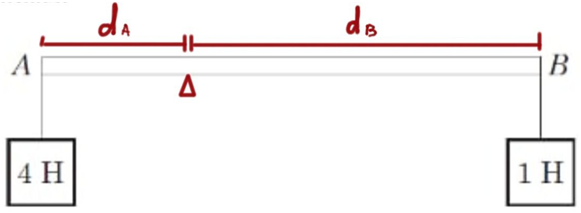
Рис. 2. Визначення плеча сили

Нехай плече сили, що прикладена в точці \(A-d_A=x\ (\text{м})\), а плече сили дорівнює \(d_B\). Оскільки довжина всього стержня дорівнює \(40\ \text{см}=0,4\ \text{м}\), то \(d_A+d_B=0,4\ \text{м}\), тож \(d_B=0,4-x\ (\text{м})\).

Тоді умову рівності моментів можна записати так:

Відповідь: 8.

ТЕМА: Динаміка рідин і газів. Потужність.

Завдання скеровано на перевірку розуміння поняття потужності та динаміки потоку рідини в трубі.

Дано:
\(V=0,2\ \text{м}^3\)
\(A=26\ \text{кДж}\)
\(\mathbf{\rho}_{\text{якір}}=7500\ \frac{\text{кг}}{\text{м}^3}\)
\(\mathbf{\rho}_{\text{води}}=1000\ \frac{\text{кг}}{\text{м}^3}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

Знайти:
\(l\ (\text{м})\ -\ ?\)

Роботу сили можна визначити за формулою $$A=Fs\cos\mathbf{\alpha},$$ де \(F\) – сила, \(s\) – переміщення, спричинене силою, \(\mathbf{\alpha}\) – кут між напрямком сили й переміщення.

На якір у воді діє сила тяжіння, сила Архімеда й зовнішня сила, що піднімає якір (рис. 1).

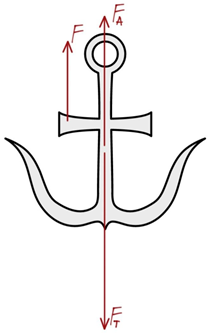
Рис. 1. Сили, що діють на якір

Формула, якою описують другий закон термодинаміки, така: \begin{gather*} \overrightarrow{F_\text{рівн}}=\overrightarrow{F}+\overrightarrow{F_T}+\overrightarrow{F_A}. \end{gather*}

Оскільки якір піднімають повільно, можна вважати, що прискорення дорівнює нулю, тоді в проєкції на вісь OY другий закон Ньютона можна записати так: \begin{gather*} 0=F-F_T+F_A;\\[7pt] F=F_T-F_A. \end{gather*}

Силу тяжіння визначають за формулою \begin{gather*} F_T=mg, \end{gather*} а силу Архімеда – за формулою $$F_A=\mathbf{\rho}_{\text{води}}gV.$$

Маса тіла, його густина й об’єм пов’язані формулою \begin{gather*} m=\mathbf{\rho}_{\text{якір}}V. \end{gather*}

Тож

Тоді, зважаючи на те, що напрямок сили та переміщення однакові,

\begin{gather*} A=Fl;\\[6pt] l=\frac AF=\frac{26\ \text{кДж}}{13000\ \text{Н}}=\frac{26000\ \text{Дж}}{13000\ \text{Н}}=2\ \text{м}. \end{gather*}

Відповідь: 2.

ТЕМА: Молекулярна фізика та термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння стану ідеального газу.

Дано:
\(T=7\ ^{\circ}\text{С}\)
\(p=166\ \text{кПа}\)
\(V=70\ \text{л}\)
\(R=8,3\ \frac{\text{Дж}}{\text{моль}\ \cdot\ \text{К}}\)

Знайти:
\(\mathbf{\nu}\ (\text{моль})\ -\ ?\)

Рівняння стану ідеального газу таке: $$ pV=\mathbf{\nu}RT, $$ де \(p\) – тиск газу, \(V\) – об’єм газу, \(T\) – температура газу, \(\mathbf{\nu}\) – кількість речовини, \(R\) – універсальна газова стала.

Тоді, після переведення всіх фізичних величин в одиниці СІ,

Відповідь: 5.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку розуміння впливу зовнішніх чинників на електроємність конденсатора.

Знайти:
\(\frac{S_2}{S_1}\ -\ ?\)

Електроємність конденсатора залежить від його геометричних характеристик: $$ C=\frac{\mathbf{\varepsilon}\mathbf{\varepsilon}_0S}{d}, $$ де \(\mathbf{\varepsilon}\) – діелектрична проникність діелектрика між обкладинками, \(\mathbf{\varepsilon}_0\) – електрична стала, \(S\) – площа обкладинок, \(d\) – відстань між обкладинками.

Під час повороту обкладинок конденсатора змінюється площа їхнього перекриття. Нехай довжина пластини становить \(5\) клітинок, а ширина – \(3\) клітинки. Тоді можна обчислити початкову площу перекриття в умовних одиницях: $$ S_1=3\cdot 5=15\ (\text{у. о.}). $$

Після повороту область перекриття перетворилася на квадрат зі стороною 3 клітинки, площа якої дорівнює:

Відповідь: 0,6.

ТЕМА: Оптика. Закони заломлення світла.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосуванням законів заломлення світла.

Дано:
\(\mathbf{\beta}=20\ ^\circ\text{С}\)

Знайти:
\(\mathbf{\alpha}\ -\ ?\)

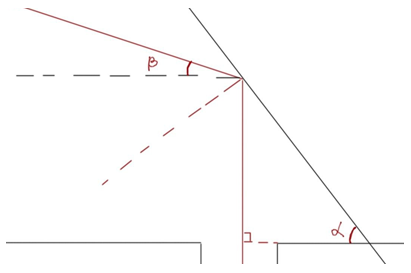
Рис. 1. Умова освітлення дна колодязя

Для того, щоби промінь міг освітити дно вузького колодязя, він має бути паралельним до його стінок, тобто перпендикулярним до горизонтальної поверхні (див. рисунок 1).

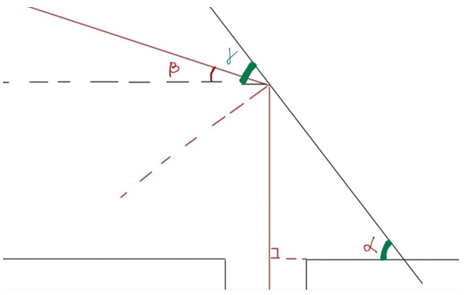
Рис. 2. Позначення кута \(\mathbf{\gamma}\)

Чорним пунктиром позначено горизонтальний напрямок. Горизонтальна поверхня паралельна до горизонту. Тож можна розглядати поверхню і чорний пунктир як дві паралельні прямі, а дзеркало як їхню січну. Тоді \(\mathbf{\alpha}=\mathbf{\gamma}\) (як відповідні кути при паралельних прямих і січній на рисунку 2).

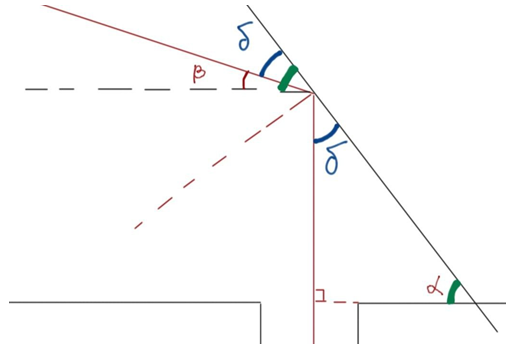
Рис. 3. Позначення кута \(\mathbf{\delta}\)

Тоді кут між падним променем і поверхнею дзеркала \(\mathbf{\delta}\) (рис. 3) дорівнює різниці кутів \(\mathbf{\alpha}\) та \(\mathbf{\beta}\): $$ \mathbf{\delta}=\mathbf{\alpha}-\mathbf{\beta}. $$

За умовою відбивання кут падіння дорівнює куту відбивання. Тому кути між падним променем і поверхнею відбивання та відбитим променем і поверхнею відбивання також рівні.

Тож маємо прямокутний трикутник із гострими кутами \(\mathbf{\alpha}\) та \(\mathbf{\delta}\):

Відповідь: 55.

ТЕМА: Квантова фізика.

Завдання скеровано на перевірку розуміння зв’язку маси та енергії.

Дано:
\(E=200\ \text{кВт}\cdot \text{год}\)

1. Знайти:
\(m\ (\text{мкг})\ -\ ?\)

Енергію, спожиту родиною, необхідно перевести в Дж:

Енергія пов’язана з масою формулою $$ E=mc^2. $$

Тоді

Відповідь: 8.