ЗНО онлайн 2019 року з фізики – основна сесія

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на оцінювання вміння застосовувати формулу залежності координат від часу для рівноприскореного руху.

Загальний вигляд залежності координати від часу за прямолінійного рівноприскореного руху виражено формулою: $$ x=x_0+v_{0x}t+\frac{a_x}{2}t^2\ \ (1), $$ де \(x_0\) – початкова координата, \(v_{0x}\) – початкова швидкість, \(a_x\) – прискорення тіла, \(t\) – час руху.

За умовою початкова швидкість \(v_{0x}=6\ \text{м/с}\), прискорення \(a_x=1\ \text{м/с}^2.\) Тож рівняння координати таке: $$ x=x_0+6t+\frac 12 t^2\ \ (2). $$

Хоча значення початкової координати невідоме, однак можна з-поміж наведених вибрати відповідь, що не суперечить виразу (2).

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на оцінювання розуміння фізичних понять, що стосуються рівномірного руху по колу, зокрема доцентрового прискорення.

Під час рівномірного руху по колу лінійна швидкість не змінюється. Проте лінійна швидкість – це скалярна величина, яку розраховують як середню шляхову швидкість криволінійного руху. Тобто твердження «лінійна швидкість не змінюється» означає, що модуль вектора швидкості під час рівномірного руху по колу залишається незмінним, натомість напрямок швидкості постійно змінюється, щоби підтримувати траєкторію руху (коло).

Вектор швидкості в кожен момент напрямлений по дотичній до кола, тож має змінювати свій напрямок під дією певного прискорення (адже дотична в кожній точці кола відрізнятиметься від дотичної в іншій точці).

Це прискорення може бути напрямлене лише перпендикулярно до вектора швидкості, адже в будь-якому іншому разі воно змінюватиме не лише напрямок, а й модуль вектора.

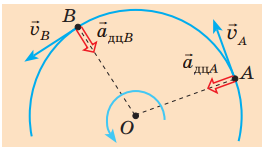
Рис. 1. Напрямок прискорення і швидкості під час руху по колу

Тож вектор прискорення під час рівномірного руху по колу завжди напрямлений до центра кола, а тому змушений змінювати свій напрямок щоразу, коли його змінює вектор швидкості. Доцентрове прискорення має постійний модуль, який можна обчислити за формулою $$ a=\frac{v^2}{r}, $$ де \(v\) – лінійна швидкість руху, \(r\) – радіус кола.

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Гука й потенціальної енергії пружини.

Потенціальну енергію \(W\) пружини обчислюють за формулою: $$ W=\frac{kx^2}{2}, $$ де \(k\) – коефіцієнт жорсткості пружини, а \(x\) – її видовження.

Оскільки відношення коефіцієнтів жорсткості пружин відоме з умови, потрібно визначити відношення обох видовжень.

Пружини розтягуються силою \(\overrightarrow{F}\), тому закон Гука для обох випадків потрібно записати так: \begin{gather*} F=-k_1x_1;\\[7pt] F=-k_2x_2. \end{gather*}

Із цих співвідношень випливає, що \begin{gather*} k_2x_2=k_1x_1\\[7pt] k_2x_2=3k_2x_1;\\[6pt] x_1=\frac{x_2}{3}. \end{gather*}

Тоді потенціальна енергія для обох пружин: \begin{gather*} W_1=\frac{k_1x_1^2}{2}=\frac{3k_2\left(\frac{x_2}{3}\right)^2}{2}=\frac 13 \frac{k_2x_2^2}{2};\\[1pt] W_2=\frac{k_2x_2^2}{2};\\[1pt] W_2=3W_1. \end{gather*}

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.

Сила, із якою тіло діє на опору чи підвіс – це вага \(\overrightarrow{P}\). Оскільки камінь лежить на гірському схилі й перебуває у стані спокою, то його вага дорівнює силі тяжіння, що діє на нього: $$ \overrightarrow{P}=m\overrightarrow{g}, $$ де \(m\) – маса тіла, \(\overrightarrow{g}\) – прискорення вільного падіння.

Сила тяжіння завжди діє в напрямку до центра Землі, тобто перпендикулярно до її поверхні. Тому, попри те, що тіло лежить на схилі під кутом до поверхі Землі, сила, із якою воно діятиме на опору, буде напрямлена вертикально вниз (рис. 1).

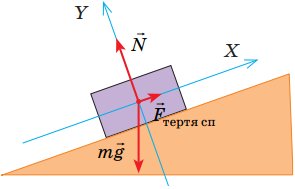
Рис. 1. Схема дії сил на тіло, що лежить на похилій поверхні

Відповідь: A.

ТЕМА: Маса. Густина. Умова плавання тіл.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про умови плавання тіл, розуміння понять густини й маси.

На шматочок льоду у воді діє виштовхувальна сила Архімеда. Тож об’єм, зафіксований до того, як лід розтанув, – це сума об’єму води й об’єму частини кубика льоду, що перебувала під водою.

Щоби шматочок льоду плавав, сила Архімеда, яка діє на його занурену частину, має дорівнювати силі тяжіння, що діє на нього: $$ F_{\text{Архімеда}}=F_{\text{тяжіння}};\ \ (1) $$

Силу тяжіння, що діє на шматочок льоду, можна розрахувати за формулою: \begin{gather*} F_{\text{тяжіння}}=mg;\ \ (2)\\[7pt] F_{\text{тяжіння}}=10\ \text{г}\cdot 10\ \frac{\text{м}}{\text{с}^2}=10^{-2}\ \text{кг}\cdot 10\ \frac{\text{м}}{\text{с}^2}=0,1\ \text{H}. \end{gather*}

Тоді можемо знайти об’єм води, витіснений цим шматком льоду, знаючи вираз для розрахунку сили Архімеда: $$ F_{\text{Архімеда}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gV,\ \ (3) $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – густина рідини, \(V\) – витіснений об’єм рідини.

Тоді можна виразити об’єм з (3): $$ V=\frac{F_{\text{Архімеда}}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}g}= \frac{0,1\ \text{H}}{1000\ \frac{\text{кг}}{\text{м}^3}}\cdot 10\ \frac{\text{м}}{\text{с}^2}=10^{-5}\ \text{м}^3=0,01\ \text{л}=10\ \text{мл}\ \ (4). $$

Тож певний рівень води в мензурці, що встановився на позначці 50 мл, зумовлений водою об’ємом 40 мл і льодом об’ємом 10 мл (він перебуває під водою і витісняє рідину).

Після того, як лід розтане, до води об’ємом 40 мл буде додано об’єм води, що утвориться з кубика льоду після його розтавання. Цей об’єм можна обчислити, знаючи, що під час танення маса речовини не змінюється, тож маса льоду дорівнюватиме масі води, що утвориться.

Вираз для густини води: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac{m}{V}.\ \ (5) $$

Тож, виразивши об’єм талої води з (5), дістанемо: $$ V=\frac{m}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}}=\frac{0,01\ \text{кг}}{1000\ \frac{\text{кг}}{\text{м}^3}}=10^{-5}\ \text{м}^3=0,01\ \text{л}=10\ \text{мл}.\ \ (6) $$

Тобто після танення льоду об’єм речовини в мензурці складається з об’єму води, що була там від початку (40 мл) і талої води об’ємом 10 мл, разом – 50 мл.

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на оцінювання розуміння процесу випаровування.

Температура речовини прямо пропорційна до її внутрішньої енергії. Тому, коли рідина охолоджується, то зменшується її внутрішня енергія.

Випаровування – це процес пароутворення з поверхні рідини, що відбувається за будь-якої температури.

Під час випаровування також зменшується внутрішня енергія тіла, адже молекули з найбільшою швидкістю покидають поверхню рідини. Ці молекули мають вищу кінетичну енергію порівняно з більшістю інших.

Внутрішню енергію можна обчислити як суму кінетичних енергій усіх молекул i потенціальних енергій їхніх взаємодій, тому втрата багатьох молекул із високою кінетичною енергією суттєво знизить її, а отже і приведе до зниження температури тіла.

Тому, якщо налити в чашку гарячий чай, то спочатку температура рідини знижуватиметься за рахунок теплообміну й випаровування. Згодом, коли чай набуде тієї самої температури, що й навколишнє середовище, теплообмін припиниться, а випаровування – ні. Тобто охолодження чаю триватиме, і його температура трохи знизиться.

Відповідь: Б.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).

Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий вологою тканиною. Вода з тканини завжди випаровується, і швидкість випаровування залежить від вологості повітря навколо. Відповідно, для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд). На рисунку 1 зображено конструкцію такого приладу. Усередині анероїда є камера з гофрованою поверхнею (1), із якої відкачано повітря. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини кріпиться стрілка (2). Тому, коли кришка камери піднімається чи опускається, пружина деформується, і стрілка починає рухатись по шкалі (3).

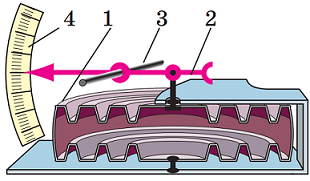
Рис. 1. Конструкція барометра-анероїда

Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується: $$ F=kx. $$

Тому, якщо відомий коефіцієнт жорсткості k пружини, то за значенням її видовження x можна визначити й силу, що його спричиняє.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на оцінювання вміння застосовувати перший закон термодинаміки до ізопроцесів.

За першим законом термодинаміки $$ Q=\triangle U+A, $$ де \(Q\) – отримане системою тепло, \(\triangle U\) – зміна внутрішньої енергії, \(A\) – виконана системою робота.

Ізотермічний процес – процес змінювання стану газу деякої маси, що відбувається за незмінної температури. Тобто $$ \triangle U=0, $$ і перший закон термодинаміки має: $$ Q=A. $$

Ізобарний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного тиску. Тоді перший закон термодинаміки має вигляд: $$ Q=\triangle U+A. $$

Ізохорний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного об’єму. Робота в такому процесі не виконується, тому перший закон термодинаміки має вигляд: $$ Q=\triangle U. $$

Адіабатний процес – це процес, який відбувається без теплообміну з навколишнім середовищем. Тобто \(Q = 0\) і перший закон термодинаміки має вигляд: $$ \triangle U+A=0. $$

А отже $$ A=-\triangle U. $$

Цей вираз описує роботу, що відбувається за рахунок зміни внутрішньої енергії.

Відповідь: A.

ТЕМА: Методи реєстрування йонізувального випромінювання. Насичена й ненасичена пара.

Завдання скеровано на оцінювання розуміння принципу роботи камери Вільсона.

Перенасичена пара – це пара, тиск якої є вищим порівняно з тиском насиченої пари за цих самих умов.

Камеру Вільсона використовують як прилад для реєстрування йонізувального випромінювання. Усередині камери зазвичай міститься пара спирту. Коли йонізувальні частинки проходять крізь камеру, за ними утворюється ланцюжок зі сконденсованих крапель. Для того, щоб ефект був помітним, пара спирту в камері має бути перенасиченою.

Для цього поршень камери швидко опускають, тим самим збільшуючи її об’єм. Через це газ всередині не встигає обмінятися теплом із середовищем, а отже має змінити свою внутрішню енергію – охолодитися. Пара, що була всередині камери, теж охолоджується. Оскільки тиск насиченої пари за зниження температури зменшується, то тиск пари спирту, тиск якої не змінився, може перевищити його. Так і утворюється перенасичена пара в камері Вільсона.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Змочування.

Завдання скеровано на оцінювання розуміння поняття змочування і вміння визначити його за виглядом краплі рідини.

Вид краплі на столі залежить від того, є рідина змочувальною чи незмочувальною.

Якщо рідина змочувальна, то сила взаємодії молекул рідини з молекулами поверхні є більшою, ніж сила взаємодії між сусідніми молекулами рідини. А якщо рідина незмочувальна, то навпаки. Тоді в капілярах поруч зі стінками рідина буде прагнути до того, щоби розтектися по його стінках, тому утворюватиметься увігнутий купол (меніск). Коли поверхня води рівна, то її потенціальна енергія мінімальна, а утворений увігнутий купол збільшує її. Рідина завжди прямуватиме до мінімуму потенціальної енергії, тобто вона намагатиметься вирівнятись, а тому підніматиметься вгору по капіляру.

Для незмочувальної рідини процес відбувається у зворотному напрямку, тому утворюється опуклий меніск і стовпчик рідини в капілярі опускається нижче.

Отже рідина, описана в завданні, – незмочувальна.

Незмочувальні рідини на поверхнях намагаються утворити сферичні краплі і зменшити площу контактування з поверхнею, але під дією сили тяжіння вони трохи деформуються, і замість однієї точки контактування з поверхнею (як у разі сфери), виникає невеликий зріз.

Відповідь: B.

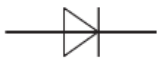
ТЕМА: Електричне коло.

Завдання скеровано на оцінювання знання умовних позначень для створення схем електричних кіл:

A – котушка індуктивності, соленоїд

Б – конденсатор

B – напівпровідниковий діод

Г – батарея гальванічних елементів

або

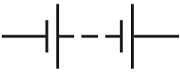
Відповідь: Б.

ТЕМА: Основи електростатики. Електричний заряд.

Завдання скеровано на оцінювання розуміння перерозподілення заряду під час контактування двох провідників.

Негативно заряджена кулька має надлишок електронів, а позитивно заряджена – дефіцит їх. Якщо з’єднати кульки провідником, то електрони рівномірно розподіляться по обох кульках, тому заряд двох з’єднаних кульок становитиме: $$ q_{\text{з'єднання}}=q_1+q_2=-5\ \text{нКл}+3\ \text{нКл}=-2\ \text{нКл}. $$

Після того як провідник приберуть, електрони нікуди не перемістяться і залишаться розподіленими рівномірно по всій системі. Оскільки кульки однакові, то заряд кожної кульки окремо дорівнюватиме половині всього заряду з’єднаних кульок: $$ q_{1\ \text{після}}=\frac{q_{\text{з'єднання}}}{2}=-1\ \text{нКл}. $$

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.

Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.

Нехай \(I\) – сила струму, що проходить у колі, а \(U\) – напруга в ньому. Коло складено з двох послідовно з’єднаних пар резисторів, що підключено паралельно. Оскільки пари резисторів з’єднано послідовно, то в кожній із них сила струму дорівнюватиме силі струму в колі: $$ I_{\text{пара 1}}=I_{\text{пара 2}}=I. $$

Напругу в колі можна обчислити як суму напруг на кожній із пар: $$ U=U_{\text{пара 1}}+U_{\text{пара 2}}. $$

Усередині кожної пари резистори з’єднано послідовно, тому сила струму в парі дорівнюватиме сумі сил струму на кожному з резисторів: \begin{gather*} I_{\text{пара 1}}=I_{R=6\ \text{Ом}}+I_{R=3\ \text{Ом}};\\[7pt] I_{\text{пара 2}}=I_{R=24\ \text{Ом}}+I_{R=8\ \text{Ом}}. \end{gather*}

Напруга на кожному резисторі дорівнює напрузі на всій парі: \begin{gather*} U_{\text{пара 1}}=U_{R=6\ \text{Ом}}=U_{R=3\ \text{Ом}};\\[7pt] U_{\text{пара 2}}=U_{R=24\ \text{Ом}}=U_{R=8\ \text{Ом}}. \end{gather*}

Опір кожної пари резисторів розраховують за правилами паралельного з’єднання провідників: \begin{gather*} \frac{1}{R_{\text{пара 1}}}=\frac{1}{R_1}+\frac{1}{R_2};\\[6pt] \frac{1}{R_{\text{пара 2}}}=\frac{1}{R_3}+\frac{1}{R_4};\\[6pt] R_{\text{пара 1}}=\frac{R_1R_2}{R_1+R_2}=\frac{6\ \text{Ом}\cdot 3\ \text{Ом}}{6\ \text{Ом}+3\ \text{Ом}}=2\ \text{Ом};\\[6pt] R_{\text{пара 2}}=\frac{R_3R_4}{R_3+R_4}=\frac{24\ \text{Ом}\cdot 8\ \text{Ом}}{24\ \text{Ом}+8\ \text{Ом}}=6\ \text{Ом}. \end{gather*}

Тоді можна розрахувати напругу на кожній парі за законом Ома: \begin{gather*} I=\frac UR;\\[6pt] U_{\text{пара 1}}=I_{\text{пара 1}}R_{\text{пара 1}}=IR_{\text{пара 1}}=2I\ (\text{В});\\[7pt] U_{\text{пара 2}}=I_{\text{пара 2}}R_{\text{пара 2}}=IR_{\text{пара 2}}=6I\ (\text{В}). \end{gather*}

Тоді за законом Ома можна обчислити силу струму на кожному з резисторів: \begin{gather*} I_{R=6\ \text{Ом}}=\frac{U_{R=6\ \text{Ом}}}{R_1}=\frac{U_{\text{пара 1}}}{R_1}=\frac{2I}{6}=\frac 13 I;\\[6pt] I_{R=3\ \text{Ом}}=\frac{U_{R=3\ \text{Ом}}}{R_2}=\frac{U_{\text{пара 1}}}{R_2}=\frac{2I}{3}=\frac 23 I;\\[6pt] I_{R=24\ \text{Ом}}=\frac{U_{R=24\ \text{Ом}}}{R_2}=\frac{U_{\text{пара 2}}}{R_3}=\frac{6I}{24}=\frac 14 I;\\[6pt] I_{R=8\ \text{Ом}}=\frac{U_{R=8\ \text{Ом}}}{R_4}=\frac{U_{\text{пара 2}}}{R_4}=\frac{6I}{8}=\frac 34 I. \end{gather*}

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Електростатичний потенціал.

Завдання скеровано на оцінювання розуміння понять електростатичного потенціалу, різниці потенціалів і роботи електричного поля з перенесення заряду.

Поле не виконує роботу під час переміщення заряду, якщо воно відбувається по еквіпотенціальній поверхні.

Еквіпотенціальна поверхня – це поверхня, у всіх точках якої потенціал електростатичного поля має однакове значення (рис. 1).

Тому необхідно знайти точку на тій самій еквіпотенціальній поверхні, що й початкова точка. Еквіпотенціальні поверхні перпендикулярні до силових ліній поля. Тому, якщо провести перпендикулярну до силових ліній пряму через точку 1, то будь-яке переміщення вздовж неї не вимагатиме від поля виконання роботи.

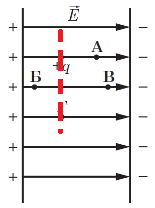
Рис. 1. Зображення еквіпотенціальної поверхні (червоним)

Відповідь: Г.

ТЕМА: Електричний струм у різних середовищах. Електричний струм у напівпровідниках. Електронно-дірковий перехід.

Завдання скеровано на оцінювання розуміння принципу роботи p-n переходу й основних його особливостей.

Зменшення опору зі збільшенням температури й освітленості є важливими особливостями напівпровідників.

p-n-Перехід – це ділянка контакту двох напівпровідників із різними типами провідності. Їхньою головною особливістю є одностороння провідність. Під час прямого підключення p-напівпровідник із дірковою провідністю з’єднують із позитивним полюсом джерела, а n-напівпровідник – із негативним полюсом. У такому разі електрони з напівпровідника n-типу рухаються до позитивного полюса джерела, а дірки з напівпровідника p-типу рухаються до негативного полюса джерела. Цей рух проходить крізь p-n перехід, а отже потоку електронів у колі від одного полюса джерела до іншого нічого не заважає (рис. 1).

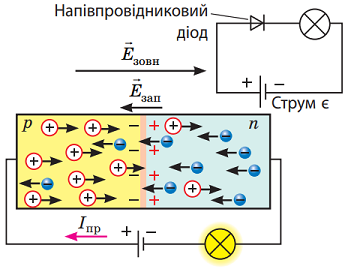
Рис. 1. Процеси в p-n переході під час прямого підключення

Якщо p-n перехід до джерела навпаки (негативний полюс до напівпровідника p-типу, а позитивний до напівпровідника n-типу), то дірки й електрони знову почнуть рухатися до протилежних полюсів джерела, але цього разу рух відбувається не крізь p-n перехід, а навпаки. Тому потік електронів між полюсами джерела в колі майже зупиняється (рис. 2).

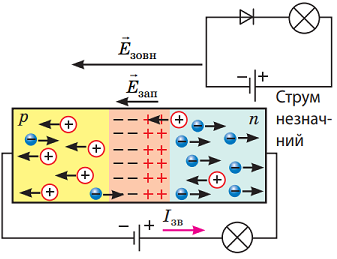
Рис. 2. Процеси в p-n переході під час зворотного підключення

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Електрорушійна сила.

Завдання скеровано на оцінювання розуміння поняття електрорушійної сили.

Електрорушійна сила \(E\) джерела струму – скалярна фізична величина, яка характеризує енергетичні властивості джерела струму й дорівнює відношенню роботи сторонніх сил із переміщення позитивного заряду \(q\) всередині джерела до значення цього заряду.

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення

Завдання скеровано на оцінювання розуміння законів збереження енергії і меж їхньої застосовності.

Нехай \(m_1\) – маса кулі 1, а \(m_2\) – маса кулі 2, і нехай до удару швидкість кулі 1 – \(v_1\).

Затим потрібно розглянути три положення кулі 2. У точці A швидкість дорівнюватиме \(v(A)\), у точці B – \(v(B)\) і в точці C – \(v(C)\). Точки A й C – це крайні точки коливання кулі 2, у них вона змінює напрямок свого руху, отже \(v(A) = v(С) = 0\). Точка B – середина відрізка AC, тому швидкість руху кулі в цій точці максимальна, а \(v(B) – v_{max}\).

За законом збереження кінетичної енергії сума кінетичної енергії до зіткнення двох куль дорівнюватиме її сумі після. Тому потрібно розглянути два варіанти: перший для точок A й C, де швидкість кулі 2 дорівнює нулю, і другий для точки B, де її швидкість максимальна.

Для A й C: \begin{gather*} \frac{m_1v_1^2}{2}=\frac{m_1v_1^{'2}}{2}+\frac{m_2v_2^{'2}};\\[6pt] v_2^{'}=\sqrt{\frac{m_1(v_1^2-v_1^{'2})}{m_2}}. \end{gather*}

Для B: \begin{gather*} \frac{m_1v_1^2}{2}+\frac{m_2v_2^2}{2}=\frac{m_1v_1^{'2}}{2}+\frac{m_2v_2^{'2}};\\[6pt] v_2^{'}=\sqrt{\frac{m_1(v_1^2-v_1^{'2})}{m_2}+v_2^2}. \end{gather*}

Вираз \(v_2^{'}\) для точки B завжди буде більшим, ніж вираз для точок A й C, якщо швидкість першої кулі однакова в усіх ситуаціях.

Відповідь: Б.

ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на оцінювання вміння застосовувати формулу Томсона.

Період електромагнітних коливань у контурі можна визначити за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.

Тоді в положенні 1 період дорівнюватиме: $$ T_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{4LC}=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}. $$

А в положенні 2: $$ T_2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}. $$

Тобто: $$ T_1=2T_2. $$

Відповідь: A.

ТЕМА: Оптика. Прямолінійність поширення світла в однорідному середовищі.

Завдання скеровано на оцінювання розуміння принципів освітлення точковими і протяжними джерелами.

Півтінь – це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.

Якщо джерело світла точкове й випромінює в усіх напрямках, то та частина променів, що потрапляє на непрозоре тіло, ніяк не може потрапити у простір за ним (рис. 1).

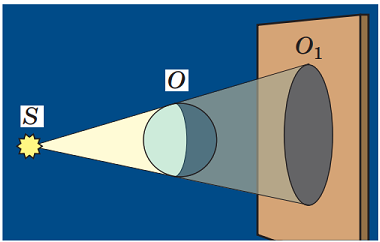
Рис. 1. Утворення повної тіні під час освітлювання точковим джерелом

Якщо тіло освічують кілька точкових джерел, то для кожного з них відбувається те саме. Але оскільки джерела розташовані на певній відстані одне від одного, то кути, під якими утворюватимуться конуси їхніх тіней, трохи відрізнятимуться. Там, де всі конуси перекриваються, утворюється тінь, а в усіх інших областях (де перекривається лише частина конусів або й узагалі лише один) утворюється півтінь (рис. 2).

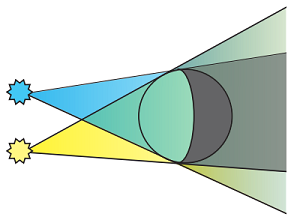
Рис. 2. Утворення півтіні під час освітлення кількома точковими джерелами

Коли джерело протяжне, то можна вважати кожну точку його площі окремим точковим джерелом, тому за такого освітлення також утворюватиметься півтінь (рис. 3).

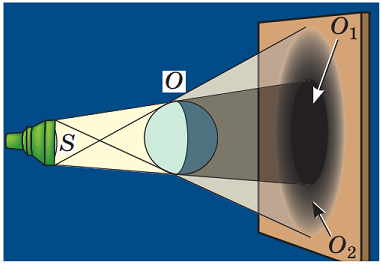
Рис. 3. Утворення півтіні під час освітлення протяжним джерелом

Відповідь: Б.

ТЕМА: Оптика. Закони відбивання заломлення і поглинання світла. Лінза. Дифракційна ґратка.

Завдання скеровано на оцінювання вміння застосовувати знання про дифракцію і закони геометричної оптики під час аналізу прикладів із життя.

Дифракція – це явище огинання хвилями перешкод.

У разі проходження крізь лінзу фотоапарата електромагнітна хвиля заломлюється, тобто всі процеси відбуваються за законами геометричної оптики. Натомість дифракція – це явище хвильової оптики.

Світлофільтр поглинає частину електромагнітних хвиль, які потрапляють на нього, у результаті чого він пропускає частоти лише певного діапазону. Огинання перешкод у цьому процесі не відбувається.

Під час рентгеноструктурного аналізу рентгенівський промінь падає на кристалічну ґратку. Її можна розглядати як природну дифракційну ґратку, у якій відстані між атомами є прозорими ділянками, а самі атоми – непрозорими. У цьому разі відбувається дифракція, і за утвореною дифракційною картиною аналізують досліджувану поверхню.

Під час перегляду стереофільмів одночасно транслюють дві версії фільму, зняті під невеликим кутом одна до одної. За допомогою окулярів зі спеціальними фільтрами зображення, зняте для лівого ока, блокують на правому й навпаки. Після чого мозок обробляє два різних зображення, отримані з двох очей, і збирає об’ємну картину. Дифракція при цьому не відбувається.

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Система відліку. Швидкість.

Завдання скеровано на оцінювання розуміння понять швидкості світла й системи відліку.

Значення швидкості світла є сталим для будь-якої системи відліку незалежно від швидкості її руху.

Тому не залежно від того, яке тіло відліку вибрано (Земля, станція чи ракета), значення швидкості світла буде однаковим – 300 000 км/с.

Відповідь: A.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання вміння застосовувати знання про фотоефект і його особливості під час аналізування роботи приладів, на ньому заснованих (фоторезисторів).

Фоторезистор – це прилад для вимірювання освітленості. Принцип його роботи ґрунтується на залежності провідності напівпровідників від освітленості.

Опір напівпровідників зменшується зі збільшенням освітленості, тому фоторезистор у темряві матиме більший опір, ніж освітлений.

Опір фоторезисторів а і б можна визначити за законом Ома: $$ I=\frac{U}{R}. $$

Значення сили струму \(I\) й напруги \(U\) можна дізнатися з графіка. На графіку, наведеному в умові завдання, не зазначено одиниці вимірювання напруги й сили струму, тому можна вважати, що їх вимірюють в умовних одиниця (у.о. \(I\)
й у.о. \(U\) відповідно).

Для зручності потрібно визначити сили струму для напруги 3 у.о. \(U\) \begin{gather*} U_a=U_b=3\ \text{у.о.}U;\\[7pt] I_a=3\ \text{у.о.}I;\\[7pt] I_b=1\ \text{у.о.}I.\\[7pt] \end{gather*}

Тоді можна розрахувати опір, одиницею якого є умовна одиниця опору (у.о. \(R\)): \begin{gather*} R_a=\frac{U_a}{I_a}=\frac{3\ \text{у.о.}U}{3\ \text{у.о.}I}=1\ \text{у.о.}R;\\[6pt] R_b=\frac{U_b}{I_b}=\frac{3\ \text{у.о.}U}{1\ \text{у.о.}I}=3\ \text{у.о.}R;\\[6pt] R_b=3R_a. \end{gather*}

Тому \(b\) – це фоторезистор у темряві, а \(a\) – освітлений.

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.

Завдання скеровано на оцінювання розуміння постулатів Бора і їхнього застосування для опису процесів випромінювання і поглинання.

Модель атома Бора є вдосконаленням планетарної моделі. Один із головних недоліків планетарної моделі такий:
якщо описувати рух електронів навколо ядра законами класичної механіки, то вони б постійно наближались до ядра і з часом упали б на нього. Такий атом не може існувати.

Тому Бор сформулював постулати:

1) атомна система може перебувати лише в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; у стаціонарному стані атом не випромінює енергію;

2) під час переходу з одного стаціонарного енергетичного стану (з енергією \(E_k\)) в інший (з енергією \(E_n\)) атом випромінює або поглинає квант електромагнітної енергії: $$ hv=|E_k-E_n|. $$

Квант електромагнітної хвилі має специфічну частоту, для видимого випромінювання це означає, що випромінений квант на спектрах випромінювання виглядає як вузька кольорова смужка. У спектрі поглинання поглинутий квант виглядає як вузька темна смужка (рис. 1).

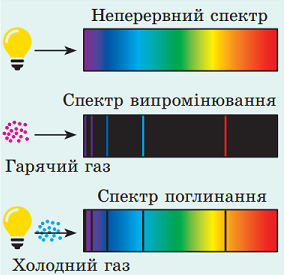
Рис. 1. Вигляд лінійчастих спектрів поглинання і випромінювання

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Сила. Момент сили. Потенціальна енергія.

Завдання скеровано на оцінювання вміння пояснювати щоденні процеси за допомогою фізичних законів.

У завданні наведено такі формули:

А Вираз для опису роботи сили тяжіння.

Б Вираз для потенціальної енергії деформованого тіла.

В Вираз для визначення сили тертя.

Г Рівняння моментів сил для стану рівноваги.

Д Вираз для закону Архімеда.

1 Під час розтягування гумової нитки виникає сила пружності, тож розтягування можна описати виразом для потенціальної енергії деформованого тіла (Б).

2 Під час падіння поле тяжіння Землі виконує роботу над тілом. Тому цей процес можна описати виразом для роботи сили тяжіння (А).

3 Під час ковзання черевика по підлозі між ними виникає сила тертя ковзання, що можна описати виразом В.

4 Тіло перебуватиме в положенні рівноваги (плаватиме на поверхні, у товщі рідини або на дні), якщо сила Архімеда, що виштовхує його з рідини, дорівнюватиме силі тяжіння, що діє на нього. Тому процес можна описати виразом Д.

Відповідь: 1Б, 2А, 3В, 4Д.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її зміни. Способи теплопередачі.

Завдання скеровано на оцінювання розуміння різних механізмів теплопередачі й уміння виявляти необхідний механізм теплопередачі в щоденних ситуаціях.

1 Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу. Прикладом застосування конвекції є принцип обігрівання приміщень радіаторами. Радіатори передають тепло найближчим шарам повітря. Густина теплих шарів повітря зменшується, і вони починають підніматися вгору, витісняючи холодніші шари повітря вниз, де вони починають нагріватися. Під час підйому теплі шари повітря також передають тепло холоднішим. Коли ж вони досягають верху приміщення, стають суттєво холоднішими за шари повітря, тільки-но нагріті радіаторами. Тож конвекція триває.

2 Теплопровідність – це вид теплопередачі, зумовлений хаотичним рухом частинок речовини й не супроводжуваний перенесенням цієї речовини. Теплопровідність – це один із основних способів утрати теплоти в організмів. Саме тому організми, особливо морські тварини, часто мають прошарок жиру під шкірою. Адже питома теплоємність води майже вчетверо більша, ніж питома теплоємність повітря, а отже змушуватиме тіла віддавати більше енергії.

3 Механічна робота – це фізична величина, яка характеризує зміну механічного стану тіла. Одним із найпоширеніших прикладів зміни внутрішньої енергії в результаті виконання роботи є нагрівання під час тертя.

4 Випромінювання – це вид теплопередачі, за якого енергія передається за допомогою електромагнітних хвиль. Сонячні промені – це сукупність електромагнітних хвиль різної частоти. Коли вони досягають поверхні, то вона поглинає їх. Унаслідок цього збільшується її внутрішня енергія і температура.

Відповідь: 1В, 2Б, 3А, 4Г.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання розуміння принципів роботи напівпровідникових приладів і вольтметра.

1 Термістор – це напівпровідниковий прилад для контролювання температури. Принцип його роботи базується на тому, що в напівпровідників зі збільшенням температури зменшується питомий опір, тому зміна температури приводить до зміни провідності.

2 Сонячна батарея – це прилад для перетворення сонячної енергії на електричну. Вони зазвичай складаються з напівпровідникових фотоелементів, що працюють на внутрішньому фотоефекті. Сонячні промені вибивають із напівпровідника n-типу електрони, і вони рухаються до напівпровідника p-типу, де об’єднуються з дірками в пари. Між p-напівпровідником і n-напівпровідником у результаті цього утворюється різниця потенціалів.

3 Вакуумний діод – це прилад з однобічною провідністю, що складається з резервуару, у якому утворено вакуум, і двох електродів. У резервуарі катод нагрівається ниткою розжарення, у результаті чого деякі електрони катода отримують кінетичну енергію, більшу за роботу виходу матеріалу. Тоді вони покидають катод. Якщо катод підключено до негативного полюса джерела, а анод – до позитивного, то електрони, що утворилися внаслідок термоелектронної емісії, починають рухатися до анода, тобто через діод тече струм. Якщо полюси джерела підключити навпаки, то електрони затримуватиме поле на катоді.

4 Стрілочний вольтметр – це прилад для вимірювання напруги. Він складається з постійного магніту, усередині якого закріплено рамку. За підключення вольтметра в коло зі струмом по рамці починає текти струм, вона обертається. Обертання рамки зі струмом під дією магнітного поля постійного магніту через спеціальні кріплення, що складаються зі спіральних пружин і півосей, передаються стрілці, яка вказує на значення на шкалі.

Відповідь: 1Г, 2А, 3В, 4Д.

ТЕМА: Оптика. Світло, як електромагнітна хвиля.

Завдання скеровано на оцінювання розуміння принципів поширення світла крізь різні середовища й оптичні прилади.

1 Природне світло складається з багатьох хвиль, випромінених різними атомами. Через це в пучку природного світла існує безліч напрямків коливання вектора напруженості електричного поля. Під час поляризації замість хаотичного розподілу напрямків у пучку світла залишається лише той напрямок (або напрямки), які потрібні. Для поляризації використовують спеціальні фільтри – поляроїди (або поляризатори, рис. 1).

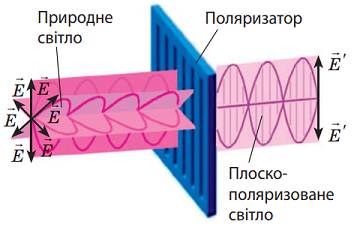
Рис. 1. Принцип роботи поляризатора

Поляризатор працює як щілина, що пропускає лише коливання певного напрямку. Якби електромагнітні хвилі були поздовжніми, то поляризатор не вносив би ніяких змін, але зафіксовано зміни в інтенсивності в експериментах (адже велика частина променів відбивається поляризатором). Тому світло може бути лише поперечною хвилею.

2 Світло, що падає на більшість предметів навколо, відбивається від них. Відбиті промені потрапляють на око, фокусуються кришталиком на сітківку, звідки сигнали через зоровий нерв передаються на обробку в мозок.

3 Принцип роботи лінзи полягає в заломленні променів на двох вигнутих поверхнях. Залежно від типу лінзи й початкової форми променя після проходження лінзи пучок може сфокусуватися в певній точці, розсіятися чи навіть стати паралельним. На рисунку 2 схематично зображено принцип роботи збиральної лінзи, на яку падає паралельний пучок.

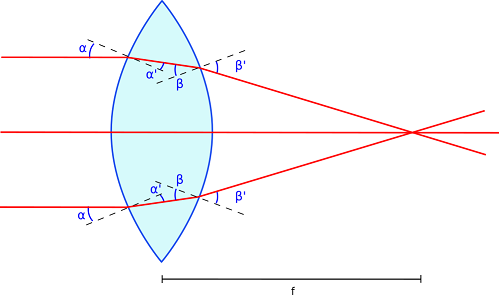
Рис. 2. Принцип роботи збиральної лінзи

4 Сонце – це одне з найбільш широкочастотних джерел випромінювання. Воно випромінює всі електромагнітні хвилі – від радіохвиль і до γ-випромінювання. Через це спектр сонця неперервний. Проте деякі гази поглинають кванти світла з дуже специфічними частотами. Тоді в неперервному спектрі утворюються темні смуги на місці цих поглинутих квантів (рис. 3).

Рис. 3. Вигляд лінійчастих спектрів поглинання

Відповідь: 1В, 2Г, 3Д, 4Б.

ТЕМА: Механіка. Закони збереження в механіці.

Завдання скеровано на оцінювання розуміння понять імпульсу руху, кінетичної енергії й уміння використовувати закони збереження.

Дано:
\(m_{\text{платф}}=20\ \text{т}\)
\(m_{\text{слон}}=5\ \text{т}\)
\(v_{\text{слон після}}=2\ \text{м/с}\)

1. Знайти:
\(v_{\text{платф після}}\ -\ ?\)

За законом збереження імпульсу, коли слон починає рухатися, то платформа також має почати рухатися. Швидкість платформи буде напрямлено в протилежний від швидкості руху слона бік. Адже до початку руху імпульс як платформи, так і самого слона дорівнює нулю, бо нулю дорівнюють їхні швидкості.

Імпульс розраховують за формулою $$ \overrightarrow{p}=m\overrightarrow{v}, $$ де \(m\) – це маса тіла, а \(\overrightarrow{v}\) – його швидкість.

Для розрахунку імпульсу платформи необхідно враховувати як її власну масу, так і масу слона на ній, тоді за законом збереження імпульсу \begin{gather*} (m_{\text{платф}}+m_{\text{слон}})\overrightarrow{v}_{\text{платф до}}+m_{\text{слон}}\overrightarrow{v}_{\text{слон до}}=\\[7pt] (m_{\text{платф}}+m_{\text{слон}})\overrightarrow{v}_{\text{платф після}}\overrightarrow{v}_{\text{слон після}}+m_{\text{слон}}\overrightarrow{v}_{\text{слон після}}=0;\\[7pt] (m_{\text{платф}}+m_{\text{слон}})\overrightarrow{v}_{\text{платф після}}=-m_{\text{слон}}\overrightarrow{v}_{\text{слон після}}. \end{gather*}

Після проєктування попереднього рівняння на напрямок руху слона можна скласти такі вирази: \begin{gather*} (m_{\text{платф}}+m_{\text{слон}})v_{\text{платф після}}=m_{\text{слон}}v_{\text{слон після}};\\[6pt] v_{\text{платф після}}=\frac{m_{\text{слон}}v_{\text{слон після}}}{(m_{\text{платф}}+m_{\text{слон}})}=\frac{5\ \text{т}\cdot 2\ \text{м/с}}{25\ \text{т}}=0,4\ \text{м/с}. \end{gather*}

2. Знайти:
\(E_{\text{кін плат}}\ -\ ?\)

Кінетичну енергію можна обчислити за виразом: $$ E_{\text{кін}}=\frac{mv^2}{2}. $$

Кінетична енергія платформи залежить тільки від її власної маси і швидкості, якої вона набула після того як слон почав рухатися: \begin{gather*} E_{\text{кін плат}}=\frac{mv^2}{2}=\frac{20\ \text{т}\cdot (0,4\ \text{м/с})^2}{2}=\\[6pt] =\frac{20000\ \text{кг}\cdot (0,4\ \text{м/с})^2}{2}=1600\ \text{Дж}=1,6\ \text{кДж}. \end{gather*}

Відповідь: 1. 0,4. 2. 1,6.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння теплового балансу. Робота. Потужність. Коефіцієнт корисної дії (ККД).

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі, що поєднують у собі використання понять роботи, потужності й рівняння теплового балансу.

Дано:
\(P=4,6\ \text{кВт}\)
\(\triangle t=10\ ^\circ\text{С}\)
\(\triangle \tau=10\ \text{хв}\)
\(m=6\ \text{кг}\)
\(c=460\ \text{Дж}/(\text{кг}\cdot \text{К})\)

1. Знайти:
\(Q(\text{кДж})\ -\ ?\)

Виділена під час тертя теплота витрачається на нагрівання верстата, тому можна скористатися рівнянням теплового балансу для її визначення: $$ Q=cm\triangle t=460\frac{\text{Дж}}{\text{кг}\cdot \text{К}}\cdot 6\ \text{кг}\cdot 10\ ^\circ\text{С}=27600\ \text{Дж}=27,6\ \text{кДж}. $$

2. Знайти:
\(\text{ККД}_{max}(\text{%})\ -\ ?\)

ККД можна визначити як відношення виконаної тепловою машиною роботи \(A\) до отриманої нею енергії \(Q\): $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}. $$

Кількість енергії, що отримує верстат від двигуна, можна обчислити за його потужністю: $$ P=\frac{Q_{\text{вит}}}{\tau}, $$ де \(Q_{\text{вит}}\) – витрачена верстатом енергія, а \(\tau\) – час роботи верстата.

\begin{gather*} Q_{\text{вит}}=P\tau=4,6\ \text{кВт}\cdot 10\ \text{хв}=4600\ \text{Вт}\cdot 600\ \text{с}=\\[7pt] =2760000\ \text{Дж}=2760\ \text{кДж}. \end{gather*}

На виконання корисної роботи \(A\) піде вся енергія, передана верстату двигуном крім тої, що буде витрачена на нагрівання від тертя, тому: $$ A=Q_{\text{вит}}-Q=2760\ \text{кДж}-27,6\ \text{кДж}=2732,4\ \text{кДж}. $$

Тоді ККД дорівнюватиме: $$ \text{ККД}=\frac{A}{Q_{\text{вит}}}\cdot 100\ \text{%}=\frac{2732,4\ \text{кДж}}{2760\ \text{кДж}}\cdot 100\ \text{%}\approx 99\ \text{%}. $$

Відповідь: 1. 27,6. 2. 99.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на закон Ома для повного кола, а також уміння читати схеми електричного кола.

Дано:
\(r=1\ \text{Ом}\)

1. Знайти:
\(R_{\text{рис. 2}}\ -\ ?\)

Реостат – це елемент кола зі змінним опором. Зазвичай реостат – це довгий провідник, повзунок якого дає змогу включити в коло його частину будь-якої довжини. Чим меншу частину реостата включено в коло, тим менший його опір. Опір провідника можна визначити за його геометричними параметрами: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – питомий опір провідника, \(l\) – його довжина, \(S\) – площа його перерізу.

Фізичну будову реостата відображено й у його символі для схематичного зображення електричного кола. Стрілка в позначенні реостата показує, яку саме його частину включено в коло.

За умовою завдання максимальний опір реостата відповідає крайньому правому положенню. За рисунком 1 можна визначити, що довжина провідника в цьому разі становить 6 клітинок. Масштаб рисунка не зазначено, тому можна вважати, що довжина реостата – 6 умовних одиниць довжини (у. о. д.). На рисунку 2 в коло включено половину реостата. Ні питомий опір провідника, ні його поперечний переріз при цьому не відрізняються від ситуації, коли опір максимальний. Лише довжина провідника вдвічі менша, тож можна обчислити опір реостата в положенні на рисунку 2:

2. Знайти:
\(\frac{l_{\text{рис. 2}}}{l_{\text{рис. 1}}}\ -\ ?\)

Аналогічно можна розрахувати опір реостата для положення на рис. 1: \begin{gather*} R_{\text{рис. 2}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_{\text{рис. 1}}}{S}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{1\ \text{у. о. д.}}{S}=1\ \text{у. о. д.};\\[6pt] 1\ \frac{\text{Ом}}{\text{у. о. д.}}=1\ \text{Ом}. \end{gather*}

За законом Ома для повного кола можна визначити силу струму: $$ I=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R+r}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\) – електрорушійна сила джерела, \(r\) – внутрішній опір джерела, \(R\) – опір зовнішньої ділянки кола.

Тоді для рисунків 1 і 2: \begin{gather*} I_{\text{рис. 1}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R_{\text{рис. 1}}+r}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{1\ \text{Ом}+1\ \text{Ом}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{2\ \text{Ом}};\\[6pt] I_{\text{рис. 2}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R_{\text{рис. 2}}+r}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{3\ \text{Ом}+1\ \text{Ом}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{4\ \text{Ом}};\\[6pt] I_{\text{рис. 2}}/I_{\text{рис. 1}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{4\ \text{Ом}}/\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{2\ \text{Ом}}=0,5. \end{gather*}

Відповідь: 1. 3. 2. 0,5.

ТЕМА: Магнітне поле, електромагнітна індукція. Трансформатор.

Завдання скеровано на оцінювання розуміння принципів роботи трансформатора й уміння розв’язувати розрахункові задачі відповідного змісту.

Дано:
\(U_1 = 220\ \text{В}\)
\(U_2 = 11000\ \text{В}\)
\(N_{\text{перв}}=40\)

1. Знайти:
\(k\ -\ ?\)

Описаний в умові трансформатор – підвищувальний, отже коефіцієнт трансформації \(k\lt 1\). Його можна обчислити як відношення початкової напруги до кінцевої: $$ k=\frac{U_1}{U_2}=\frac{220\ \text{В}}{11000\ \text{В}}=0,02. $$

Якщо розімкнути іншу обмотку трансформатора, то первинною вважатимуть обмотку з напругою \(11000\ \text{В}\), а вторинною – із напругою \(220\ \text{В}\). У такому разі коефіцієнт трансформації можна обчислити як відношення напруги на первинній обмотці до напруги на вторинній обмотці: $$ k=\frac{U_2}{U_1}=\frac{11000\ \text{В}}{220\ \text{В}}=50 $$

Такий трансформатор знижуватиме напругу, а за умовою напруга має підвищуватися, тому для подальшого розв’язку потрібно використати коефіцієнт трансформації \(k=0,02\).

2. Знайти:
\(N_{\text{втор}}\ -\ ?\)

Також коефіцієнт трансформації можна обчислити як відношення кількості мотків у первинній обмотці до кількості мотків у вторинній: $$ k=\frac{N_{\text{перв}}}{N_{\text{втор}}}. $$

Тоді $$ N_{\text{втор}}=\frac{N_{\text{перв}}}{k}=\frac{40}{0,05}=2000. $$

Відповідь: 1. 0,02 або 50. 2. 2000.

ТЕМА: Гідростатичний тиск

Завдання скеровано на оцінювання розуміння понять атмосферного й гідростатичного тиску, уміння розв’язувати розрахункові задачі, пов’язані з ними.

Дано:
\(N=101\)
\(g=10\ \text{м/с}^2\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=1,3\ \text{кг/м}^3\)
\(h_{1\ \text{поверху}}=3\ \text{м}\)

Знайти:
\(\triangle p\ -\ ?\)

Атмосферний тиск – це тиск повітря над рівнем, де його вимірюють. Тому тиск на першому поверсі буде більшим від тиску на 101-му поверсі саме на значення тиску стовпа повітря висотою 100 поверхів. Тиск нерухомого повітряного стовпа – це гідростатичний тиск. Його визначають за формулою: $$ p=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gh. $$

Тоді висота повітряного стовпа, утвореного 100 поверхами дорівнюватиме: $$ h=(N-1)\cdot h_{1\ \text{поверху}}=100\cdot 3\ \text{м}=300\ \text{м}. $$

І гідростатичний тиск цього повітряного стовпа: $$ \triangle p=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gh =1,3\ \frac{\text{кг}}{\text{м}^3}\cdot 10\ \frac{\text{м}}{\text{с}^2}\cdot 300\ \text{м}=3900\ \text{Па}=3,9\ \text{кПа}. $$

Відповідь: 3,9.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Сила тертя

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рвномірного руху по колу.

Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_1=0,72\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_2=0,18\)

Знайти:
\(\frac{v_1}{v_2}\ -\ ?\)

Можна вважати, що під час повертання машина рухається по ділянці кола (рис. 1).

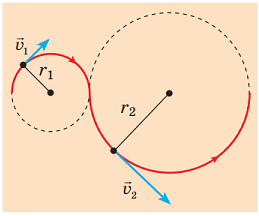
Рис. 1. Зображення поворотів як елементів кола під час криволінійного руху

Під час такого руху швидкість автомобіля спрямовано по дотичній до кола. Оскільки під час руху по колу швидкість постійно змінює свій напрямок, виникне доцентрове пришвидшення.

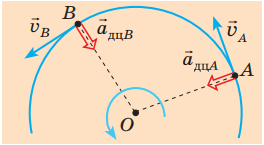
Рис. 2. Напрямок пришвидшення і швидкості під час руху по колу

За другим законом Ньютона рівнодійна сил дорівнює добутку маси тіла на пришвидшення, набуте під час взаємодії, тобто $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на автомобіль у площині напрямку руху є сила тертя, тому другий закон Ньютона в цьому разі можна записати так: $$ \overrightarrow{F_{\text{тер}}}=m\overrightarrow{a_{\text{доц}}}. $$

Силу тертя визначають за формулою $$ \overrightarrow{F_{\text{тер}}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}\overrightarrow{N}, $$ де \(\overrightarrow{N}\) – сила реакції опори.

Її можна визначити, записавши другий закон Ньютона для осі OY. Уздовж цієї осі на машину діє сила тяжіння і сила реакції опори, але рух не відбувається, а отже рівнодійна дорівнює нулю: \begin{gather*} \overrightarrow{F_{\text{тяж}}}+\overrightarrow{N}=0;\\[7pt] F_{\text{тяж}}-N=0;\\[7pt] F_{\text{тяж}}=N=mg. \end{gather*}

Тоді сила тертя дорівнюватиме: $$ F_{\text{тер}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}mg. $$

Сила тертя завжди заважає рухові. Оскільки швидкість автомобіля спрямована з кола, то сила тертя буде спрямована до його центра. Крім сили тертя, можна також обчислити доцентрове пришвидшення, виразивши його за допомогою швидкості руху автомобіля і радіуса повороту: $$ a_{\text{доц}}=\frac{v^2}{R}. $$

Тоді можна перетворити рівняння: \begin{gather*} F_{\text{тер}}=ma_{\text{доц}};\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}mg=m\frac{v^2}{R}. \end{gather*}

Тож можна виразити швидкість руху: $$ v=\sqrt{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}gR}. $$

Відношення швидкостей до і після зміни коефіцієнта тертя тоді можна записати так: $$ \frac{v_1}{v_2}=\frac{\sqrt{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_1gR}}{\sqrt{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_2gR}} =\sqrt{\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}_2}}=\sqrt{\frac{0,72}{0,18}} =2. $$

Відповідь: 2.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Перший закон термодинаміки. Потужність.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання першого закону термодинаміки.

Дано:
\(P=2,5\ \text{кВт}\)
\(t=1\ \text{хв}\)
\(\triangle U=80\ \text{кДж}\)

Знайти:
\(\triangle E\ -\ ?\)

Теплову енергію середовища можна розрахувати за першим законом термодинаміки: $$ Q=\triangle U+A, $$ де \(\triangle U\) – зміна внутрішньої енергії середовища, \(A\) – виконана робота.

Під час роботи кондиціонера внутрішні приміщення охолоджуються тому, що тепло виводиться в середовище зовні. Тому зниження внутрішньої енергії в кімнаті на \(\triangle U\) приводить до збільшення енергії середовища на те саме \(\triangle U\).

Виконану роботу можемо обчислити, знаючи потужність кондиціонера, за формулою: \begin{gather*} P=\frac At.\\[6pt] A=Pt=2,5\ \text{кВт}\cdot 1\ \text{хв}=2500\ \text{Вт}\cdot 60\ \text{с}=150000\ \text{Дж}=150\ \text{кДж}. \end{gather*}

Тоді $$ Q=\triangle U+A=80\ \text{кДж}+150\ \text{кДж}=230\ \text{кДж}. $$

Відповідь: 230.

ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням законів для рухомих провідників у магнітному полі.

Дано:
\(l=12\ \text{м}\)
\(v=900\ \text{км/год}\)
\(B=50\ \text{мкТл}\)

Знайти:
\(\triangle \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\ -\ ?\)

Два крила літака – це один суцільний провідник, що рухається в магнітному полі. Оскільки рух літака відбувається вздовж магнітного меридіана Землі, то напрямок його швидкості збігається із горизонтальним складником напруженості магнітного поля і перпендикулярний до її вертикального складника.

Під час руху провідника перпендикулярно до ліній напруженості магнітного поля в тому самому напрямку рухаються і всі його вільні електрони. На кожен із цих вільних електронів діє сила Лоренца. За правилом лівої руки, якщо долоню повернути так, щоби чотири пальці показували напрямок, протилежний до напрямку швидкості негативно заряджених частинок, а лінії магнітної індукції входили в долоню, то великий палець лівої руки вкаже напрямок дії сили Лоренца.

У результаті цього вільні електрони змістяться в одне крило, тому крила поляризуються. Тоді для рухомого провідника в магнітному полі можна обчислити електрорушійну силу (ЕРС), що дорівнює різниці потенціалів між двома кінцями провідника: $$ \triangle \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\mathrm{EPC}=Bvl\mathrm{sin}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут між швидкістю руху провідника й напрямком ліній магнітної індукції.

Тоді

Відповідь: 0,15.

ТЕМА: Механічні коливання і хвилі. Частота й період коливань.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення параметрів коливань частинок хвилі.

Паперовий кораблик на гребені хвилі коливається так само, як і частинки води у хвилі.

Під час коливань за один період тіло повертається в початкове положення. Нехай у початковий момент часу кораблик перебуває в точці максимального відхилення рівноваги. Тоді за чверть періоду кораблик опиниться на рівні спокійної води. А за наступну чверть періоду – у точці максимального відхилення від положення рівноваги з іншого боку від рівня рівноваги, тобто в найнижчому положенні.

Якщо частота коливань \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=2\ \text{Гц}=2\ \text{с}^{-1}\), можна обчислити період коливань: $$ 1)\ T=\frac{1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}=\frac 12=0,5\ \text{с}. $$

Тоді, оскільки кораблик опиниться в найнижчій точці за половину періоду, можна обчислити цей час: $$ 2)\ t=\frac T2=0,25\ \text{с}. $$

Відповідь: 0,25.

ТЕМА: Інерціальні системи відліку. Постулати спеціальної теорії відносності.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі для тіл, що рухаються зі швидкостями, близькими до швидкості світла.

Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=2,2\ \text{мкс}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=0,8\ \text{с}\)
\(c=3\cdot 10^8\ \text{м/с}\)

1. Знайти:
\(l\ -\ ?\)

Час життя мюона на Землі можна розрахувати за формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}_0}{\sqrt{1-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}^2}{c^2}}}= \frac{2,2\ \text{мкс}}{\sqrt{1-\frac{(0,8\ \text{с})^2}{c^2}}}=\frac{2,2\ \text{мкс}}{0,6}\approx 3,67\ \text{мкс}. $$

Тоді відстань, яку мюон пройде відносно Землі, дорівнюватиме: $$ l=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=3,67\ \text{мкс}\cdot 0,8\cdot 10^8\frac{\text{м}}{\text{с}}=3,67\cdot 10^{-6}\ \text{с}\cdot 0,8\cdot 3\cdot 10^8\frac{\text{м}}{\text{с}}\approx 880\ \text{м}. $$

Відповідь: 880.