ЗНО онлайн 2019 року з фізики – додаткова сесія

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку розуміння фізичних засад рівномірного руху по колу й уміння розв’язувати розрахункові задачі на основні фізичні величини, пов’язані з рівномірним рухом по колу (доцентрове прискорення, лінійна швидкість).

Пригадаймо, що за визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.

Для правильного розв’язання задачі потрібно вибрати дві точки твердого тіла, що обертається навколо осі \(O\), і простежити за їхнім рухом (рис. 1).

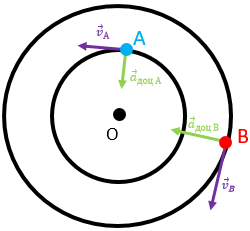
Рис. 1. Точки А і В твердого тіла

Нехай точка \(A\) лежить на відстані \(r\) від осі \(O\), а точка \(B\) на відстані \(R\) так, що \(R \gt r\). За один період обертання \(T\) всі точки повернуться у свої початкові положення. Шлях кожної точки – це коло, тож можна його обчислити як довжину цього кола: \begin{gather*} l_A=2\mathbf{\pi}r;\\[7pt] l_B=2\mathbf{\pi}r. \end{gather*}

Після цього можна обчислити лінійну швидкість кожної точки: \begin{gather*} v_A=\frac{2\mathbf{\pi}r}{T};\\[6pt] v_B=\frac{2\mathbf{\pi}r}{T}. \end{gather*}

Отже: $$ v_A \lt v_B. $$

Кутову швидкість \(\mathbf{\omega}\) точки можна обчислити за формулою: $$ \mathbf{\omega}= \frac{\mathbf{\varphi}}{t}. $$

Оскільки за період \(T\) всі точки повертаються в своє положення, то вони роблять повний (\(2\mathbf{\pi}\) радіан) оберт. А кутова швидкість для обох точок дорівнює $$ \mathbf{\omega}_{A}=\mathbf{\omega}_{B}=\frac{\mathbf{\varphi}}{t}=\frac{2\mathbf{\pi}}{T}. $$

Те саме можна зробити і для будь-якої іншої пари точок твердого тіла, отже кутова швидкість буде однаковою для всіх його точок.

Доцентрове прискорення для всіх точок напрямлене до центра, тому його напрямок відрізняється для точок у різних частинах тіла, як зображено на рисунку 1.

Модуль доцентрового прискорення можна обчислити за формулою: $$ a_{\text{доц}}=\frac{v^2}{R}. $$

Потім потрібно порівняти модулі доцентрового прискорення для точок A і B: \begin{gather*} a_{\text{доц A}}=\frac{v_A^2}{r}=\left(\frac{2\mathbf{\pi}r}{T}\right)^2 \frac 1r=r\left(\frac{2\mathbf{\pi}}{T}\right)^2;\\[6pt] a_{\text{доц B}}=\frac{v_B^2}{R}=\left(\frac{2\mathbf{\pi}R}{T}\right)^2 \frac 1R=R\left(\frac{2\mathbf{\pi}}{T}\right)^2;\\[6pt] a_{\text{доц B}} \gt a_{\text{доц A}}. \end{gather*}

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.

Завдання скеровано на оцінювання розуміння впливу сили тертя в задачах на основі побутових прикладів.

Під час перетягування каната виграє той, хто може перетягнути стрічку посередині на свій бік. Чим більшою є сила тертя між учасником і підлогою, тим більшу силу треба прикласти, щоби зсунути його з місця. Тому для здобуття перемоги тягнути канат із більшою силою ніж опонент не достатньо, якщо сила тертя з боку підлоги в нього більша.

Сила тертя з боку каната важлива, але вона не визначає переможця, адже за дуже великої сили тертя між канатом й учасником він почне рухатися разом із канатом.

Маса учасників впливає лише на те, наскільки сила тяжіння діятиме на них. Притягування Землі може піти як на користь, так і на шкоду залежно від того в який бік нахилене тіло учасника.

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.

Завдання скеровано на оцінювання розуміння закону збереження енергії в механічних процесах і розуміння поняття консервативних сил.

Закон збереження механічної енергії виконуваний лише для тих систем, у яких тіла взаємодіють тільки консервативними силами.

Консервативні сили – це сили, робота яких не залежить від форми траєкторії, а визначена лише початковим і кінцевим механічними станами тіла.

Сила тертя не є консервативною, тому для тих систем, у яких є тертя, ніколи не діє закон збереження механічної енергії.

Відповідь: B.

ТЕМА: Механіка. Кінетична й потенціальна енергія.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням поняття кінетичної енергії.

Кінетичну енергію можна визначити за формулою: $$ E_{\text{кін}}=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, \(v\) – його швидкість. Тоді нехай \(m_0\) – маса ракети на початку й \(v_0\) – початкова швидкість ракети. Тоді кінетична енергія на початку дорівнювала: $$ E_{\text{кін. поч.}}=\frac{m_0v_0^2}{2}. $$

Через деякий час маса ракети зменшилася в 3 рази, а швидкість збільшилася: \begin{gather*} m=\frac{m_0}{3};\\[6pt] v=3v. \end{gather*}

Тоді кінетична енергія дорівнюватиме: $$ E_{\text{кін}}=\frac{mv^2}{2}=\frac{m_0(3v_0)^2}{3\cdot 2}=\frac{3m_0v_0^2}{2}=3E_{\text{кін. поч.}} $$

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння стану ідеального газу. Ізопроцеси в газах.

Завдання скеровано на оцінювання розуміння закономірностей зміни тиску, об’єму й температури на основі аналізу результатів експерименту, зображених на рисунку.

За рисунком легко визначити, що об’єм кульки збільшився після того, як вона опинилася під ковпаком, до якого підключено насос. Ні охолоджувальних, ні нагрівальних пристроїв немає, тому температура газу всередині кульки залишається сталою. До того ж, оскільки кулька зав’язана, можна вважати, що кількість речовини всередині неї стала. За законом Бойля – Маріотта добуток тиску на об’єм до поміщення кульки під ковпак і після має бути однаковим: $$ p_{\text{до}}V_{\text{до}}=p_{\text{після}}V_{\text{після}}. $$

Оболонка кульки еластична, тож унаслідок наповнювання повітрям вона змінюватиме свій об’єм доти, доки тиск усередині кульки не дорівнюватиме тиску ззовні.

Тому, якщо об’єм кульки збільшився, то тиск усередині – зменшився, а отже зменшився і тиск навколо (під ковпаком).

Відповідь: A.

ТЕМА: Основи термодинаміки. Тепловий рух. Дифузія.

Завдання скеровано на оцінювання знання практичного застосування дифузії в техніці.

Дифузія – процес взаємного проникнення молекул однієї речовини між молекулами іншої внаслідок теплового руху.

Згоряння палива, плавлення льоду, тверднення рідини пов’язані з реакцією речовини на отримання або втрату теплоти, і лише під час зварювання металів вони взаємодіють.

Під час зварювання двох металів їх нагрівають на межі контактування. Тому в місці контактування метали переходять у рідкий стан. За високої температури в рідинах дифузія відбувається набагато активніше, ніж у твердих тілах за кімнатної температури. Тому атоми металів набагато легше проникають у сусідній метал, а після охолодження між ними утворюється міцний зв’язок.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Двоатомний газ кількістю речовини \(\mathbf{\nu}_0\) займає об’єм \(V\) за температури \(T_0.\) Після підвищення температури до \(T_1\), коли всі молекули розпалися на атоми, кількість речовини збільшується до \(\mathbf{\nu}_1\). Ці фізичні величини пов’язані між собою: \begin{gather*} T_1=3T_0;\\[7pt] \mathbf{\nu}_1=2\mathbf{\nu}_0. \end{gather*}

Кількість речовини збільшилась удвічі, адже кожна молекула розпалася на два атоми.

Рівняння стану ідеального газу для обох випадків: \begin{gather*} p_0V=\mathbf{\nu}_0RT_0;\\[7pt] p_1V=\mathbf{\nu}_1RT_1=2\mathbf{\nu}_0R3T_0=6\mathbf{\nu}_0RT_0. \end{gather*}

Тоді: \begin{gather*} p_0=\frac{\mathbf{\nu}_0RT_0}{V};\\[6pt] p_1=6\frac{\mathbf{\nu}_0RT_0}{V}=6p_0. \end{gather*}

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння розв’язувати задачі на аналіз графіків ізопроцесів і побудову їх у різних системах координат.

Для правильного розв’язання задачі передовсім потрібно пригадати графіки ізопроцесів (рис. 1):

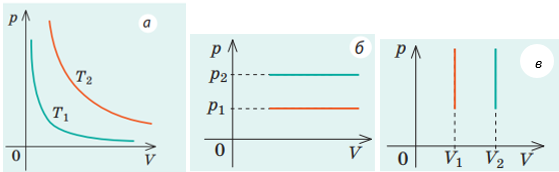
Рис. 1. Графіки ізопроцесів у координатах \((p, V)\): а) ізотермічний, б) ізобарний, в) ізохорний процеси

Важливо пам’ятати, що ізотерма може мати лише таку орієнтацію! Далі потрібно розглянути кожну послідовність із завдання і нарисувати графіки процесів.

Для правильного аналізування змін усіх фізичних величин потрібно пригадати рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. $$

Із цього випливає, що добуток тиску на об’єм, поділений на температуру залишається сталим під час переходу зі стану 1 у стан 2.

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), а отже, щоби рівність зберігалась, \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 2.

Ізобарне стискання можна зобразити прямою 2 на рисунку 2

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

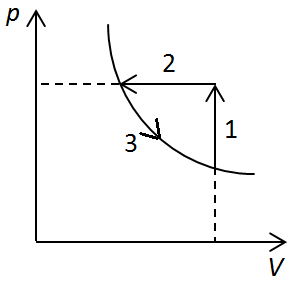
Рис. 2. Графік процесів із перебігу 1

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), тому для збереження рівності \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 3.

Ізобарне збільшення об’єму можемо зобразити прямою 2 на рисунку 3.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

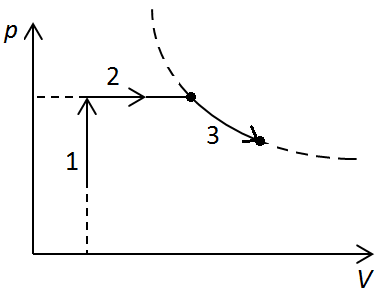
Рис. 3. Графік процесів із перебігу 2

Ізобарне стискання можна зобразити прямою 1 на рисунку 4.

Під час ізохорного охолодження за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим ніж \(p_1\), що можна зобразити прямою 2 на рисунку 4.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

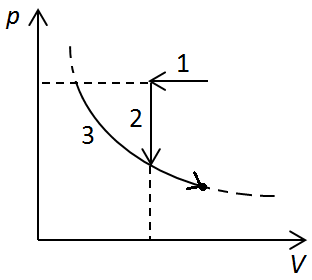
Рис. 4. Графік процесів із перебігу 3

Ізобарне збільшення об’єму можемо зобразити прямою 1 на рисунку 5.

Під час ізохорного охолодження за рівнянням Клапейрона: $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим за \(p_1\), що можна зобразити прямою 2 на рисунку 5.

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

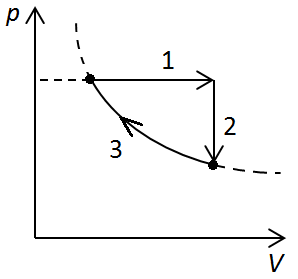
Рис. 5. Графік процесів із перебігу 4

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості рідин, газів і твердих тіл. Плавлення. Пароутворення (кипіння і випаровування).

Завдання скеровано на оцінювання вміння розв’язувати задачі на аналіз графіків теплових процесів.

За результатами аналізування графіка можна дійти висновку, що зі збільшенням отриманої кількості теплоти \(Q\) температура залишається незмінною – 0 °C (відрізок \(LM\)). Тобто 0 °C – це температура кристалізації і плавлення за атмосферного тиску. Оскільки тіло отримує додаткову теплоту, то ділянка \(LM\) відповідає плавленню.

Відрізок \(MN\) відповідає збільшенню температури від 0 °C до 100 °C зі збільшенням отриманої теплоти. Тобто ділянка \(MN\) відповідає нагріванню води, що утворилася внаслідок плавлення.

Зі збільшенням отриманої кількості теплоти \(Q\) температура залишається незмінною – 100 °C (відрізок \(NO\)). Тобто 100 °C – це температура кипіння і конденсації за атмосферного тиску, оскільки тіло отримує додаткову теплоту, то ділянка \(NO\) відповідає кипінню.

Відрізок \(OP\) відповідає збільшенню температури від 100 °C до 140 °C зі збільшенням отриманої теплоти. Тобто ділянка \(OP\) відповідає нагріванню пари, що утворилась після кипіння.

Відповідь: Г.

ТЕМА: Методи реєстрування йонізувального випромінювання.

Завдання скеровано на оцінювання розуміння принципу роботи бульбашкової камери.

Бульбашкову камеру використовують як прилад для реєстрування йонізувального випромінювання. Усередині камери міститься перегріта рідина, у якій йони, що опиняються на шляху частинки, стають центрами кипіння, тож траєкторію частинки можна визначити за бульбашками.

Для того, щоб утворити перегріту рідину, тиск усередині камери швидко зменшують. За нижчого тиску температура кипіння рідини також нижча. Температура рідини в камері не змінюється, тож рідина, що в камері, стає перегрітою.

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.

Завдання скеровано на оцінювання розуміння напруженості електричного поля і вміння порівнювати її різних точках електричного поля.

На рисунку зображено позитивний заряд \(q\), який створює навколо себе електричне поле. Щоби порівняти напруженість електричного поля в точках A і C потрібно в нього помістити пробний заряд \(Q\).

Напруженість електричного поля в точці \((\overrightarrow{E})\) – векторна фізична величина, яка характеризує електричне поле й дорівнює відношенню сили\(\overrightarrow{F}\), із якою електричне поле діє на пробний заряд, поміщений у цю точку поля, до величини цього заряду: $$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q}. $$

На пробний заряд із боку поля діє сила Кулона, яка за модулем дорівнює $$ F=k\frac{|Q||q|}{r^2}, $$ де \(r\) – відстань між зарядами, а \(k=9 \cdot 10^9\ \text{Нм}^2/\text{Кл}^2\).

Тоді модуль напруженості електричного поля дорівнюватиме $$ E=k\frac{|Q|}{r^2}. $$

Оскільки \(OA = AC\), то \(OC = OA + AC = 2OA\), а тому \begin{gather*} r_A=OA;\\[7pt] r_C=2OA=2r_A. \end{gather*}

Тоді \begin{gather*} E_A=k\frac{|Q|}{r^2_A}\\[6pt] E_C=k\frac{|Q|}{r^2C}=k\frac{|Q|}{(2r_A)^2}=k\frac{|Q|}{4r^2_A}=\frac 14 E_A. \end{gather*}

Отже $$ E_C=\frac 14 E_A $$

або $$ 4E_C=E_A $$

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження енергії зарядженого конденсатора.

Під час зарядження конденсатори набувають потенціальної енергії. Коли вони розряджаються, енергія, що накопичилась у них, розсіюється на резисторі. Розсіювання відбувається завдяки тому, що резистор нагрівається і віддає енергію в середовище. Тож резистор нагріється найбільше тоді, коли отримає найбільше енергії від конденсатора. Енергію зарядженого конденсатора обчислюють за формулою: $$ E=\frac{CU^2}{2}, $$ де \(C\) – електроємність конденсатора, а \(U\) – його робоча напруга.

Далі потрібно обчислити величини енергій чотирьох конденсаторів: \begin{gather*} E_1=\frac{C_1U_1^2}{2}=\frac{1000\ \text{мкФ}\cdot (10\ \text{В})^2}{2} =\frac{1000\cdot 10^{-6}\ \text{Ф}\cdot (10\ \text{В})^2}{2}=0,05\ \text{Дж};\\[6pt] E_2=\frac{C_2U_2^2}{2}=\frac{200\ \text{мкФ}\cdot (50\ \text{В})^2}{2} =\frac{200\cdot 10^{-6}\ \text{Ф}\cdot (50\ \text{В})^2}{2}=0,25\ \text{Дж};\\[6pt] E_3=\frac{C_3U_3^2}{2}=\frac{100\ \text{мкФ}\cdot (100\ \text{В})^2}{2} =\frac{100\cdot 10^{-6}\ \text{Ф}\cdot (100\ \text{В})^2}{2}=0,5\ \text{Дж};\\[6pt] E_4=\frac{C_4U_4^2}{2}=\frac{50\ \text{мкФ}\cdot (100\ \text{В})^2}{2} =\frac{50\cdot 10^{-6}\ \text{Ф}\cdot (100\ \text{В})^2}{2}=0,25\ \text{Дж}. \end{gather*}

Тож після підключення до третього конденсатора резистор нагріється найбільше.

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.

Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.

Нехай \(I\) – сила струму, що проходить у колі, а \(U\) – напруга в ньому. Коло складається із двох послідовних пар резисторів, що підключено паралельно. Оскільки пари резисторів з’єднано послідовно, то в кожній із них сила струму дорівнюватиме силі струму в колі: $$ I_{\text{пара 1}}=I_{\text{пара 2}}=I. $$

Напругу в колі можна обчислити як суму напруг на кожній із пар: $$ U=U_{\text{пара 1}}+U_{\text{пара 2}}. $$

Усередині кожної пари резистори з’єднано послідовно, тому сила струму в парі дорівнюватиме сумі сил струму на кожному з резисторів: \begin{gather*} I_{\text{пара 1}}=I_{R=9\ \text{Ом}}+I_{R=2\ \text{Ом}};\\[7pt] I_{\text{пара 2}}=I_{R=3\ \text{Ом}}+I_{R=8\ \text{Ом}}. \end{gather*}

Напруга на кожному резисторі дорівнює напрузі на всій парі: \begin{gather*} U_{\text{пара 1}}=U_{R=9\ \text{Ом}}=U_{R=2\ \text{Ом}};\\[7pt] U_{\text{пара 2}}=U_{R=3\ \text{Ом}}=U_{R=8\ \text{Ом}}. \end{gather*}

Опір кожної пари резисторів розраховують за правилами паралельного з’єднання провідників: \begin{gather*} \frac{1}{R_{\text{пари 1}}}=\frac{1}{R_1}+\frac{1}{R_2};\\[6pt] \frac{1}{R_{\text{пари 2}}}=\frac{1}{R_3}+\frac{1}{R_4};\\[6pt] R_{\text{пари 1}}=\frac{R_1R_2}{R_1+R_2}=\frac{9\ \text{Ом}\cdot 2\ \text{Ом}}{9\ \text{Ом}+2\ \text{Ом}}=\frac{18}{11}\ \text{Ом};\\[6pt] R_{\text{пари 2}}=\frac{R_3R_4}{R_3+R_4}=\frac{3\ \text{Ом}\cdot 8\ \text{Ом}}{3\ \text{Ом}+8\ \text{Ом}}=\frac{24}{11}\ \text{Ом}. \end{gather*}

Тоді можна за законом Ома розрахувати напругу на кожній парі: \begin{gather*} I=\frac UR;\\[6pt] U_{\text{пара 1}}=I_{\text{пара 1}}R_{\text{пари 1}}=IR_{\text{пари 1}}=\frac{18}{11}I\ (\text{В});\\[6pt] U_{\text{пара 2}}=I_{\text{пара 2}}R_{\text{пари 2}}=IR_{\text{пари 2}}=\frac{24}{11}I\ (\text{В}). \end{gather*}

Відповідь: Б, В.

ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі. Явище й закони електромагнітної індукції.

Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, пов’язані з коливальними процесами в коливальному контурі і їхнім впливом на магнітне поле, а також ваше вміння складати схеми електричного кола.

Після того, як перемикачем П конденсатор приєднують до котушки, утворюється коливальний контур. У ньому електрони, що накопичилися на одній із обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм в колі. Так конденсатор починає розряджатись.

Сила струму в котушці поступово збільшуватиметься. У котушці зі змінним струмом завжди утворюється магнітне поле. Саме воно й заряджає предмет усередині.

Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається.

Унаслідок цього процесу заряд, що був на одній обкладинці конденсатора, опинився на іншій обкладинці, тож тепер усі кроки повторяться у зворотному напрямку. У цій частині процесу струм тектиме в протилежний бік, а отже й лінії магнітної індукції також матимуть протилежний напрямок. Це почне розряджати тіло всередині.

Такі коливання заряду й енергії в коливальному контурі не можуть тривати одвічно. Частина енергії з кожним коливанням розсіюється на дротах і контактах. Тож сила струму, що проходитиме крізь котушку, щоразу буде меншою і меншою, а отже й тіло всередині перемагнічуватиметься не до кінця.

Тож коли всі коливання закінчаться, тіло, яке намагалися зарядити, матиме невеликий заряд через те, що сила струму в обох напрямках відрізнялася. Проте неможливо визначити, у якому саме напрямку буде намагнічено тіло.

Для того, щоби намагнітити тіло всередині котушки сильніше, треба примусити струм у контурі рухатися лише в одному напрямку. Тоді розмагнічування тіла не відбудеться. Пристрій, що вможливлює одностороннє пропускання струму, – це діод.

Умовні позначення для схем електричних кіл:

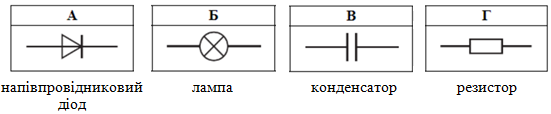
Відповідь: A.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання розуміння поняття питомого опору й механізмів проходження струму в речовинах різної природи.

Для правильного розв’язання завдання потрібно пригадати механізм перенесення заряду в кожній із речовин.

У газах струм – це газовий розряд, тобто потік вільних йонів й електронів. Для того, щоби в газах виник струм, необхідно утворити в ньому вільні йони, яких зазвичай мало. Цей процес називають йонізацією. Коли температура газу висока, то його молекули рухаються з великими швидкостями, а отже за їхніх непружних зіткнень енергії може вистачити для того, щоби примусити електрон вилетіти з атома. Тому зі збільшенням температури в газі відбувається більше зіткнень, а отже утворюється більше вільних носіїв заряду. Тому питомий опір газів збільшується зі збільшенням температури.

У металах струм – це потік вільних електронів. Зі збільшенням температури їхній рух у металі ускладняється, що пояснюють квантовою теорією електропровідності. Тому питомий опір у металах зі збільшенням температури збільшується.

В електролітах струм – це потік вільних йонів. Зі збільшенням температури кількість йонів в електролітах збільшується, а тому зменшується питомий опір.

У напівпровідниках два типи провідності – електронна (за наявності вільних електронів) і діркова (за наявності вакантних місць або дірок). Зі збільшенням температури утворюється більше вільних носіїв заряду (електронів або дірок), тому питомий опір зменшується.

Відповідь: А, В, Г.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на оцінювання розуміння природи магнітної індукції і вміння аналізувати результати експерименту за його схематичним рисунком.

Лінії індукції магнітного поля, утвореного провідником зі струмом, мають вигляд кола. Чим далі від провідника точка, тим менше в ній значення індукції магнітного поля.

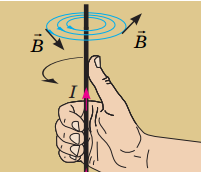
Рис. 1. Лінії магнітної індукції навколо провідника зі струмом

Коли провідник скручують у петлі, утворюється котушка. Лінії магнітної індукції всередині котушки набагато густіші (рис. 2), тож і значення індукції більше. Чим більше витків у котушці, тим більшим може бути значення індукції всередині неї.

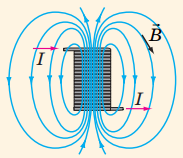
Рис. 2. Напрямок магнітної індукції в котушці

Тож, оскільки провідник поруч з усіма точками відрізняється лише тим, якої форми він набуває (петля, дві петлі чи пряма). То найбільшим буде значення індукції в центрі котушки з найбільшою кількістю петель. Тобто в точці 3.

Відповідь: B.

ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника. Пружне зіткнення.

Завдання скеровано на оцінювання розуміння поняття періоду коливань і природи пружних зіткнень.

Кулька, яку відвели на невеликий кут, перебуває на найбільшій відстані від положення рівноваги. Після того, як її відпустили, за 0,6 с вона зустрілася з другою кулькою, що була нерухомою. Тобто за 0,6 с перша кулька подолала відстань від найбільшого відхилення до положення рівноваги, тобто амплітуду. За один період тіло долає 4 амплітуди, тому період коливання цієї кульки 2,4 с.

За законом збереження імпульсу, після удару нерухому кульку також виводять із положення рівноваги, тож вона також почне коливатись. Кульку на довгій нитці, що відхиляється на невеликий кут від положення рівноваги, можна вважати математичним маятником. Період коливань математичного маятника визначають за формулою $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) – довжина математичного маятника, а \(g\) – прискорення вільного падіння.

Оскільки нитки обох маятників однакової довжини, то й період їхніх коливань буде однаковим.

Унаслідок пружного удару кульки почнуть рухатись у протилежні боки. Тоді вони одночасно почнуть рух із положення рівноваги, отже наступного разу зустрінуться, коли знову повернуться туди. Кожна з кульок пройде одну амплітуду до точки з найбільшим відхиленням, а потім ще одну – до точки рівноваги. Дві амплітуди кульки проходять за 1,2 с.

Відповідь: B.

ТЕМА: Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів. Радіолокація.

Завдання скеровано на оцінювання розуміння принципів радіолокації та вміння розв’язувати відповідні розрахункові задачі.

Радіолокатори посилають короткі імпульси в напрямку, у якому проводиться дослідження. Радіохвиля, як і інші елекромагнітні хвилі, відбивається від провідників. Тому радіохвилі відбиваються від об’єктів, які вони зустрічають на своєму шляху і повертаються до локатора. Локатор фіксує час, за який хвиля повернулась, а отже подолала дві відстані до об’єкта (від локатора до об’єкта і від об’єкта знову до локатора).

Тому відстань до об’єкта можна розрахувати за формулою $$ s=\frac{vt}{2}, $$ де \(v\) – швидкість поширення електромагнітних хвиль у середовищі, у якому здійснюють дослідження. У повітрі ця швидкість дуже близька до швидкості світла в вакуумі \(c.\)

Якщо максимальна відстань виявлення об’єкта – 150 км, можна визначити час, який знадобиться імпульсу, щоби зареєструвати сигнал від об’єкта з такої відстані: $$ t=\frac{2s}{v}=\frac{2\cdot 150\ \text{км}}{3\cdot 10^8\ \text{м}/\text{с}^2} =\frac{3\cdot 10^5\ \text{м}}{3\cdot 10^8\ \text{м}/\text{с}^2}=0,001\ \text{с}. $$

Саме з таким інтервалом радіолокатор може випускати імпульси. Тоді частота випускання імпульсів дорівнюватиме $$ v=\frac{1\ c}{t}=1000\ \text{(імпульсів)}. $$

Відповідь: A.

ТЕМА:. Оптика. Лінза. Плоске дзеркало.

Завдання скеровано на оцінювання вміння складати схеми ходу променів для розв’язання оптичних задач.

A – збиральна лінза

Б – розсіювальна лінза

В – плоске дзеркало

Г – світловод

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Квантові постулати Бора.

Завдання скеровано на оцінювання розуміння практичного застосування лінійчастих спектрів у техніці.

Лінійчасті спектри утворюються тоді, коли електрони в атомах поглинають (для спектрів поглинання) або випромінюють (для спектрів випромінювання) кванти світла. Це відбувається завдяки тому, що електрони перебувають в особливих стаціонарних станах і перехід між цими станами потребує певної кількості енергії \(h\mathbf{\nu}\), де \(\mathbf{\nu}\) – це частота кванта світла. Перехід між станами \(n\) і \(k\) описано виразом $$ h\mathbf{\nu}=|E_k-E_n|. $$

Для кожного елемента переходи можуть відбуватися лише на певних енергетичних рівнях. У результаті цих переходів утворюється унікальний набір ліній у спектрах поглинання і випромінювання, що дає змогу використати їх для визначення хімічного складу речовин.

Відповідь:Г.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання розуміння фізичних засад фотоефекту.

Заряджена цинкова пластинка розряджається внаслідок поглинання квантів світла: електрони на її поверхні отримують достатньо енергії, щоб покинути пластинку. Тож це прояв зовнішнього фотоефекту.

Пластинка розряджатиметься швидше, якщо більше електронів вилітатиме з її поверхні за одиницю часу. Що більше квантів світла потрапляє на поверхню, то більше електронів зможуть її покинути. Тобто для того, щоби збільшити швидкість розрядження пластинки, треба збільшити світловий потік.

Світло поширюється від джерела в усіх напрямках, утворюючи сферу. Тому що ближче до джерела світла знаходиться тіло, то більше фотонів потрапляє на його поверхню. Наприклад, що ближче до стіни ліхтарик, то яскравішою виглядає його світлова пляма.

Тож унаслідок зменшення відстані між ліхтарем і пластиною вона розряджатиметься швидше.

Відповідь: B.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження затримної напруги у фотоефекті.

За законами фотоефекту енергія, отримана від фотона, має бути витрачена на те, щоби вирвати електрон із поверхні катода (цю частку енергії називають роботою виходу \(A_{\text{вих}}\)), а частина енергії, яка залишається після цього, переходить у кінетичну енергію фотоелектрона \((E_{\text{кін}})\): $$ E_{\text{ф}}=A_{\text{вих}}+E_{\text{кін}} $$

Тоді, з огляду на те, що \begin{gather*} E_{\text{ф}}=3A_{\text{вих}},\\[7pt] 3A_{\text{вих}}=A_{\text{вих}}+E_{\text{кін}},\\[7pt] 2A_{\text{вих}}=E_{\text{кін}}. \end{gather*}

Під час вимірювання швидкості фотоелектронів, анод підключають до негативного полюса джерела, а катод – до позитивного. Тоді поле затримує утворені фотоелектрони. Струм не проходитиме через фотоелемент, коли робота поля дорівнюватиме кінетичній енергії найшвидших фотоелектронів: $$ A_{\text{поля}}=\mathrm{e}U_{\text{зат}}=E_{\text{кін}}, $$ де \(\mathrm{e}\) – заряд електрона, а \(U_{\text{зат}}\) – затримна напруга.

Тоді $$ U_{\text{зат}}=\frac{E_{\text{кін}}}{\mathrm{e}}=\frac{2A_{\text{вих}}}{\mathrm{e}}. $$

Відповідь: Б.

ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.

Завдання скеровано на оцінювання розуміння процесу ядерного розпаду й уміння тлумачити рівняння ядерних реакцій.

У рівняннях ядерних реакцій поруч зі знаковим символом хімічного елементом позначають лівим надрядковим індексом \(n\) кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів), а лівим підрядковим \(p\) – кількість протонів.

Схема альфа-розпаду: $$ ^{n}_{p}\mathrm{X}\ =\ ^{\mathrm{n-4}}_{\mathrm{p-2}}\mathrm{Z}\ +\ ^4_2\mathrm{He}. $$

За один альфа-розпад заряд ядра зменшуються на два елементарні заряди, а його маса зменшується на 4 а. о. м.

Схема бета-розпаду: $$ ^{n}_{p}\mathrm{X}\ =\ ^{\mathrm{\ \ \ \ n}}_{\mathrm{p+1}}\mathrm{X}\ +\ ^{\ \ \ 0}_{-1}\mathrm{e}. $$

За 1 бета-розпад заряд ядра збільшується на 1, а маса ядра не змінюється.

Тож, щоби маса ядра зменшилась на 8 а. о. м., треба, аби пройшло 2 альфа-розпади: \begin{gather*} 1)\ \ ^{n}_{p}\mathrm{X}\ =\ ^{\mathrm{n-4}}_{\mathrm{p-2}}\mathrm{Z}\ +\ ^4_2\mathrm{He};\\[7pt] 2)\ \ ^{\mathrm{n-4}}_{\mathrm{p-2}}\mathrm{Z}\ =\ ^{\mathrm{n-8}}_{\mathrm{p-4}}\mathrm{D}\ +\ ^4_2\mathrm{He}. \end{gather*}

Після двох альфа-розпадів заряд ядра зменшився на 4 елементарні заряди, а за умовою завдання заряд мав зменшитись на 3 елементарні заряди. Для цього повинен відбутися бета-розпад: $$ 3)\ \ ^{\mathrm{n-8}}_{\mathrm{p-d}}\mathrm{D}\ =\ ^{\mathrm{n-8}}_{\mathrm{p-3}}\mathrm{D}\ +\ ^{\ \ \ 0}_{-1}\mathrm{e}. $$

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.

Завдання скеровано на оцінювання розуміння кінетичної і потенціальної енергії, виконання законів збереження повної механічної енергії в механіці.

Кінетична енергія \(E\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху. Кінетичну енергію можна обчислити за формулою $$ E_{\text{кін}}=\frac{mv^2}{2}. $$

Потенціальна енергія \(U\) – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою. Потенціальну енергію тіла, що перебуває на висоті від поверхні землі, можна визначити за формулою: $$ E_{\text{пот}}=mgh, $$ де \(m\) – маса тіла, \(h\) – висота, на якій перебуває тіло.

Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхньої взаємодії.

Щодо ситуацій, описаних у завданні:

1 коли яблуко падає з гілки, висота, на якій воно перебуває, постійно зменшується, тобто зменшується його потенціальна енергія. Швидкість яблука постійно зростає. За законом збереження повної механічної енергії сума кінетичної і потенціальної енергії зберігається в системі, де діють лише консервативні сили. Тоді потенціальна енергія яблука переходить у кінетичну

2 коли м’яч летить у верхній кут воріт, його висота над землею і, відповідно, його потенціальна енергія збільшуються. Зважаючи на те, що прискорення, яке діє по вертикалі (прискорення вільного падіння), напрямлене до поверхні землі, швидкість, що напрямлена вгору, зменшується. Тому зменшується і кінетична енергія. Скориставшись законом збереження механічної енергії, можна дійти висновку, що кінетична енергія м’яча переходить у потенціальну

3 під час рівномірного падіння дощової краплі її висота, а отже й потенційна енергія, зменшується. Оскільки крапля рухається рівномірно, то її швидкість, а отже й кінетична енергія, не змінюється. Енергія не може зникнути, вона лише здатна перейти з одного виду в інший. Тож потенціальна енергія краплі переходить у її внутрішню енергію

4 під час кочення м’яча по футбольному полю висота м’яча над поверхнею землі і, відповідно, його потенціальна енергія не змінюються. Швидкість м’яча постійно зменшується внаслідок тертя. Тобто кінетична енергія м’яча переходить у внутрішню.

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.

Завдання скеровано на оцінювання розуміння понять абсолютної і відносної вологості, конденсації і точки роси.

Абсолютна вологість – фізична величина, яка характеризує вміст водяної пари в повітрі й чисельно дорівнює масі водяної пари, що міститься в повітрі об’ємом 1 м³.

Відносна вологість – фізична величина, яка показує, наскільки водяна пара близька до насичення, дорівнює відношенню абсолютної вологості до густини насиченої водяної пари за певної температури, вираженому у відсотках.

Конденсація – це перехід речовини з газуватого стану в рідкий.

Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.

Стан, за якого швидкості конденсації і пароутворення однакові, – це стан динамічної рівноваги.

Відповідь: 1Б, 2А, 3В, 4Д.

ТЕМА: Електродинаміка. Явище й закони електромагнітної індукції. Сила Ампера. Сила Лоренца.

Завдання скеровано на оцінювання знання розрахункових формул сили Ампера, сили Лоренца, індуктивності й потоку магнітної індукції.

Щодо варіантів відповіді:

A \(BS\cos\mathbf{\alpha}\), де \(B\) – магнітна індукція поля, \(S\) – площа поверхні, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і нормаллю до поверхні. Величина, що дорівнює добутку цих величин, – це потік магнітної індукції

Б \(I\triangle t\), де \(I\) – сила струму, \(\triangle t\) – проміжок часу, на якому проводили вимірювання. Добуток сили струму на проміжок часу дає змогу визначити заряд, що проходить крізь переріз провідника

B \(BIL\sin\mathbf{\alpha}\), де \(B\) – магнітна індукція поля, \(I\) – сила струму в провіднику, \(l\) – довжина провідника, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і напрямком струму. Сила, що діє на провідник зі струмом у магнітному полі, – сила Ампера, тож це вираз для модуля сили Ампера

Г \(\frac{-L\triangle I}{\triangle t}\), де \(L\) – індуктивність провідника, \(\triangle I\) – зміна сили струму, \(\triangle t\) – проміжок часу, за який відбулась зміна струму. Величина, визначена цим виразом – це ЕРС (електрорушійна сила) самоіндукції

Д \(Bvq\sin\mathbf{\alpha}\), де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки, \(\mathbf{\alpha}\) – кут між вектором магнітної індукції і напрямком руху частинки. Сила, що діє на заряджену частинку в магнітному полі – сила Ампера, тож це вираз для модуля сили Лоренца

Відповідь: 1Г, 2А, 3В, 4Д.

ТЕМА: Коливання і хвилі. Шкала електромагнітних коливань.

Завдання скеровано на оцінювання вміння визначити область застосування електромагнітних коливань певного типу.

Щодо варіантів відповіді:

1 тепло, яке ми відчуваємо від тіл навколо – це інфрачервоне випромінювання, і саме його фіксують прилади нічного бачення

2 ультрафіолетове випромінювання спричиняє опіки й пришвидшує розвиток ракових клітин. Одним з основних способів захисту людського тіла від цього випромінювання є виділення меланіну в шкірі, що може поглинути УФ-промені. Меланін – це пігмент, що відповідає за колір шкіри й очей. Що більше меланіну у шкірі, то темніша вона. Тож ультрафіолетове випромінювання є причиною засмаги

3 Рентгенівське випромінювання може бути отримане в рентгенівській трубці. Її складники – два електроди в скляній вакуумній трубці. Електрони, що вилітають з катода під дією високої напруги, потрапляють на анод, де вповільнюються. У такому разі електрони рухаються з пришвидшенням \((a \lt 0)\), а отже випромінюються електромагнітні хвилі – рентгенівське випромінювання

4 Гамма-випромінювання утворюється під час самовільного розпаду ядер атомів

Відповідь: 1Б, 2А, 3Г, 4Д.

ТЕМА: Маса. Густина. Сила Ампера.

Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, що передбачають аналіз за фотографіями результатів експерименту, пов’язаного з вагою і силою Архімеда.

1. Знайти:
\(F_A\ -\ ?\)

На рисунках схематично зображено масу, що відповідає вазі в трьох різних ситуаціях. На рисунку 1 маса, яку вимірює прилад, відповідає вазі склянки з водою: $$ P_1=m_{\text{склянки}}g=300\ \text{г}\cdot 10\ \frac{\text{м}}{\text{с}^2}=0,3\ \text{кг}\cdot 10\ \frac{\text{м}}{\text{с}^2}=3\ \text{Н}. $$

На рисунку 2 – маса, що відповідає вазі склянки з водою і бруском. Вага – це сила, із якою тіло діє на опору чи підвіс. У цьому випадку на прилад діє вага склянки з водою і сила тиску бруска. Сила тиску бруска на склянку
(і прилад відповідно) чисельно дорівнює виштовхувальній силі, що діє на брусок. Тоді вираз для ваги, якій відповідає маса на рисунку 2: $$ P_2=P_1+F_A=312\ \text{г}\cdot 10\ \frac{\text{м}}{\text{с}^2}=0,312\ \text{кг}\cdot 10\ \frac{\text{м}}{\text{с}^2}=3,12\ \text{Н}. $$

Тоді можна обчислити силу Архімеда: \begin{gather*} F_A=P_2-P_1=3,12\ \text{Н}-3\ \text{Н}=0,12\ \text{Н}. \end{gather*}

2. Знайти:
\(\mathbf{\rho}_{\text{бруска}}\ -\ ?\)

За визначенням густина дорівнює: $$ \mathbf{\rho}_{\text{бруска}} =\frac{m_{\text{бруска}}}{V_{\text{бруска}}}. $$

Силу Архімеда можна обчислити за формулою: \begin{gather*} F_A=\mathbf{\rho}gV, \end{gather*} де \(\mathbf{\rho}\) – густина рідини, у якій перебуває тіло, \(g\) – прискорення вільного падіння,
\(V\) – витіснений об’єм рідини.

Зважаючи на те, що брусок повністю занурено у воду, витіснений об’єм дорівнює об’єму бруска. Тож можна обчислити об’єм бруска: $$ V_{\text{бруска}}=V_{\text{води}}=\frac{F_A}{\mathbf{\rho}g}=\frac{0,12\ \text{Н}}{1000\ \frac{\text{кг}}{\text{м}^3}\cdot 10\ \frac{\text{м}}{\text{с}^2}}=0,000012\ \text{м}^3. $$

За вагою бруска можна обчислити його масу: \begin{gather*} P_{\text{бруска}}=F_{\text{тяж}}=m_{\text{бруска}}g;\\[7pt] m_{\text{бруска}}=\frac{F_{\text{тяж}}}{g}=\frac{0,96\ \text{Н}}{10\ \frac{\text{м}}{\text{с}^2}}=0,096\ \text{кг}. \end{gather*}

І густина бруска дорівнюватиме: $$ \mathbf{\rho}_{\text{бруска}}=\frac{m_{\text{бруска}}}{V_{\text{бруска}}}=\frac{0,096\ \text{кг}}{0,000012\ \text{м}^3}\approx 8000\ \text{кг}/\text{м}^3. $$

Відповідь: 1. 0,12. 2. 8000.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рівняння теплового балансу й коефіцієнт корисної дії (ККД).

Дано:
\(m_{\text{води}}=2\ \text{кг}\)
\(\mathbf{\tau}=10\ \text{хв}\)
\(t_1=20\ ^\circ\text{С}\)
\(t_2=100\ ^\circ\text{С}\)
\(P=2\ \text{кВт}\)
\(c_{\text{води}}=4,2\ \text{кДж}/(\text{кг}\ \cdot\ ^\circ\text{С})\)

1. Знайти:
\(Q\ -\ ?\)

Кількість теплоти, що необхідна для нагрівання цієї порції води, можемо знайти з виразу: \begin{gather*} Q=cm\triangle t=4,2\ \text{кДж}/(\text{кг}\ \cdot\ ^\circ\text{С})\cdot 2\ \text{кг}\cdot (100\ ^\circ\text{С}-20\ ^\circ\text{С})=\\[7pt] =4\ 200\ \text{Дж}/(\text{кг}\ \cdot\ ^\circ\text{С})\cdot 2\ \text{кг}\cdot 80\ ^\circ\text{С}=672\ 000\ \text{Дж}=672\ \text{кДж}, \end{gather*} де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – її маса, \(\triangle t\) – зміна температури під час охолодження.

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД можна визначити як відношення виконаної роботи \(A\) до загальної енергії \(Q\), виробленої чайником: $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}. $$

Загальну енергію, вироблену чайником, можна обчислити за формулою для його потужності: $$ P=\frac{Q}{\mathbf{\tau}}, $$ де \(Q_{\text{вит}}\) – вироблена чайником енергія, а \(\mathbf{\tau}\) – час роботи чайника.

\begin{gather*} Q_{\text{вит}}=P\mathbf{\tau}=2\ \text{кВт}\cdot 10\ \text{хв}=2\ 000\ \text{Вт}\cdot 600\ \text{с}=\\[7pt] =1\ 200\ 000\ \text{Дж}=1\ 200\ \text{кДж}. \end{gather*}

Тоді можна визначити ККД чайника: $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}=\frac{672\ \text{кДж}}{1\ 200\ \text{кДж}}\cdot 100\ \text{%}=56\ \text{%}. $$

Відповідь: 1. 672. 2. 56.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на енергію зарядженого конденсатора і її перетворення на інші види енергії.

Дано:
\(U=300\ \text{В}\)
\(C=1\ 000\ \text{мкФ}\)
\(t=1,5\ \text{мс}\)

1. Знайти:
\(E\ (\text{Дж})\ -\ ?\)

Енергію електричного поля зарядженого конденсатора можна визначити за формулою $$ E=\frac{CU^2}{2}=\frac{1\ 000\ \text{мкФ}\cdot (300\ \text{В})^2}{2}=\frac{1\ 000\cdot 10^{-6}\ \text{Ф}\cdot (300\ \text{В})^2}{2}=45\ \text{Дж}. $$

2. Знайти:
\(P\ (\text{кВт})\ -\ ?\)

Потужність спалаху \(P\) можна визначити як відношення енергії спалаху до його тривалості. Енергія спалаху – це та енергія, до якої заряджається конденсатор. \begin{gather*} P=\frac Et=\frac{45\ \text{Дж}}{1,5\ \text{мс}}=\frac{45\ \text{Дж}}{0,0015\ \text{с}}=30\ 000\ \text{Вт}=30\ \text{кВт}. \end{gather*}

Відповідь: 1. 45. 2. 30.

ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на оцінювання вміння аналізувати схеми електричного кола й розв’язувати розрахункові задачі з послідовного й паралельного підключення конденсаторів.

Дано:
\(C_1 = 0,5\ \text{мкФ}\)
\(C_2 = 1,5\ \text{мкФ}\)
\(C_3 = 2,5\ \text{мкФ}\)

1. Знайти:
\(C_{\text{заг}}\ -\ ?\)

Якщо ключ K закрити, то конденсатори \(C_2\) і \(C_3\) також будуть уключені в коло. Тоді конденсатори \(C_1,\ C_2\) і \(C_3\) будуть підключені паралельно. Ємність такої батареї конденсаторів дорівнює сумі ємностей окремих конденсаторів: $$ C_{\text{заг}}=C_1+C_2+C_3=0,5\ \text{мкФ}+1,5\ \text{мкФ}+2,5\ \text{мкФ}=4,5\ \text{мкФ}. $$

2. Знайти:
\(\frac{T_2}{T_1}\ -\ ?\)

Період коливання коливального контуру можна обчислити за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.

До того, як ключ K закрили, у коло було підключено лише конденсатор \(C_1\). Тому можна записати період електромагнітних коливань для випадків до та після закривання ключа: \begin{gather*} T_1=2\mathbf{\pi}\sqrt{LC_1};\\[7pt] T_2=2\mathbf{\pi}\sqrt{LC_{\text{заг}}}. \end{gather*}

Тоді можна розрахувати, у скільки разів збільшився період електромагнітних коливань: $$ \frac{T_2}{T_1}=\frac{2\mathbf{\pi}\sqrt{LC_{\text{заг}}}}{2\mathbf{\pi}\sqrt{LC_1}}=\frac{C_{\text{заг}}}{C_1}=\sqrt{9}=3. $$

Відповідь: 1. 4,5. 2. 3.

ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання формул рівноприскореного руху.

Дано:
\(m=1\ \text{кг}\)
\(h=10\ \text{м}\)
\(E_{\text{кін}}=10\ \text{Дж}\)

Знайти:
\(A_{\text{опору}}\ -\ ?\)

Тіло набуває максимальної кінетичної енергії тоді, коли його швидкість максимальна. Оскільки тіло падає з висоти 10 м без початкової швидкості, то воно набуде максимальної швидкості просто перед стиканням із землею. Потрібно обчислити кінетичну енергію в цей момент для випадку, коли сили опору повітря немає.

Тоді, оскільки тіло кинуто без початкової швидкості й рухається лише під дією сили тяжіння з прискоренням \(g\), можна модифікувати формулу для тіла, що рухається рівноприскорено: $$ S=V_0t+\frac{at^2}{2}\rightarrow h=\frac{>^2}{2}. $$

Далі потрібно обчислити час падіння тіла: $$ t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\cdot 10\ \text{м}}{20\ \frac{\text{м}}{\text{с}^2}}}=\sqrt{2}\ \text{с}. $$

Аналогічно для тіла, що рухається рівноприскорено: $$ V=V_0+at\rightarrow V=>. $$

Оскільки швидкість тіла, що падає, повинна постійно збільшуватись аж до моменту зіткнення з поверхнею, то можна вважати, що максимальною є швидкість за момент до падіння і використати для її розрахунку час падіння тіла: $$ V_{max}=>=10\sqrt{2}\ \frac{\text{м}}{\text{с}}. $$

Кінетичну енергію обчислюють за формулою $$ E_{\text{кін}\ max}=\frac{mv^2_{max}}{2}=\frac{1\ \text{кг}\cdot \left(10\sqrt{2}\ \frac{\text{м}}{\text{с}}\right)^2}{2}=100\ \text{Дж}. $$

Реальна кінетична енергія тіла менша, адже сила опору повітря виконує роботу проти руху тіла, тому \begin{gather*} E_{\text{кін}\ max}=A_{\text{опору}}+E_{\text{кін}},\\[7pt] A_{\text{опору}}=E_{\text{кін}\ max}-E_{\text{кін}}=100\ \text{Дж}-60\ \text{Дж}=40\ \text{Дж}. \end{gather*}

Відповідь: 40.

ТЕМА: Механіка. Основи кінематики. Середня швидкість.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані із середньою і миттєвою швидкостями тіла.

Дано:
\(v_1=20\ \frac{\text{м}}{\text{с}}\)
\(v_{\text{сер}}=24\ \frac{\text{м}}{\text{с}}\)
\(l_1=l_2\)

Знайти:
\(v_2\ -\ ?\)

Середню швидкість можна визначити за формулою: $$ v_{\text{сер}}=\frac <, $$ де \(l\) – шлях між двома містами, а \(t\) – час, за який автомобіль його подолав.

Зважаючи на те, що \begin{gather*} l=l_1+l_2,\\[7pt] t=t_1+t_2, \end{gather*} можна дійти висновку: $$ v_{\text{сер}}=\frac{l_1+l_2}{t_1+t_2}. $$

Оскільки немає інформації про час руху автомобіля на проміжку або на його половині, потрібно виразити ці величини через швидкості й шлях: \begin{gather*} t=\frac{l}{v_{\text{сер}}},\\[6pt] t=t_1+t_2=\frac{l_1}{v_1}+\frac{l_2}{v_2}. \end{gather*}

Зважаючи на те, що шлях пройдений із першою швидкістю, дорівнює шляху, пройденому з другою швидкістю, можна записати: $$ t_1+t_2=\frac{l}{2v_1}+\frac{l}{2v_2}. $$

Отже \begin{gather*} \frac{l}{v_{\text{сер}}}=\frac{l}{2v_1}+\frac{l}{2v_2};\\[6pt] \frac{l}{v_{\text{сер}}}=\frac{2v_2l+2v_1l}{4v_1v_2}=\frac{2l(v_2+v_1)}{4v_1v_2}. \end{gather*}

Тоді \begin{gather*} 4lv_1v_2=2l(v_2+v_1)v_{\text{сер}};\\[6pt] 4\cdot 20\ \frac{\text{м}}{\text{с}}\cdot v_2=2\left(v_2+20\ \frac{\text{м}}{\text{с}}\right)\cdot 24\ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2=\left(2v_2+40\ \frac{\text{м}}{\text{с}}\right)\cdot 24\ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2=48\ \frac{\text{м}}{\text{с}}\cdot v_2+960\ \frac{\text{м}}{\text{с}}\cdot \ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2-48\ \frac{\text{м}}{\text{с}}\cdot v_2=960\ \frac{\text{м}}{\text{с}}\cdot \ \frac{\text{м}}{\text{с}};\\[6pt] 32\ \frac{\text{м}}{\text{с}}\cdot v_2=960\ \frac{\text{м}}{\text{с}}\cdot\ \frac{\text{м}}{\text{с}};\\[6pt] v_2\frac{960\ \frac{\text{м}}{\text{с}}\cdot\ \frac{\text{м}}{\text{с}}}{32\ \frac{\text{м}}{\text{с}}}=30\ \frac{\text{м}}{\text{с}}. \end{gather*}

Відповідь: 30.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Дано:
\(t_1=18\ ^{\circ}\text{С}\)
\(t_2=27\ ^{\circ}\text{С}\)
\(p_1=p_2\)

Знайти:
\(\left(1-\frac{N_2}{N_1}\right)\ -\ ?\)

Температура, тиск і об’єм газу пов’язані між собою рівнянням стану ідеального газу: $$ pV=vRT, $$ де \(T\) – це температура в Кельвінах, а \(v\) – це кількість речовини, яку можна обчислити за формулою: $$ v=\frac{N}{N_A}, $$ де \(N\) – кількість молекул, \(N_A\) – число Авогадро.

Об’єм кімнати не змінився після підключення опалення, тож можна записати рівняння стану ідеального газу для стану до нагрівання і після: \begin{gather*} p_1V_1=v_1RT_1;\\[7pt] p_2V_2=v_2RT_2. \end{gather*}

Зважаючи на те, що \begin{gather*} p_1V_1=p_2V_2, \end{gather*} можна записати: \begin{gather*} v_1RT_1=v_2RT_2;\\[6pt] \frac{N_1}{N_A}RT_1=\frac{N_2}{N_A}RT_2;\\[6pt] N_1T_1=N_2T_2. \end{gather*}

Тоді $$ \frac{N_2}{N_1}=\frac{T_1}{T_2}. $$

Після цього можна обчислити, на скільки змінилася кількість молекул: $$ \left(1-\frac{N_2}{N_1}\right)\cdot 100\ \text{%}=\left(1-\frac{T_1}{T_2}\right)\cdot 100\ \text{%}=\left(1-\frac{(18+273)\ \text{К}}{(27+273)\ \text{К}}\right)\cdot 100\ \text{%}=3\ \text{%}. $$

Відповідь: 3.

ТЕМА: Магнітне поле, електромагнітна індукція. Індуктивність. Енергія магнітного поля.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані з енергією магнітного поля і її перетворенням на інші види енергії.

Дано:
\(L=2\ \text{Гн}\)
\(Q=70\ \text{Дж}\)
\(\triangle I=5\ \text{А}\)

Знайти:
\(A_{\text{стор}}\ -\ ?\)

Робота сторонніх сил акумулятора витрачається на збільшення енергії котушки. Максимальна енергія котушки може бути визначена за формулою $$ E=\frac{LI^2}{2}, $$ де \(I\) – це максимальна сила струму в котушці. За умовою задачі \(I=5\ \text{А}\).

Проте коло за умовою не ідеальне – частина роботи акумулятора втрачається у вигляді виділеної теплоти. Тоді разом робота сторонніх сил акумулятора має дорівнювати сумі енергії котушки й кількості виділеної теплоти: $$ A_{\text{стор}}=E+Q=\frac{LI^2}{2}+Q=\frac{2\ \text{Гн}\cdot (5\ \text{А})^2}{2}+70\ \text{Дж}=25\ \text{Дж}+70\ \text{Дж}=95\ \text{Дж}. $$

Відповідь: 95.

ТЕМА: Механічні коливання і хвилі. Частота й період коливань. Вимушені коливання і явище резонансу.

Завдання скеровано на оцінювання розуміння понять вимушених коливань і резонансу й уміння розв’язувати пов’язані з ними розрахункові задачі.

Дано:
\(l=1,6\ \text{м}\)

Знайти:
\(T\ -\ ?\)

Гойдалка розгойдуватиметься сильніше, якщо частота її власних коливань збігатиметься із частотою прикладання зовнішньої сили (підштовхування), тобто під час резонансу.

Оскільки між періодом і частотою існує зв’язок, який відображає формула $$ v=\frac 1t, $$ період власних коливань гойдалки має збігатися з періодом підштовхування. Період підштовхування – це і є інтервал часу між двома підштовхуваннями.

Період власних коливань гойдалки можна обчислити за виразом $$ T=2\mathbf{\pi}\sqrt{\frac lg}=2\mathbf{\pi}\sqrt{\frac{1,6\ \text{м}}{10\ \text{м/с}^2}}=2\mathbf{\pi}\sqrt{0,16\ \text{с}^2}=2\cdot 0,4\mathbf{\pi}\ \text{с}=0,8\mathbf{\pi}\ \text{с}\approx 2,5\ \text{с}. $$

А отже й інтервал між підштовхуваннями дорівнює \(2,5\ \text{с}\).

Відповідь: 2,5.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.

Дано:
\(v_{\mathbf{\alpha}}=v_p=v\)
\(m_{\mathbf{\alpha}}=4m_p\)

1. Знайти:
\(\frac{r_{\mathbf{\alpha}}}{r_p}\ -\ ?\)

Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.

Доцентрове прискорення можна обчислити з виразу $$ a_{\text{доц}}=\frac{v^2}{R}, $$ де \(v\) – швидкість частинки, а \(R\) – радіус кола, уздовж якого відбувається рух.

За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца: $$ \overrightarrow{F_{\text{Лоренца}}}=Bvq\sin\mathbf{\alpha}, $$ де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки,
\(\mathbf{\alpha}\) – кут між вектором магнітної індукції і напрямком руху частинки.

З огляду на те, що частинки рухаються в полі по колу, \(\mathbf{\alpha}=90^{\circ}\), а \(\sin\mathbf{\alpha}=1\) (рис. 1).

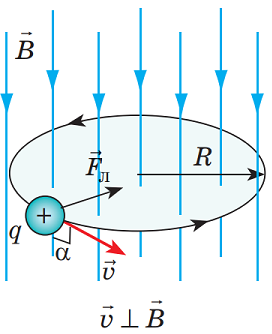
Рис. 1. Схема руху позитивно зарядженої частинки по колу

Тоді можна записати: $$ \overrightarrow{F_{\text{Лоренца}}}=m\overrightarrow{a_{\text{доц}}}. $$

Оскільки складники \(\mathbf{\alpha}\)-частинки – 2 протони й 2 нейтрони, то її заряд удвічі більший за заряд протона: $$ q_{\mathbf{\alpha}}=2q_p. $$

Запис другого закону Ньютона для обох частинок такий: \begin{gather*} \left\{ \begin{array}{l} Bv_pq_p=m_p\frac{v_p^2}{r_p};\\ Bv_{\mathbf{\alpha}}q_{\mathbf{\alpha}}=m_{\mathbf{\alpha}}\frac{v_{\mathbf{\alpha}}^2}{r_{\mathbf{\alpha}}}. \end{array} \right. \end{gather*}

Після цього потрібно записати вирази для радіусів кола, уздовж якого здійснюється рух, для обох частинок: \begin{gather*} \left\{ \begin{array}{l} r_p=m_p\frac{v_p^2}{Bv_pq_p};\\ r_{\mathbf{\alpha}}=m_{\mathbf{\alpha}}\frac{v_{\mathbf{\alpha}}^2}{Bv_{\mathbf{\alpha}}q_{\mathbf{\alpha}}}. \end{array} \right. \end{gather*}

Далі потрібно підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й \(\mathbf{\alpha}\)-частинці: \begin{gather*} \left\{ \begin{array}{l} r_p=m_p\frac{v^2}{Bvq_p};\\ r_{\mathbf{\alpha}}=4m_p\frac{v^2}{2Bvq_p}=2m_p\frac{v^2}{Bvq_p}=2r_p. \end{array} \right. \end{gather*}

Тому $$ \frac{r_{\mathbf{\alpha}}}{r_p}=2. $$

Відповідь: 2.