ЗНО онлайн 2020 року з фізики – пробний тест

ТЕМА: Фізичні явища й фізичні величини.

Завдання скеровано на оцінювання розуміння поняття фізичного явища й фізичної величини.

Фізичне явище – це зміни в природі, які можна описати за допомогою відповідних фізичних законів.

Фізична величина – це кількісно виражена характеристика тіла або фізичного явища.

Проаналізуймо поняття, наведені в кожному варіанті відповіді.

У варіанті А теплопровідність, остигання і горіння – це фізичні явища, а площа – це фізична величина.

У варіанті Б падіння, електроліз і нагрівання – це фізичні явища, а ньютон – це одиниця вимірювання сили.

У варіанті В гальмування – це фізичне явище, кілограм і діоптрія – це одиниці вимірювання маси й оптичної сили лінзи відповідно, а густина – це фізична величина.

У варіанті Г всі поняття є фізичними явищами.

Відповідь: Г.

ТЕМА: Механіка. Основи динаміки. Умови рівноваги.

Завдання скеровано на оцінювання вміння використовувати знання про умови рівноваги для розв’язування розрахункових задач.

Важіль – це тверде тіло, яке може обертатися навколо нерухомої осі – осі обертання.

Важіль перебуває в рівновазі, якщо сума моментів сил, що діють на нього, дорівнює нулю.

Момент сили \(M\) – це фізична величина, що дорівнює добутку модуля сили \(F\), яка діє на тіло, на плече \(d\) цієї сили.

Проаналізувавши рисунок до завдання, можна дійти висновку, що до лівого плеча на відстані трьох поділок прикріплено три вантажі. Кожен із цих вантажів діє на плече із силою, що дорівнює його вазі.

На праве плече важеля на відстані двох поділок діє сила, яку вимірюють динамометром.

Оскільки важіль за умовою перебуває в стані рівноваги, то \(M_1=M_2,\) де \(M_1\) i \(M_2\) – відповідні моменти сил. $$ \begin{cases} M_1=l_1P;\\ M_2=l_2F. \end{cases} $$

Вага трьох вантажів дорівнює сумі ваги кожного з них: $$ \overrightarrow{P}=m\overrightarrow{g}+m\overrightarrow{g}+m\overrightarrow{g}= 3m\overrightarrow{g} $$

На рисунку 1 позначено плечі сил \(l_1\) і \(l_2\) в умовних одиницях.

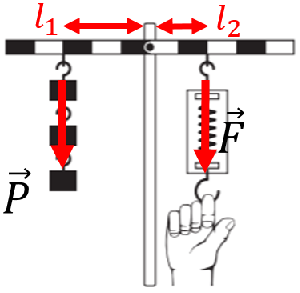
Рис. 1. Схематичний розподіл сил

$$ l_1P=l_2F, $$ тому $$ F=\frac{l_1P}{l_2}=\frac{3\cdot 3\cdot 0,1\ \text{кг}\cdot 10\frac{\text{м}}{\text{с}^2}}{2}=4,5\ \text{Н}. $$

Відповідь: Г.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.

Завдання скеровано на оцінювання розуміння понять повної механічної, кінетичної, потенціальної та внутрішньої енергії, уміння використовувати закон збереження енергії.

Механічна енергія \(E\) – це фізична величина, яка характеризує здатність тіла (системи тіл) виконати роботу.

Кінетична енергія \(T\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху.

Потенціальна енергія \(U\) – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою.

Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхніх взаємодій.

Для тіл у полі сили тяжіння (як парасольки у завданні) потенціальну енергію визначають за формулою \(U=mgh,\) де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.

На рисунку а) зображено парасольку, що лежить на підлозі, а на рисунках б) і в) – парасольки в повітрі. Висота розташування парасольок відносно землі, а отже і їхня потенціальна енергія, у всіх цих випадках різна.

Кінетичну енергію тіла можна обчислити за формулою $$ T=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, а \(v\) – швидкість його руху.

У випадку в) парасолька рухається вгору з певною швидкістю і має відмінну від нуля кінетичну енергію. Натомість парасольки на рисунках а) і б) нерухомі, їхня кінетична енергія дорівнює нулю.

Механічна енергія тіла є сумою його кінетичної і потенціальної енергій. Для всіх ситуацій, описаних у завданні, потенціальні й кінетичні енергії парасольок різні, тож і їхні суми неоднакові.

Внутрішня енергія тіла найбільше залежить від його температури й деформацій. Оскільки за умовою всі ці параметри однакові для парасольок на всіх рисунках, наведених у завданні, то й внутрішня енергія однакова для них усіх.

Відповідь: A.

ТЕМА: Сполучені посудини.

Завдання скеровано на оцінювання розуміння принципів роботи сполучених посудин.

У сполучених посудинах у кожній трубці однорідні рідини встановлюються на однаковому рівні, адже стовпчик рідини в кожній із посудин має створювати однаковий гідростатичний тиск.

Гідростатичний тиск p визначають за формулою \(p=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gh,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – густина рідини,
\(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Кристалічні тіла.

Завдання скеровано на оцінювання розуміння властивостей кристалічних тіл.

За результатами аналізування тверджень, наведених у завданнях, можна дійти висновку щодо їхньої правильності чи хибності.

1. Зберігати об’єм можуть як тверді, так і рідкі тіла. Відстань між їхніми частинками приблизно дорівнює розміру цих частинок, що сильно ускладнює стискання. Тому твердження щодо збереження об’єму кристалічного тіла правильне.

2. Зберігають форму лише тверді тіла. Таку властивість їм забезпечують кристалічні ґратки. Тому твердження щодо збереження форми кристалічного тіла правильне.

3. Перетворюються на рідину внаслідок охолодження газуваті речовини. Тому твердження щодо перетворення на рідину кристалічного тіла внаслідок його охолодження неправильне.

4. Займати весь наданий об’єм можуть лише газуваті речовини, адже відстань між їхніми частинками може бути як завгодно великою. Тому твердження, що кристалічне тіло займає весь наданий йому об’єм, неправильне.

5. Провідниками або діелектриками можуть бути як газуваті, так і рідкі чи тверді тіла. Тому твердження, що кристалічне тіло може бути провідником або діелектриком, правильне.

6. Відстань між частинками набагато більша за розмір самих частинок у газуватих речовин. Стосовно кристалічного тіла це твердження неправильне.

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Рівняння стану ідеального газу \(pV=nRT,\) де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(n\) – кількість речовини.

З огляду на це рівняння за результатами аналізування графіків, поданих у завданні, можна дійти висновків, що процес 1–2 є ізобарним (сталий тиск, температура підвищується), 2–3 є ізохорним (сталий об’єм, температура знижується), 3–4 є ізобарним (сталий тиск, температура знижується), 4–1 є ізотермічним (стала температура).

Наступним кроком є аналіз процесів, зображених у координатах \(pT.\)

Найбільших змін зазнав графік процесу 4–1, адже в координатах \(pV\) ізотерма має форму параболи, а в координатах \(pT\) – прямої, перпендикулярної до осі \(T.\)

Такому опису відповідає лише графік на рисунку A.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Внутрішня енергія і способи її зміни.

Завдання скеровано на оцінювання розуміння поняття внутрішньої енергії і способів її зміни.

Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхніх взаємодій.

Кінетична енергія руху частинок речовини й потенціальна енергію взаємодії між ними в тілі не залежить від його положення як цілого чи його швидкості.

Швидкість руху частинок речовини збільшується з підвищенням температури, а тому змінюється і внутрішня енергія всього тіла.

Тож, якщо тіло підняти на п’ять метрів, зміниться лише його потенціальна енергія. Якщо ж надати тілу швидкості, то зміниться його кінетична енергія. Якщо нагріти тіло, то збільшиться його внутрішня енергія, а якщо помістити його в теплоізолювальну шафу, то енергія тіла не зміниться.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на оцінювання вміння визначати ізопроцеси за їхнім описом і застосовувати до них перший закон термодинаміки.

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(А\) – робота, виконана тілом. Із цієї формули зрозуміло, що для того, щоби робота виконувалася лише за рахунок зменшення внутрішньої енергії, кількість теплоти, отриманої ззовні, має дорівнювати нулю \((Q=0).\) Такий процес є адіабатним.

Тож наступним кроком є аналізування ситуацій, описаних у завданні, для визначення адіабатного процесу.

А Оскільки повітря рухається швидко, то воно не встигає обмінятися теплом із навколишнім середовищем, тож \(Q=0\) і процес є адіабатним. Після цього газ розширюється і виконує роботу. За першим законом термодинаміки виконати цю роботу газ може лише за рахунок зменшення своєї внутрішньої енергії. Доказом цього є те, що водяна пара, яку несло повітря, сконденсувалася. Це є ознакою зменшення температури повітря і, відповідно, внутрішньої енергії.

Б У холодильнику відбувається обмін теплом із середовищем, отже процес не є адіабатним.

В Під час кипіння температура рідини залишається сталою, а отже і її внутрішня енергія не змінюється, що не відповідає умові завдання.

Г У цьому процесі внутрішня енергія повітря збільшується, що не відповідає умові завдання.

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.

Завдання скеровано на оцінювання знання поняття електричного заряду й розуміння принципу роботи електрометра.

Електрометр – це прилад для виявлення і вимірювання заряду. Складники електрометра – металева куля, стержні й стрілки.

У металах вільними носіями є електрони. Під дією електричного поля завжди відбувається перерозподіл зарядів. Зокрема, паличка, яку дівчинка піднесла до електрометра, утворила електричне поле, яке й стало причиною подальшого руху зарядів.

Спершу дівчинка торкнулася металевої кулі пальцем. Так вона створила шлях відходу для електронів, адже людське тіло також є хорошим провідником електричного струму.

Оскільки дівчинка до іншої частини кулі піднесла негативно заряджену паличку, то електрони, які також заряджені негативно, «відштовхнулися» від палички, перемістилися на інший бік кулі й «стекли» по руці дівчинки.

Оскільки дівчинка спершу прибрала руку, а потім паличку, то електрони не встигли повернутися назад у металеву кулю. Тому в усій конструкції електрометра виник дефіцит електронів. Унаслідок цього металевий стержень і стрілка набули позитивного заряду. Оскільки стрілка й стержень стали однойменно зарядженими, то стрілка відхилилася.

Коли дівчинка піднесла позитивно заряджену паличку до кулі, то під дією електричного поля палички знову відбувся перерозподіл зарядів. Частина електронів, зокрема зі стержня і стрілки, перемістилися ближче до палички, тому й стрілка відхилилася ще більше.

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на оцінювання вміння графічно зображувати залежності між фізичними величинами.

Залежність заряду \(q\) конденсатора від напруги \(U\) описують формулою \(q=CU,\) де \(C\) – електроємність конденсатора. Ця залежність є прямо пропорційною.

Її графік – це пряма, що проходить через початок координат.

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.

Завдання скеровано на оцінювання розуміння схематичного зображення електричного кола й уміння використовувати закон Ома для ділянки електричного кола.

Реостат – це прилад, опір якого можна змінювати. Часто опір реостата регулюють за допомогою ковзного контакту, положення якого визначає частину провідника, уключеного в коло. На схемі електричного кола чим більша частина реостата розташована після стрілки, яка показує точку включення, тим більшим є опір цього приладу (рис. 1).

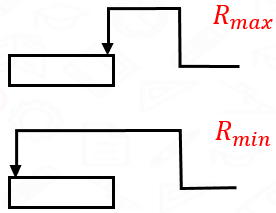
Рис. 1. Опір реостата за різних положень ковзного контакту

За умовою задачі ковзний контакт реостата перемістили в крайнє ліве положення, за рисунком це положення з мінімальним опором. Тож можна дійти висновку, що опір реостата зменшився.

Потрібно розглянути дві ситуації з відповідними показаннями амперметра, вольтметра й опором реостата – до зміни \((I_1,U_1,R_1)\) і після зміни \((I_2,U_2,R_2).\)

Реостат послідовно підключено до лампи. Сила струму в послідовно з’єднаних провідниках однакова й дорівнює загальній силі струму в ділянці кола: $$ I=I_a=I_b. $$

Загальна напруга на послідовно з’єднаних провідниках дорівнює сумі напруг на них: $$ U=U_a+U_b. $$

Загальний опір послідовно з’єднаних провідників дорівнює сумі опорів цих провідників: $$ R=R_a+R_b. $$

Позначивши загальну напругу в колі \(U,\) за законом Ома можна оцінити зміни в показах амперметра й вольтметра: $$ I=\frac UR. $$

Тож можна порівняти силу струму в двох випадках: $$ I_1=\frac{U}{R_1}\lt I_2=\frac{U}{R_2}. $$

Вольтметром у схемі вимірюють напругу на лампі. Позначивши опір лампи як \(R_{\text{л}}\) можна визначити напругу: $$ U_{\text{л}}=IR_{\text{л}}. $$

Тепер можна порівняти напругу на лампі: $$ U_1=I_1R_{\text{л}}\lt U_2=I_2R_{\text{л}}. $$

Відповідь: B.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання знання особливостей проходження струму в різних середовищах.

За результатами аналізування ситуацій, описаних у завданні, можна дійти таких висновків:

А Вільними носіями заряду в газах є електрони, позитивні й негативні йони, а не лише електрони.

Б З підвищенням температури в напівпровідниках виникають додаткові вільні носії заряду, тому питомий опір зменшується.

В Йони в металах залишаються у вузлах кристалічної ґратки й не є вільними носіями заряду, а тому не беруть участь в електропровідності.

Г В електролітах негативні йони рухаються до анода, а позитивні – до катода, а не в один бік.

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.

Завдання скеровано на оцінювання вміння визначати за правилом лівої руки напрямок сили Ампера.

Якщо ліву руку розташувати так, щоби лінії магнітної індукції входили в долоню, а чотири витягнуті пальці вказували напрямок струму в провіднику, то відігнутий на 90° великий палець укаже напрямок сили Ампера (рис. 1).

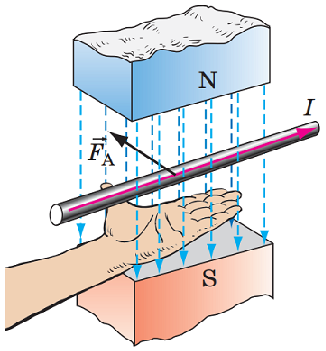
Рис. 1. Правило лівої руки

За рисунком 2 можна визначити напрямок струму I в провіднику й напрямок ліній магнітної індукції \(B\). Напрямок струму зазначено поруч із кріпленнями провідника, а напрямок ліній магнітної індукції можна визначити за таким правилом: лінії магнітної індукції беруть свій початок на північному полюсі й входять у південний. Тоді за правилом лівої руки легко визначити напрямок сили Ампера \(F_{\mathrm{A}}.\)

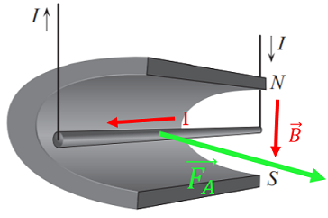
Рис. 2. Напрямок струму, ліній магнітної індукції та сили Ампера

Відповідь: A.

ТЕМА: Механічні коливання і хвилі. Частота гармонічних коливань.

Завдання скеровано на оцінювання розуміння зв’язку між частотою коливань і їхньою кількістю.

Частота коливань – це фізична величина, що дорівнює кількості коливань за одиницю часу.

За частотою \(v\) можна визначити кількість \(N\) коливань за певний проміжок часу \(t\): $$ N=vt. $$

Оскільки 1 Гц дорівнює 1 коливанню за секунду, \(N=2\ \text{c}^{-1}\cdot 10\ \text{c}=20.\)

Відповідь: Г.

ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.

Завдання скеровано на оцінювання розуміння поняття електромагнітної хвилі.

Електромагнітна хвиля – це поширення в просторі коливань електромагнітного поля.

Така хвиля – поперечна, отже коливання векторів напруженості електричного поля \(\overrightarrow{E}\) та магнітної індукції \(\overrightarrow{B}\) в ній відбуваються перпендикулярно до напрямку її поширення \(\overrightarrow{c}\) (рис. 1).

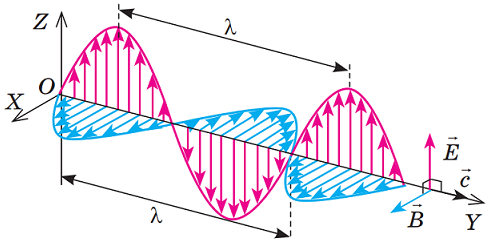
Рис. 1. Періодичні зміни вектора напруженості \(\overrightarrow{E}\) електричного поля і вектора магнітної індукції \(\overrightarrow{B}\) магнітного поля під час поширення електромагнітної хвилі в напрямку осі \(OY\)

Відповідь: Г.

ТЕМА: Коливання і хвилі.

Завдання скеровано на оцінювання знання формул для обчислення циклічної частоти коливань різної природи.

За результатами аналізування ситуацій, описаних у завданні, можна дійти таких висновків:

А Вираз містить коефіцієнт жорсткості й масу, що є характеристиками пружинного маятника.

Б Вираз містить прискорення вільного падіння і довжину, які характеризують математичний маятник.

В Вираз містить індуктивність й електроємність, які характеризують коливальний контур.

Г Вираз описує загальний зв’язок частоти й циклічної частоти коливань.

Відповідь: B.

ТЕМА: Оптика. Закони заломлення світла.

Завдання скеровано на оцінювання розуміння явища заломлення світла.

Око бачить межі різних матеріалів через те, що світло заломлюється на межі поділу середовищ.

Це одна з причин того, чому іноді складно зрозуміти чи є перед вами скло, якщо ваш погляд падає на нього перпендикулярно. Коли промінь падає на межу поділу перпендикулярно, його напрямок не змінюється.

Коли в більшій склянці стоїть менша, то промінь заломлюватиметься на межі повітря ззовні й скла зовнішньої склянки, на межі скла зовнішньої склянки й повітря між склянками, на межі повітря між склянками й скла внутрішньої склянки та на межі скла зовнішньої склянки й повітря всередині.

Коли олива заповнює порожнину меншої склянки, а згодом і порожнину між склянками, то промінь світла повинен заломлюватися стільки само разів, скільки й до заповнення. Єдине, що може «стерти» межі між склянками й оливою – це близькість їхніх показників заломлення. Якщо показники заломлення оливи й скла близькі між собою, то для світла всі ці матеріали еквівалентні еквівалентні одному суцільному шару речовини.

Відповідь: Б.

ТЕМА: Квантова фізика. Світлові кванти.

Завдання скеровано на оцінювання розуміння зв’язку між корпускулярними і хвильовими властивостями світла.

Зв’язок імпульсу фотона і його довжини хвилі описують формулою $$ p=\frac{h}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}, $$ де \(p\) – імпульс, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) – довжина хвилі фотона, \(h\) – стала Планка.

Тоді можна розрахувати модулі імпульсів обох фотонів: \begin{gather*} p_1=\frac{h}{600\cdot 10^{-9}\ \text{м}}=\frac{h}{6\cdot 10^{-7}\ \text{м}};\\[6pt] p_2=\frac{h}{60\cdot 10^{-12}\ \text{м}}=\frac{h}{6\cdot 10^{-11}\ \text{м}}=\frac{p_1}{10^{-4}};\\[6pt] p_1=10^{-4}p_2. \end{gather*}

Відповідь: Г.

ТЕМА: Квантова фізика. Атом й атомне ядро. Радіоактивність.

Завдання скеровано на оцінювання розуміння поняття «період напіврозпаду».

Період напіврозпаду \((T_{1/2})\) — це фізична величина, що характеризує радіонуклід і дорівнює часу, протягом якого розпадається половина наявної кількості ядер цього радіонукліда.

Тоді кількість ядер, що залишилася після розпаду, визначають за формулою $$ N=N_0 2^{\frac{t}{T_{1/2}}}, $$ де \(N\) – кількість ядер, що залишилась після розпаду, \(N_0\) – початкова кількість ядер, \(t\) – час розпаду.

Обчислити кількість ядер, що розпалися, можна зі співвідношення $$ N_{\text{розп}}=N_0-N=N_0-N_0 2^{\frac{t}{T_{1/2}}}. $$

Частку ядер, які розпалися, від початкової їхньої кількості, обчислюють за формулою

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Сила.

Завдання скеровано на оцінювання знання розрахункових формул сили тертя ковзання, сили Ампера, сили поверхневого натягу й сили Архімеда.

Для правильного розв’язання завдання потрібно з’ясувати фізичний зміст формул, наведених у ньому.

A \(F_A=BIl\mathrm{sin}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha},\) де \(B\) – магнітна індукція, \(I\) – сила струму в провіднику, \(l\) – довжина провідника, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут між напрямком струму й вектором магнітної індукції. Сила, що діє на провідник зі струмом у магнітному полі – сила Ампера.

Б \(F=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}l,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}\) – коефіцієнт поверхневого натягу, \(l\) – довжина лінії, що обмежує рідину. Цей вираз описує силу поверхневого натягу.

В \(F=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}N,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}\) – коефіцієнт тертя, \(N\) – сила реакції опори. Цим виразом описано силу тертя.

Г \(F=-kx,\) де \(k\) – коефіцієнт жорсткості, \(x\) – подовження тіла. Цим виразом описано силу пружності.

Д \(F=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{рідини}}gV,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{рідини}}\) − густина рідини, \(g\) – прискорення вільного падіння. Цим виразом описано силу Архімеда.

Відповідь: 1В, 2А, 3Б, 4Д.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на оцінювання розуміння процесів випаровування, кристалізації, плавлення, нагрівання і їхнього зв’язку з молекулярною будовою речовин.

1 Випаровування – це пароутворення з поверхні рідини. Під час випаровування молекули, у яких вистачає кінетичної енергії, щоби розірвати зв’язки із сусідніми молекулами, покидають поверхню рідини. А чим більша швидкість молекули, тим більша її кінетична енергія.

2 Кристалізація – це перехід речовини з рідкого стану у твердий. Основною характеристикою, що відрізняє тверді тіла від рідин – кристалічні ґратки які утворюються внаслідок переходу речовини з рідкого стану в твердий.

3 Нагрівання – це підвищення температури. Під час нагрівання речовина отримує ззовні певну кількість теплоти, яку вона витрачає на збільшення внутрішньої енергії (якщо тіло, яке нагрівають, не виконує роботи). Внутрішня енергія – це енергія взаємодії частинок тіла і їхня сумарна кінетична енергія. Чим більша внутрішня енергія, тим більша кінетична енергія частинок, а отже і їхня швидкість.

4 Плавлення – це перехід із твердого агрегатного стану в рідкий. Цей процес протилежний кристалізації, тож якщо під час кристалізації кристалічні ґратки утворюються, то під час плавлення вони руйнуються.

Відповідь: 1Д, 2Б, 3А, 4В.

ТЕМА: Одиниці фізичних величин.

Завдання скеровано на оцінювання вміння виражати одиниці фізичних величин через основні одиниці SI.

Для запису одиниць фізичних величин через основні одиниці СІ використовують метод розмірностей.

А Тесла (магнітна індукція). Потрібно вибрати формулу, із якої можна виразити магнітну індукцію через величини, одиниці яких входять у СІ або можуть бути виражені через них. Для магнітної індукції можна використати вираз для сили Ампера: $$ F_{\mathrm{A}}=BIl, $$ де \(I\) – сила струму в провіднику А, \(l\) – довжина (м) цього провідника. Із цього рівняння випливає: \begin{gather*} B=\frac{F_{\mathrm{A}}}{Il}\\[6pt] 1\ \text{Тл}=\frac{\text{Н}}{\text{А}\cdot\text{м}}=\frac{\text{кг}\cdot\text{м}}{\text{с}^2}\cdot\frac{1}{\text{А}\cdot\text{м}}. \end{gather*}

Аналогічні дії потрібно виконати й для варіантів Б – Г.

Б Генрі (індуктивність). $$ W=\frac 12 LI^2, $$ де \(W\) – енергія магнітного поля котушки (Дж), \(I\) – сила струму (А); \begin{gather*} L=\frac{2W}{I^2};\\[6pt] 1\ \text{Гн}=\frac{\text{Дж}}{\text{А}^2}=\frac{\text{кг}\cdot\text{м}^2}{\text{с}^2}\cdot\frac{1}{\text{А}^2}. \end{gather*}

B Ньютон (сила). $$ F=mg, $$ де \(m\) – маса (кг), \(g\) – прискорення вільного падіння \((\frac{\text{м}}{\text{с}^2}).\) \begin{gather*} 1\ \text{Н}=\text{кг}\cdot\frac{\text{м}}{\text{с}^2}. \end{gather*}

Г Джоуль (робота). $$ A=Fs\mathrm{cos}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(F\) – сила (Н), \(s\) – переміщення (м), \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут між напрямком переміщення і напрямком сили; \begin{gather*} 1\ \text{Дж}=\text{Н}\cdot\text{м}=\text{м}\cdot\frac{\text{кг}\cdot\text{м}}{\text{с}^2}. \end{gather*}

Відповідь: 1В, 2А, 3Д, 4Б.

ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних коливань.

Завдання скеровано на оцінювання знання галузей застосування електромагнітних коливань певного типу.

За результатами аналізування описаних у завданні ситуацій можна дійти таких висновків:

1 У ядерному реакторі відбувається радіоактивний розпад, нестабільні ядра розпадаються на стабільніші, цей розпад супроводжуваний гамма-випромінюванням.

2 Тепло, яке відчуваємо від тіл навколо – це інфрачервоне випромінювання, і саме його фіксують тепловізори.

3 Супутники зв’язку використовують радіохвилі, бо земна атмосфера найпрозоріша в цьому діапазоні, а отже інформацію можна передавати на довші відстані.

4 Люмінофор – це речовина, що випромінює видиме світло за збудження.

Відповідь: 1В, 2А, 3Г, 4Д.

ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання формул рівноприскореного руху.

1. Дано:
\(h=320\ \text{м}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

1. Знайти:
\(t\ (\text{с})-?\)

Тіло, що вільно падає, рухається лише під дією сили тяжіння. Усі тіла під час вільного падіння рухаються з однаковим прискоренням – прискоренням вільного падіння.

Рух тіла, про яке йдеться в завданні, закінчиться тоді, коли воно зустрінеться із землею, тому можна вважати, що висота падіння тіла дорівнює пройденому ним шляху.

Тіло за умовою кинуто без початкової швидкості. Тож можна скористатися модифікованою формулою для тіла, що рухається рівноприскорено: $$ s=v_0t+\frac{at^2}{2}\rightarrow\ h=\frac{gt^2}{2}. $$

Тоді час падіння тіла \begin{gather*} t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\cdot 320\ \text{м}}{10\ \frac{\text{м}}{\text{с}^2}}}=\sqrt{64\ \text{с}^2}=8\ \text{с}. \end{gather*}

2. Знайти:
\(v_{max}\ \left(\frac{\text{м}}{\text{с}}\right) - ?\)

\begin{gather*} v=v_0+at;\ \ v=gt \end{gather*}

Оскільки швидкість тіла, що падає, має постійно збільшуватись аж до моменту зіткнення з поверхнею, можна вважати, що максимальною є швидкість за момент до падіння, тому можна використати для її розрахунку час падіння тіла: \begin{gather*} v_{max}=gt=10\ \frac{\text{м}}{\text{с}^2}\cdot 8\ \text{с}=80\ \frac{\text{м}}{\text{с}}. \end{gather*}

Відповідь: 1. 8. 2. 80.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження коефіцієнта корисної дії теплової машини.

Дано:
\(A=120\ \text{кДж}\)
\(T_{\text{н}}=500\ \text{К}\)
\(T_{\text{х}}=300\ \text{К}\)

1. Знайти:
\(\text{ККД (%)}-?\)

ККД ідеальної теплової машини залежить лише від температури нагрівача й холодильника: \begin{gather*} \text{ККД}=\frac{T_{\text{н}}-T_{\text{х}}}{T_{\text{н}}}\cdot 100\ \text{%};\\[6pt] \text{ККД}=\frac{500\ \text{К}-300\ \text{К}}{500\ \text{К}}\cdot 100\ \text{%}=40\ \text{%}. \end{gather*}

2. Знайти:
\(Q_{\text{х}}\ (\text{кДж}) - ?\)

Також ККД теплової машини можна записати як відношення виконаної роботи до отриманої енергії. У цій ситуації отримана енергія – це кількість теплоти, передана нагрівачем \(Q_{\text{н}}:\) $$ \text{ККД}=\frac{A}{Q_{\text{н}}}\cdot 100\ \text{%}. $$

Теплоту, отриману від нагрівача, теплова машина використовує на виконання роботи, а залишки теплоти передає холодильнику, тому можна записати кількість теплоти, передану нагрівачем \(Q_{\text{н}}:\) $$ Q_{\text{н}}=Q_{\text{х}}+A. $$

Тоді, після підстановок,

Відповідь: 1. 40. 2. 180.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.

Завдання скеровано на оцінювання розуміння принципів роботи вольтметра й уміння розв’язувати задачі на використання закону Ома для ділянки кола.

Дано:
\(U_1=40\ \text{В}\)
\(I=10\ \text{мА}\)
\(U_2=120\ \text{В}\)

1. Знайти:
\(R_{v1}\ (\text{кОм})-?\)

За законом Ома для ділянки кола можна визначити опір вольтметра:

2. Знайти:
\(R_{\text{дод}}\ (\text{кОм})-?\)

Опір вольтметра визначає максимальну напругу, яку цим приладом можна виміряти, тому за збільшення максимальної напруги необхідно збільшувати опір вольтметра. Щоб збільшити опір вольтметра, послідовно до нього можна підключити додатковий опір.

Перш за все потрібно визначити опір вольтметра, необхідний для вимірювання напруги \(120 \ \text{В}\): $$ R_{v2}=\frac{U_2}{I}=\frac{120\ \text{В}}{0,01\ \text{А}}=12000\ \text{Ом}. $$

Можна скористатися рівністю для додавання опору послідовно з’єднаних провідників: $$ R=R_1+R_2. $$

Тоді додатковий опір, підключений до вольтметра такий:

Відповідь: 1. 4. 2. 8.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на зв’язок основних фізичних величин, що описують рівномірний рух по колу, зокрема кутової швидкості.

Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=1,57\ \frac{\text{рад}}{\text{с}}\)
\(R=20\ \text{м}\)

1. Знайти:
\(T\ (\text{с})\ -\ ?\)

Знаючи зв’язок між циклічною частотою і періодом, можна знайти період обертання: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T};\\[6pt] T=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}}=\frac{2\cdot 3,14}{1,57\ \frac{\text{рад}}{\text{с}}}=4\ \text{с}. \end{gather*}

2. Знайти::
\(l\ (\text{м})\ -\ ?\)

Період – це проміжок часу, за який тіло робить повний оберт.

Тоді за один період тіло пройде шлях, що дорівнює довжині кола, яке воно описує: $$ l=C=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R=2\cdot 3,14\cdot 20\ \text{м}=125,6\ \text{м}. $$

Відповідь: 1. 4. 2. 125,6.

ТЕМА: Вимірювання фізичних величин. Усереднення.

Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото.

Визначити середній діаметр \(\left\langle d\right\rangle\) горошин із рисунка можна, якщо загальну довжину \(l\) ланцюга горошин поділити на їхню кількість \(n\) у цьому ланцюзі. $$ \left\langle d\right\rangle=\frac ln=\frac{0,07\ \text{м}}{10}=0,007\ \text{м}=7\ \text{мм}. $$

Відповідь: 7.

ТЕМА: Механіка. Елементи механіки рідин і газів. Умова неперервності течії рідини.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання умови неперервності течії.

Дано:
\(v_{\text{ш}}=10\frac{\text{см}}{\text{с}}\)
\(d_{\text{ш}}=4d_{\text{в}}\)

Знайти:
\(v_{\text{в}}\left(\frac{\text{м}}{\text{с}}\right)\ -\ ?\)

Незалежно від зміни форми труби течія всередині повинна залишатись неперервною, тобто кількість води, що проходить за секунду через переріз труби в будь-якому місці має залишатись однаковою. Тоді чим вужча труба, тим швидшою має бути течія на цій ділянці й навпаки. Тоді умову неперервності течії для труби, у якої є дві ділянки – широка й вузька, можна записати так: $$ v_{\text{ш}}s_{\text{ш}}=v_{\text{в}}s_{\text{в}}, $$ де \(v_{\text{ш}}\) і \(v_{\text{в}}\) – це швидкості течії в широкій і вузькій частині відповідно, а \(s_{\text{ш}}\) й \(s_{\text{в}}\) – площі перерізу широкої та вузької ділянки.

Площу перерізу циліндричної труби можна обчислити за такою формулою: $$ s=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d^2}{4}. $$

Тоді \begin{gather*} v_{\text{ш}}\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d_{\text{ш}}^2}{4}=v_{\text{в}}\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d_{\text{в}}^2}{4};\\[6pt] v_{\text{в}}=v_{\text{ш}}\frac{d_{\text{ш}}^2}{d_{\text{в}}^2}=16\cdot 0,1\ \frac{\text{м}}{\text{с}}=1,6\ \frac{\text{м}}{\text{с}}. \end{gather*}

Відповідь: 1,6.

ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіл під дією кількох сил.

Дано:
\(S=10\ \text{см}^2\)
\(p_{\text{а}}=100\ \text{кПа}\)
\(p=60\ \text{кПа}\)

Знайти:
\(\overrightarrow{F}_{\text{тертя}}(\text{Н})\ -\ ?\)

Корок у пляшці – нерухомий, тому можна зробити висновок, що рівнодійна сил, які діють на нього, дорівнює нулю. Оскільки масу корка не враховують, то дією сили тяжіння можна знехтувати. Тоді на корок діють лише сила атмосферного тиску \(\overrightarrow{F}_{p\ \text{атм}}\), сила тиску повітря зсередини пляшки \(\overrightarrow{F}_p\) і сила тертя між поверхнею корка й пляшки \(\overrightarrow{F}_{\text{тертя}}\) (рис. 1).

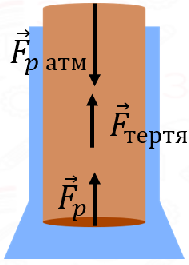
Рис. 1. Схематичне зображення сил, що діють на корок

Силу тиску можна знайти за формулою: $$ \overrightarrow{F}=pS, $$ де \(p\) – тиск, \(S\) – площа поверхні, на яку відбувається тиск.

У випадку корка, який можна вважати циліндром, площею для розрахунку обох сил тиску можна вважати площу його основи. Сила тертя діє вздовж усієї площі контакту корка з пляшкою і протидіє його руху. Оскільки атмосферний тиск більший за тиск усередині пляшки, то й сила атмосферного тиску більша, а сила тертя діятиме в тому самому напрямку, що й сила тиску повітря в пляшці.

Тепер можна спроєктувати всі сили, що діють на корок, на одну пряму й записати другий закон Ньютона для корка:

Відповідь: 40.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рівняння теплового балансу.

Дано:
\(m = 150\ \text{г}\)
\(t_1=95\ ^\circ\text{С}\)
\(Q=18,9\ \text{кДж}\)
\(c=4200\ \text{Дж/кг}\ \cdot\ ^{\circ}\text{С}\)

Знайти:
\(t_2\ (^{\circ}\text{С})\ -\ ?\)

Коли кава віддає певну кількість теплоти середовищу, вона охолоджується. Кількість відданої теплоти й зміна температури пов’язані виразом $$ Q=cm\triangle t, $$ де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – маса, \(\triangle t\) – зміна температури під час охолодження.

Зміну температури розраховують за формулою \begin{gather*} \triangle t=t_1-t_2. \end{gather*}

Тоді $$ t_2=t_1-\triangle t=t_1-\frac{Q}{cm}. $$

Після переведення значення маси з грамів у кілограми й значення кількості теплоти з кілоджоулів у джоулі можна обчислити \(t_2:\)

Відповідь: 65.

ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на дію електричного поля на заряд.

Дано:
\(q=5\ \text{нКл}\)
\(E=10\ \frac{\text{кВ}}{\text{м}}\)

Знайти:
\(F\ (\text{мкН})\ -\ ?\)

Напруженість електричного поля \(E\) – векторна фізична величина, яка характеризує електричне поле й дорівнює відношенню сили \(F,\) із якою електричне поле діє на пробний заряд, поміщений у цю точку поля, до значення \(q\) цього заряду.

Тобто $$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q}. $$

Тоді, перевівши значення заряду з нанокулонів у кулони й значення напруженості електричного поля з \(\frac{\text{кВ}}{\text{м}}\) у \(\frac{\text{В}}{\text{м}},\) можна обчислити силу:

Відповідь: 50.

ТЕМА: Робота. Потужність. ККД.

Завдання скеровано на оцінювання вміння виконувати розрахункові задачі на поняття роботи, потужності й ККД.

Дано:
\(P=3,14\ \text{кВт}\)
\(d=300\ \text{мм}\)
\(v=10\ \text{об/с}\)
\(\text{ККД}=75\ \text{%}\)

Знайти:
\(F_{\text{дії}}\ (мкН)\ -\ ?\)

ККД верстата є відношенням корисної роботи, виконаної ним, до повної роботи: $$ \text{ККД}=\frac{A_{\text{кор}}}{A_{\text{пов}}}\cdot 100\ \text{%}. $$

Корисна робота токарного верстата полягає в сточуванні шарів речовини із заготовки за рахунок сили тертя між заготовкою і різцем. Її обчислюють за формулою \(A_{\text{кор}}=Fs,\) де \(s\) – переміщення поверхні заготовки відносно різця.

Повну роботу можна розрахувати, узявши до уваги, що енергію верстат отримує від електродвигуна. Саме енергію, передану верстату двигуном, буде використано в подальшому під час роботи. Її можна визначити з виразу \(A_{\text{пов}}=Pt,\) де \(t\) – час роботи верстата.

Тоді $$ \text{ККД}=\frac{Fs}{Pt}\cdot 100\ \text{%}. $$

Переміщення поверхні заготовки відносно різця можна розрахувати, якщо вважати, що за час \(t\) заготовка робить \(N\) повних обертів: $$ N=vt. $$

Тоді за формулою довжини кола \(S=N\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d.\)

За третім законом Ньютона \(F_{\text{дії}}=F.\)

Відповідь: 0,25.

ТЕМА: Коливання і хвилі. Поперечні й поздовжні хвилі. Довжина хвилі.

Завдання скеровано на оцінювання вміння розв'язувати задачі на аналіз графічного зображення хвиль.

Довжина хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) – це відстань між двома найближчими точками, які коливаються синхронно.

Потрібно вибрати дві точки, для яких легко визначити синхронність їхнього руху, наприклад, максимуми хвилі, й обчислити відстань на ними (рис. 1).

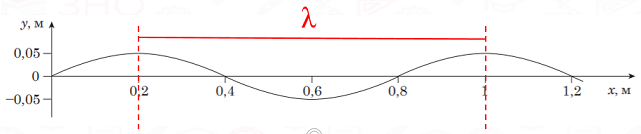
Рис. 1. Визначення довжини хвилі

Тоді $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=1\ \text{м}\ –\ 0,2\ \text{м}=0,8\ \text{м}. $$

Відповідь: 0,8.

ТЕМА: Оптика. Лінза. Формула тонкої лінзи.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на закони геометричної оптики й формулу тонкої лінзи.

Дано:
\(d_{\text{пад}}=2\ \text{см}\)
\(r_{\text{кін}}=5\ \text{см}\)
\(f=20\ \text{см}\)

Знайти:
\(F\ (\text{см})\ -\ ?\)

Спочатку потрібно намалювати схему ходу променів із завдання (рис. 1).

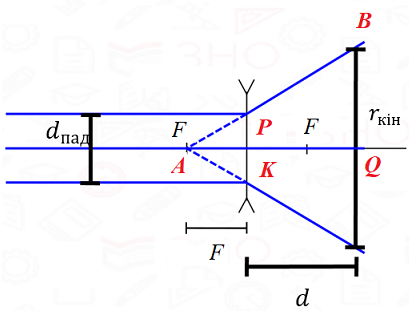
Рис. 1. Схема ходу променів

Затим необхідно перевести всі відстані з умови в одиниці СІ (метр): \begin{gather*} d_{\text{пад}}=0,02\ \text{м};\\[7pt] r_{\text{кін}}=0,05\ \text{м};\\[7pt] f=0,2\ \text{м}. \end{gather*}

Фокусну відстань можна визначити із співвідношень подібності для трикутників \(AKP\) й \(AQB:\) $$ \frac{PK}{BQ}=\frac{AK}{AQ} $$

Ці відрізки можна виразити через фізичні величини, пов’язані з ними:

Тепер можна зробити підстановку $$ \frac{d_{\text{пад}}}{2r_{\text{кін}}}=\frac{F}{F+f}=\frac{0,02\ \text{м}}{2\cdot 0,05\ \text{м}}=0,2 $$ й виразити фокусну відстань \(F\):

\begin{gather*} F=0,2(F+0,2);\\[7pt] F=0,005\ \text{м}=5\ \text{см}. \end{gather*}

Відповідь: 5.

ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії за гармонічних коливань.

Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, що передбачає оброблення й аналізування результатів експерименту, зображених на рисунку, і використання законів збереження енергії в коливальному процесі.

За рисунком 1 можна визначити довжину гумки в двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, тож його швидкість \(v\) дорівнює нулю.

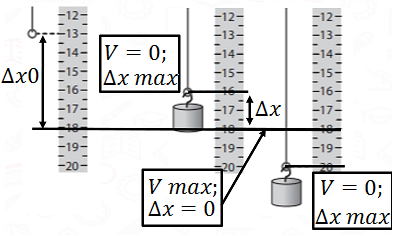
Рис. 1. Крайні положення тягарця

\begin{gather*} x_{\text{min}}=16\ \text{см};\\[7pt] x_{\text{max}}=20\ \text{см}. \end{gather*}

Також можна обчислити амплітуду коливань:

Оскільки амплітуда – це відхилення від положення рівноваги, то можна обчислити саме його. Це положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю стихнуть:

Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.

Під час коливань зберігається повна механічна енергія системи \(W\): $$ W=W_k+W_n=const, $$ де \(W_k\) – кінетична енергія, \(W_n\) – потенціальна енергія.

Кінетичну енергію визначають за формулою $$ W_k=\frac{mv^2}{2}, $$ де \(m\) – маса тіла.

Оскільки для гумової стрічки виконуваний закон Гука, то можна обчислити потенціальну енергію за формулою, що описує потенціальну енергію розтягнутої пружини: $$ W_n=\frac{k\triangle x^2}{2}, $$ де \(k\) – коефіцієнт жорсткості пружини, а \(\triangle x\) – розтяг пружини (гумової стрічки).

Хоча повна механічна енергія системи зберігається, але значення кінетичної та потенціальної енергії постійно змінюється під час коливань.

У крайніх положеннях швидкість тягарця дорівнює нулю, тож і його кінетична енергія також дорівнює нулю. А відхилення від положення рівноваги в цій ситуації найбільше, а отже й потенціальна енергія також максимальна.

У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, тож кінетична енергія приймає найбільше значення, а потенціальна стає рівною нулю.

Зважаючи на закон збереження енергії й спостереження, описані вище, можна записати рівність: \begin{gather*} W_{k\triangle x max}+W_{n\triangle x max}=W_{k\triangle x=0}+W_{n\triangle x=0};\\[7pt] W_{k max}+0=0+W_{n max};\\[7pt] W_{k max}=W_{n max};\\[6pt] \frac{mv_{max}^2}{2}=\frac{k\triangle x_{max}^2}{2}. \end{gather*}

Тоді максимальна швидкість $$ v_{max}=\sqrt{\frac{k\triangle x_{max}^2}{m}}=\sqrt{\frac km}\triangle x_{max}. $$

Відношення \(\frac km\) невідоме, але можна його визначити. У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати математичний вираз другого закону Ньютона: $$ mg=F_{\text{пр}}, $$ де \(F_{\text{пр}}\) – це сила пружності, що діє на тягарець із боку гумової стрічки. Її можна визначити за формулою $$ F_{\text{пр}}=k\triangle x_0, $$ де \(\triangle x_0\) – розтяг пружини під вагою тягарця.

$$ \triangle x_0=x_{\text{рівн}}-x_0=18\ \text{см}-13\ \text{см}=5\ \text{см}, $$ де \(x_0\) – це довжина пружини без тягарця.

Тоді $$ mg=k\triangle x_0;\ \ \frac km=\frac{g}{\triangle x_0}, $$ а

Відповідь: 28.

ТЕМА: Квантова фізика. Атом й атомне ядро. Випромінювання і поглинання світла атомом.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на енергію зв’язку атомних ядер.

Дано:
\(W_k=0,2\ \text{МеВ}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=0,495\ \text{пм}\)

Знайти:
\(E_{\text{зв}}\ (\text{МеВ})\ -\ ?\)

Атом поглинає квант, отримує від нього додаткову енергію. Ця енергія витрачається на подолання енергії зв’язку й на кінетичну енергію частинок, що утворилися після розпаду: $$ E=W_k+E_{\text{зв}}. $$

Отриману від кванта випромінювання енергію можна знайти з наступного виразу, перевівши попередньо пікометри в метри:

Оскільки сумарну кінетичну енергія в завданні зазначено в МеВ, отриманий результат також потрібно перевести в МеВ:

Тоді енергія зв’язку $$ E_{\text{зв}}=2,5\ \text{МеВ}-0,2\ \text{МеВ}=2,3\ \text{МеВ}. $$

Відповідь: 2,3.