ЗНО онлайн 2020 року з фізики – основна сесія

ТЕМА: Механіка. Кінематика. Рух тіла, кинутого горизонтально.

Завдання скеровано на перевірку розуміння закономірностей руху під діє сили тяжіння кинутого горизонтально тіла.

У тіла, кинутого горизонтально, є два складники руху – вертикальний і горизонтальний. Ці складники незалежні, тобто рух по вертикалі не впливає на рух по горизонталі.

По горизонталі точка рухається із такою самою швидкістю, що й у початковий момент часу, адже немає жодної сили, яка діє на тіло в цьому напрямку.

По вертикалі тіло рухається під дією сили тяжіння. Під дією сили тяжіння всі тіла рухаються із прискоренням вільного падіння.

Тож оскільки прискорення вздовж осі x дорівнює 0, загальне прискорення тіла збігається із прискоренням уздовж осі y, тобто прискоренням вільного падіння.

Прискорення вільного падіння завжди напрямлене перпендикулярно до поверхні Землі.

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Невагомість.

Завдання скеровано на оцінювання розуміння поняття «невагомість».

Вага \(\overrightarrow{P}\) – це сила, яка характеризує дію тіл на опору чи підвіс як наслідок гравітаційного притягання.

Невагомість – це стан тіла, за якого його вага дорівнює нулю.

У стані невагомості ні тіло не діє на опори чи підвіси навколо, ні частини тіла не діють одна на одну. Це можливо лише за умови, що на тіло діє тільки сила тяжіння. Адже вона примушує всі тіла (незалежно від їхньої маси) рухатись із тим самим прискоренням – прискоренням вільного падіння.

Також важливо пам’ятати, що маса й вага – це два різні за своєю природою поняття. Вага – це сила, а маса – міра інертності. Маса залишається однаковою незалежно від вибору системи відліку чи сил, які діють на тіло. Тож маса не може дорівнювати нулю в стані невагомості.

Відповідь: A.

ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення.

Завдання скеровано на оцінювання знання особливостей пружного зіткнення і вміння використовувати закони збереження.

Пружне зіткнення – це зіткнення, після якого сумарна кінетична енергія тіл зберігається.

За умовою завдання кулька, що рухалася зі швидкістю \(v_0\), до зіткнення мала кінетичну енергію \(W_{\text{к кульки до}}=\frac{mv_0^2}{2}\). Кінетична енергія нерухомої стіни як до, так і після зіткнення дорівнює нулю: \(W_{\text{к стіни до}}= W_{\text{к стіни після}}=0\).

Сумарна кінетична енергія до й після зіткнення в такому разі дорівнює:

Оскільки \(W_{\text{к сумарна до}}=W_{\text{к сумарна після}}\) для пружного зіткнення, то \(W_{\text{к кульки до}}=W_{\text{к кульки після}}\).

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Умови й види рівноваги.

Завдання скеровано на оцінювання розуміння поняття «рівновага».

Рівновага тіла – це збереження стану руху або стану спокою тіла з плином часу.

Тобто швидкості поступального й обертального рухів тіла в рівновазі залишаються незмінними.

Стан стійкої рівноваги – це стан, у якому за малих відхилень від положення рівноваги тіло довільно повертається в початкове положення.

Лише на рисунку Б зображено початкове положення кульки, у яке вона повертатиметься за будь-яких малих відхилень.

Відповідь: Б.

ТЕМА: Сполучені посудини.

Завдання скеровано на оцінювання розуміння поняття «гідростатичний тиск».

У сполучених посудинах у кожній трубці рівень рідин установлюється так, що гідростатичний тиск стовпчика рідини в них однаковий.

Гідростатичний тиск \((p)\) обчислюють за формулою \(p=\mathbf{\rho} gh\), де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Якщо рідини в трубках однорідні, то тиск на однаковій висоті в усіх трубках однаковий. За умовою завдання в лівій трубці посудини рівень гасу вищий за рівень води в правій трубці. Це відбувається тому, що густина гасу менша порівняно з водою, і щоби створити такий самий гідростатичний тиск, як і в стовпчика води в правій трубці, висота стовпчика гасу має бути більшою.

У точці B (див. рисунок) тиск дорівнює атмосферному \((p_a)\), а в точці A до атмосферного тиску додається тиск стовпчика гасу над рівнем цієї точки.

Тобто \(p_A\gt p_B\).

Оскільки точка C лежить на межі розділу двох рідин, то тиск стовпця гасу над нею дорівнює тиску стовпця води над точкою D на такій самій висоті, але в трубці із водою. Тож \(p_С=p_D\).

Точки E і F на однаковій висоті у воді, тому тиск у них однаковий, а \(p_E=p_F\).

Відповідь: B.

ТЕМА: Механіка. Елементи динаміки рідин і газів. Умова плавання тіл.

Завдання скеровано на оцінювання розуміння поняття «густина» і вміння застосовувати закон Архімеда.

Густина речовини \((\mathbf{\rho})\) – це фізична величина, яка характеризує речовину й дорівнює відношенню маси суцільного тіла, виготовленого із цієї речовини, до об’єму цього тіла:

Для правильного розв’язання завдання потрібно пригадати умови плавання тіл:

Густину зубної пасти, укинутої в посудину з водою, обчислюють за формулою:

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Робота в термодинаміці. Ізопроцеси.

Завдання скеровано на оцінювання розуміння поняття ізопроцесів і вміння розраховувати роботу в термодинамічних процесах.

Ізотермічний процес – змінювання стану газу деякої маси за незмінної температури.

Ізобарний процес – змінювання стану газу деякої маси за незмінного тиску.

Ізохорний процес – змінювання стану газу деякої маси за незмінного об’єму.

Адіабатний процес відбувається без теплообміну з навколишнім середовищем.

Робота в довільному термодинамічному процесі може бути обчислена як площа криволінійної трапеції під графіком залежності \(p(V)\), що відображено на рисунку 1.

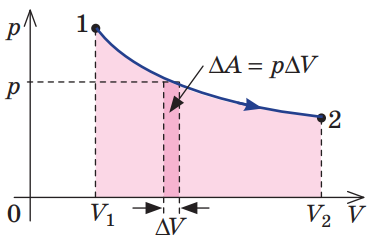
Рис. 1. Графік довільного переходу зі стану 1 у стан 2. Темнішим кольором позначено площу під криволінійною трапецією, яка дорівнює роботі

У разі ізохорного процесу об’єм не змінюється, тож площа під кривою (і робота газу) дорівнює нулю (рис. 2).

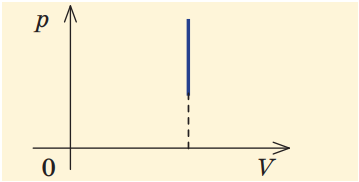
Рис. 2. Графік ізохорного процесу

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Внутрішня енергія і способи її зміни. Кількість теплоти.

Завдання скеровано на оцінювання розуміння понять внутрішньої енергії, кількості теплоти і їхнього взаємозв’язку.

За першим законом термодинаміки кількість теплоти \(Q\), передану системі, витрачено на зміну внутрішньої енергії системи \(\triangle U\) і на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=A+\triangle U $$ У процесах із незмінним об’ємом робота не виконується, тому \(A_{V=const}=0\).

Зміна внутрішньої енергії пов’язана зі зміною температури. Якщо однаково підвищити температуру двох газів однакової маси, то зміни їхньої внутрішньої енергії також будуть однаковими: $$ \triangle U_{V=const}=\triangle U_{p=const}=\triangle U. $$

За перший законом термодинаміки вирази для кількості теплоти такі:

Оскільки \(\triangle U \lt \triangle U+A_{p=const},\) то \(Q_{V=const}\lt Q_{p=const}.\)

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості рідин, газів і твердих тіл. Кристалічні тіла.

Завдання скеровано на оцінювання знання типів кристалічних речовин і їхніх властивостей.

Монокристал – тверде тіло, частинки якого утворюють суцільну кристалічну ґратку.

Полікристали – тверді тіла, які складаються з багатьох хаотично зорієнтованих маленьких кристаликів, що зрослися між собою (кристалітів).

Монокристали впорядковані в усьому своєму об’ємі. Тому за різними напрямками в таких кристалах відстані між частинками відрізняються (рис. 1). Саме ця відстань зумовлює фізичні властивості кристала, тому в монокристалах вони також залежать від напрямку. Цю властивість називають анізотропією.

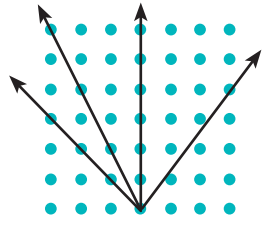
Рис. 1. Вибір напрямків у монокристалі

У полікристалах не можна вибрати напрямок крізь весь його об’єм так, щоби відстані між частинками кристалічної ґратки були незмінними, бо в кожному окремому кристаліті напрямок ґратки інший. Тому полікристали не є анізотропними.

Відповідь: Г.

ТЕМА: Електродинаміка. Явище й закони електромагнітної індукції.

Завдання скеровано на оцінювання знання поняття «електромагнітна індукція» і вміння застосовувати закони електромагнітної індукції.

Гальванометр у досліді, описаному в завданні, фіксує індукційний струм у котушці.

Для правильного розв’язання завдання потрібно пригадати закони електромагнітної індукції.

1. Електричний струм у замкненому провідному контурі виникає лише тоді, коли змінюється магнітний потік через поверхню, обмежену контуром.

2. Чим швидше змінюється магнітний потік, тим більшою є сила індукційного струму в контурі.

3. Напрямок індукційного струму в контурі залежить від того, збільшується чи зменшується магнітний потік через поверхню, обмежену контуром.

За першим законом електромагнітної індукції в котушці виникає струм, бо за наближення або введення магніту змінюється магнітний потік, що через неї протікає.

Чим швидше змінюватиметься магнітний потік, тим більшою, відповідно до другого закону електромагнітної індукції, буде сила струму. Щоби швидше змінювати магнітний потік від магніту, його треба рухати швидше.

Якщо тримати магніт нерухомо, то струм індукції в котушці не виникне, бо магнітний потік, який протікає через контур котушки, не змінюватиметься. А якщо змінити напрямок руху магніту, то, за правилом Ленца, зміниться лише напрямок індукованого струму.

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.

Завдання скеровано на оцінювання розуміння понять потенціалу й напруженості й уміння порівнювати ці величини в різних точках електричного поля.

На рисунку схематично зображено позитивний заряд, який створює навколо себе електричне поле. Для правильного розв’язання завдання потрібно позначити його величину як \(Q\), а пробний заряд \(q\) помістити в точки 1 і 2 для порівняння напруженості електричного поля і потенціалу.

Напруженість \(\overrightarrow{E}\) електричного поля в точці – векторна фізична величина, яка характеризує електричне поле й дорівнює відношенню сили \(\overrightarrow{F}\), із якою електричне поле діє на пробний заряд, поміщений у цю точку поля, до величини цього заряду. Тобто \(\overrightarrow{E}=\frac{\overrightarrow{F}}{q}\).

На пробний заряд з боку поля діє сила Кулона, модуль якої \(F=k\frac{|Q||q|}{r^2}\) , де \(r\) – відстань між зарядами, а \(k=9\cdot 10^9\ \text{Нм}^2/\text{Кл}^2\).

Тоді \(E= k\frac{|Q|}{r^2}\) – модуль напруженості електричного поля. За умовою завдання \(r_1\lt r_2\), тому \(E_1 \gt E_2\).

Потенціал \(\mathbf{\varphi}\) електростатичного поля в точці – це скалярна фізична величина, якою характеризують енергетичні властивості поля. Вона дорівнює відношенню потенціальної енергії \(W_{p}\) електричного заряду, поміщеного в цю точку поля, до величини \(q\) цього заряду: $$ \mathbf{\varphi}= \frac{W_p}{q}. $$ Потенціальну енергію взаємодії точкового заряду \(q\), поміщеного в поле, і заряду \(Q\), який є джерелом цього поля, обчислюють за формулою \(W_p=k\frac{Qq}{r},\) де \(r\) – відстань між зарядами, а \(k= 9\cdot 10^9\ \text{Нм}^2/\text{Кл}^2\). За умовою завдання \(r_1\lt r_2\), тож \(\mathbf{\varphi}_1 \gt \mathbf{\varphi}_2\).

Відповідь: A.

ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.

Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.

Яскравість світіння лампи залежить від її потужності, яку визначають за формулою \(P=UI\), де \(U\) – напруга, а \(I\) – сила струму в колі. Чим більша потужність лампи, тим більша яскравість її світіння. Тобто для правильного розв’язання задачі потрібно обчислити напругу й силу струму, який протікає через кожну з ламп.

Позначимо напругу в колі \(U,\) а опір лампочок – \(R'.\)

З рисунку зрозуміло, що лампа 1 послідовно з’єднана з лампами 2 і 3, які між собою з’єднані паралельно.

Правильне розв’язання завдання ґрунтується на розумінні законів паралельного й послідовного з’єднання провідників (див. рисунки 1–2).

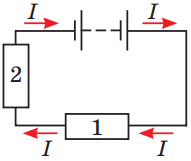
Рис. 1. Послідовне з’єднання провідників 1 і 2: \(U=U_1+U_2,\ R=R_1+R_2,\ I=I_1=I_2\)


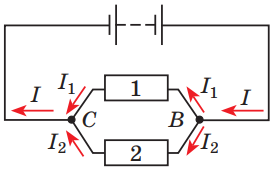
Рис. 2. Паралельне з’єднання провідників 1 і 2: \(U=U_1=U_2,\ \frac 1R=\frac{1}{R_1}+\frac{1}{R_2},\ I=I_1+I_2\)

Оскільки за умовою завдання лампи 2 і 3 з’єднані паралельно, то для цієї частини кола

Для повного кола до виходу лампи 2 з ладу

З огляду на те, що опір усіх ламп однаковий, сила струму \(I\) за законом Ома дорівнює частці від ділення напруги на опір: $$ I=\frac UR=\frac{U}{R_1+\frac{R_2 R_3}{R_2+R_3}} =\frac{2U}{3R '}. $$

Тож $$ I_1=\frac{2U}{3R '}, $$ а $$ I_3=\frac{U}{3R '}. $$ Тому на лампі 1 напруга $$ U_1=I_1 R_1=\frac{2U}{3}, $$ а на лампі 3 напруга $$ U_3=I_3 R_3=\frac U3. $$

Тобто до поломки потужність цих ламп була $$ P_{1\ до}=U_1 I_1=\frac{2U}{3}\cdot\frac{2U}{3R '} =\frac{4U^2}{9R '} $$ і $$ P_{3\ до}=U_3 I_3=\frac U3\cdot \frac{U}{3R '}=\frac{U^2}{9R '} $$ відповідно.

Після того, як лампа 2 вийшла з ладу, її опір став дуже великим, тому крізь неї струм не потече. Електричне коло після виходу з ладу лампи 2 схематично зображено на рисунку 3.

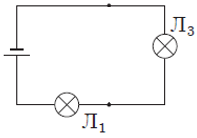
Рис. 3. Схема електричного кола після виходу з ладу лампи 2

У цьому електричному колі лампи 1 і 3 з’єднано послідовно, тому $$ U=U_1+U_3,\ R=R_1+R_3,\ I=I_1=I_3. $$

Напруга в колі не змінилася через поломку лампи, тож, за законом Ома, у цьому колі сила струму $$ I=\frac UR=\frac{U}{R_1+R_3}=\frac{U}{2R '}=I_1=I_3. $$ На кожній із ламп напруга така: $$ U_1=I_1 R_1=\frac U2,\ U_3=I_3 R_3=\frac U2. $$ Тоді після поломки їхня потужність становить

Отже, \(P_{1\ до}\gt P_{1\ після}\), а \(P_{3\ до}\lt P_{3\ після}\)

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.

Завдання скеровано на оцінювання вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.

За правилом правої руки можна визначити напрямок ліній магнітної індукції: якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом (рис. 1).

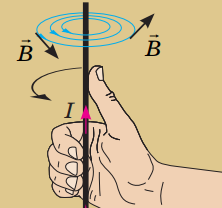
Рис. 1. Правило правої руки

Магнітна стрілка в магнітному полі повернеться вздовж ліній магнітної індукції так, що лінії входитимуть у її південний полюс і виходитимуть із її північного полюса.

Відповідь: Б.

ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на оцінювання вміння аналізувати рівняння і графік гармонічних коливань і визначати основні фізичні величини, пов’язані з ними.

Загальний вигляд рівняння гармонічних коливань \(x=A\cos(\mathbf{\omega}t+\mathbf{\varphi}_0)\) або \(x=A\sin(\mathbf{\omega}t+\mathbf{\varphi}_0)\), де \(x\) – координата, \(\mathbf{\omega}\) – циклічна частота коливань, \(\mathbf{\varphi}_0\) – початкова фаза коливань, \(t\) – час.

Обома варіантами цього рівняння можна описати будь-які гармонічні коливання, і єдине, що зміниться внаслідок переходу від рівняння, що використовує \(\sin\), до рівняння, що використовує \(\cos\), – початкова фаза.

Початкова фаза коливань – фаза коливань у момент початку відліку часу.

На рисунку до завдання в точці \(t = 0\) – максимальне відхилення від положення рівноваги. Таку криву в загальному випадку описують рівнянням

\(x=A\cos(\mathbf{\omega}t)\) або \(x=A\sin(\mathbf{\omega}t+\frac{\mathbf{\pi}}{2})\), де \(\frac{\mathbf{\pi}}{2}\) – початкова фаза.

Амплітуда коливань – це максимальне відхилення від положення рівноваги. Його можна визначити за рисунком – це відстань від осі \(x\) (рівня рівноваги) до максимуму або мінімуму синусоїди. \(A = 40\ см = 0,4\ м\).

Циклічну частоту \(\mathbf{\omega}\) визначають за формулою \(\mathbf{\omega}=\frac{\mathbf{2\pi}}{T}\), де \(T\) – період коливань (час, за який коливання повністю повторюється).

Період коливань також можна визначити за рисунком як відстань між двома максимумами синусоїди – \(T = 0,4\ с\). Тоді \(\mathbf{\omega}=\frac{2\mathbf{\pi}}{0,4}=5\mathbf{\pi}\).

Затим потрібно підставити всі визначені величини в рівняння гармонічних коливань: \(x=0,4\cos(5\mathbf{\pi}t)\) або \(x=0,4\sin(5\mathbf{\pi}t+\frac{\mathbf{\pi}}{2})\).

Відповідь: Г.

ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру і його повну енергію.

Коливальний контур – це схематично зображений на рисунку 1 фізичний пристрій із послідовно з’єднаних котушки індуктивності 1 і конденсатора 2.

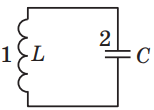
Рис. 1. Електрична схема коливального контуру

В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Якщо вважати, що в початковий момент часу конденсатор заряджений на повну, то його енергія перетікатиме в енергію котушки з максимальним струмом індукції під час коливань у такому електромагнітному контурі.

Тож можна обчислити зміну повної енергії контуру за зміною енергії зарядженого конденсатора: $$ W_{\text{конденсатора}}= \frac{q^2}{2C}, $$ де \(q\) – це максимальний заряд на обкладинці, а \(C\) – ємність конденсатора. Після збільшення максимального заряду енергія конденсатора

Відповідь: Г.

ТЕМА: Оптика. Закони заломлення світла. Відносний показник заломлення.

Завдання скеровано на оцінювання вміння визначати відносний показник заломлення речовини.

Для правильного розв’язання завдання потрібно визначити кут падіння \(\mathbf{\alpha}\) й кут заломлення \(\mathbf{\beta}\) (див. рисунок 1): \(\mathbf{\alpha}=40^{\circ},\ \mathbf{\beta}=20^{\circ}\).

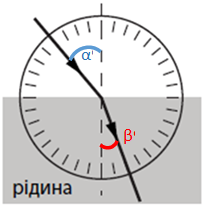
Рис. 1. Кут падіння і кут заломлення за проходження променю через межу повітря і рідини

За законом заломлення: \(n_{\text{повітря}}\sin(\mathbf{\alpha})=n_{\text{рідини}}\sin(\mathbf{\beta})\), де \(n_{\text{повітря}}\) і \(n_{\text{рідини}}\) – це відповідні абсолютні показники заломлення речовин.

Абсолютний показник заломлення \(n\) – це фізична величина, яка показує, у скільки разів швидкість поширення світла в середовищі менша порівняно з вакуумом. Його обчислюють за формулою \(n=\frac cv\), де \(c\) – швидкість світла у вакуумі, \(v\) – швидкість світла в середовищі.

За визначенням відносний показник заломлення показує, у скільки разів швидкість поширення світла в середовищі 1 більша (або менша) за швидкість поширення світла в середовищі 2.

У завданні необхідно визначити відносний показник заломлення рідини відносно повітря, тобто обчислити, у скільки разів швидкість світла в рідині менша за швидкість світла в повітрі:

За законом заломлення можна обчислити відносний показник заломлення:

Відповідь: Б.

ТЕМА: Оптика. Квантова фізика. Світлові кванти.

Завдання скеровано на оцінювання розуміння корпускулярно-хвильової природи світла і явищ інтерференції, дифракції, дисперсії і фотоефекту.

Інтерференція – явище накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.

Дифракція – явище огинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики.

Дисперсія світла – явище розкладання світла у спектр, зумовлене залежністю абсолютного показника заломлення середовища (а отже, і швидкості поширення світла в цьому середовищі) від частоти світлової хвилі.

Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.

Тобто інтерференція, дифракція і дисперсія – це явища, пов’язані з хвильовою природою світла.

Корпускулярна природа світла виявляється у фотоефекті, закони якого потрібно знати для правильного розв’язання завдання.

1. Кількість фотоелектронів, яку випромінює катод за одиницю часу, прямо пропорційна інтенсивності світла.

Цей закон фотоефекту можна пояснити й хвильовою теорією світла, адже чим більша інтенсивність світла, тим більше його частинок (фотонів) потрапляє на катод і може брати участь у взаємодії.

2. Максимальна початкова швидкість фотоелектронів збільшується зі збільшенням частоти падного світла й не залежить від його інтенсивності.

Цей закон можна пояснити, якщо розглядати фотоефект лише як явище «вибивання» фотонами електронів із поверхні катода.

Під час зіткнення у катоді з фотоном електрон поглинає енергію фотона, яку визначають за формулою \(E_ф=hv\).

Ця енергія має бути витрачена на те, щоби вирвати електрон із поверхні катода (цю частку енергії називають роботою виходу \(A_{\text{вих}}\), а та частина енергії, яка залишається після цього, переходить у кінетичну енергію фотоелектрона \((E_{\text{кін}})\): $$ E_ф=A_{\text{вих}}+E_{\text{кін}}. $$ Оскільки робота виходу залежить лише від матеріалу катода, то максимальна початкова швидкість фотоелектрона залежить від переданої фотоном енергії.
А вона залежить від частоти світла, а не від кількості фотонів, які потрапляють на катод (тобто інтенсивності).

3. Для кожної речовини є максимальна довжина світлової хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda_{\text{черв}}}\) (червона межа фотоефекту), за якої починається фотоефект.

Цей закон також пояснюють лише корпускулярною природою світла. Якщо \(hv\lt A_{\text{вих}}\), то електрони не зможуть вирватись із поверхні катода, отже існує \(ν_{min},\) за якої \(E_ф=hv_{min}=A_{\text{вих}}\), і саме це є червоною межею фотоефекту.

Відповідь: Г.

ТЕМА: Квантова фізика. Атом і атомне ядро. Альфа-, бета- й гамма-випромінювання.

Завдання скеровано на оцінювання розуміння явища бета-випромінювання.

Потік \(\mathbf{\beta}^-\)-частинок – це потік електронів, які летять зі швидкістю, близькою до швидкості світла.

Потік \(\mathbf{\beta}^+\)-частинок – це потік позитронів, які летять зі швидкістю, близькою до швидкості світла.

Потік ядер атомів Гелію називають \(\mathbf{\alpha}\)-променями, а електромагнітне випромінювання надвисокої частоти (понад \(10^{18}\) Гц) – \(\mathbf{\gamma}\)-випромінюванням.

Відповідь: Б.

ТЕМА: Квантова фізика. Атом і атомне ядро. Ядерні реакції.

Завдання скеровано на оцінювання розуміння процесу ядерного розпаду й уміння інтерпретувати рівняння ядерних реакцій.

У рівняннях ядерних реакцій біля символу хімічного елемента зліва зазначають індекси: надрядковий, що показує кількість нуклонів у ядрі (сумарну кількість протонів і нейтронів), і підрядковий – кількість протонів.

За рівнянням ядерної реакції ядро атома Алюмінію з 13 протонами й 14 нейтронами \((27 – 13 = 14)\) зіткнулося з нейтроном, у результаті чого утворився нуклід \(\mathrm{\boldsymbol{X}}\) і \(\mathbf{\alpha}\)-частинка.

Аби визначити склад ядра нукліда \(\mathrm{\boldsymbol X}\), потрібно розв’язати два рівняння – для кількості нуклонів і для кількості протонів відповідно: $$ \begin{cases} 27+1=x_1+4;\\ 13+0=x_2+2, \end{cases} $$ де \(x_1\) – це кількість нуклонів у нукліді \(\mathrm{\boldsymbol X}\), а \(x_2\) – кількість протонів у ньому.

Корені рівнянь \(x_1=24,\ x_2=11\). Отже, ідеться про нуклід \(_{11}^{24}\mathrm{\boldsymbol X}\).

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Сила.

Завдання скеровано на оцінювання розуміння природи сил пружності, поверхневого натягу, тертя і гравітаційної сили.

Для правильного розв’язання завдання потрібно розглянути кожен із проявів сил.

A. Відштовхування різнойменних електричних зарядів зумовлено їхньою кулонівською взаємодією.

Б. Амортизатори в автомобілі поглинають результати ударів від нерівностей на поверхні й забезпечують стабільне положення кузова автомобіля. Пружини амортизаторів стискаються і розтискаються під час гальмування і розгону автомобіля, можливість повернутися в попереднє положення їм забезпечує сила пружності.

В. Автомобільні покришки постійно перебувають у контакті з поверхнею. Вони мають забезпечувати тертя, адже лише так можна бути впевненим у керованості автомобіля. Проте тертя – руйнівний процес, тому із часом нерівності поверхні покришок стираються, після чого вони стають непридатними до використання. Тому це прояв саме сили тертя.

Г. Рух астероїда навколо Сонця зумовлено гравітаційним притягуванням між ними.

Д. Поверхневий шар молекул під час видування мильних бульбашок поводиться подібно до тонкої плівки (наприклад, гумової) і тому може втримувати всередині повітря. Існування такого поверхневого шару зумовлено силою поверхневого натягу.

Відповідь: 1Г, 2Б, 3Д, 4В.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія і способи її зміни. Ізопроцеси.

Завдання скеровано на оцінювання розуміння способів зміни внутрішньої енергії і вміння визначити процес, у якому відповідні зміни відбуваються.

Для правильного розв’язання завдання потрібно розглянути перетворення енергії, про які йдеться в ньому.

1. Розширення за рахунок зменшення внутрішньої енергії.

У цьому разі робота виконується за рахунок зменшення внутрішньої енергії, тобто \(A = \triangle U\).

Такий вигляд першого закону термодинаміки відповідає адіабатному процесу, адже тіло не отримує теплоти ззовні.

2. Отримана кількість теплоти витрачається на роботу і збільшення внутрішньої енергії.

Перший закон термодинаміки тоді записують як \(Q = A + \triangle U\).

Такий вигляд першого закону термодинаміки відповідає ізобарному розширенню (\(p = const,\ V\) збільшується).

3. Отримана кількість теплоти витрачається на збільшення внутрішньої енергії.

Перший закон термодинаміки записують так: \(Q = \triangle U\).

Оскільки робота не виконується, то об’єм газу не змінюється, тобто йдеться про ізохорний процес, а збільшення внутрішньої енергії передбачає нагрівання
(\(V = const,\ T\) підвищується).

4. Отримана кількість теплоти витрачається на виконання роботи.

Перший закон термодинаміки виглядає так: \(Q = A\).

Внутрішня енергія газу не змінюється, тобто процес ізотермічний. До того ж, якщо газ виконує роботу, то він розширюється (\(T = const,\ V\) збільшується).

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на оцінювання розуміння природи струму в різних середовищах.

Для правильного розв’язання завдання потрібно розглянути характерні особливості проходження струму в різних середовищах.

1. Електричний струм у розчинах і розплавах електролітів є напрямленим рухом вільних йонів (як позитивних, так і негативних).

Після того, як електроди вводять у розчин, до катода прямують позитивні йони \(\mathrm{Na}^+,\) а до анода – негативні \(\mathrm{Cl}^-\). Під час електролізу на електродах унаслідок розрядження йонів виділяються речовини: на катоді замість катіонів Натрію молекули води відновлюються до водню, а на аноді хлорид-іони окиснюються до хлору. У результаті на катоді виділяються гази: на катоді – водень, а на аноді – хлор.

2. У напівпровідниках \(n\)-типу провідність зумовлено вільними електронами, а в провідниках \(p\)-типу – переміщенням порожніх місць, у яких електронів не вистачає, тобто дірок. За яскравого освітлення фотони вибивають електрони із кристалічної ґратки напівпровідника \(n\)-типу. Ці вибиті електрони можуть ставати додатковими носіями струму, що й зменшує опір.

3. Електричний струм у металах – це напрямлений рух вільних електронів. Зі збільшенням температури електричний опір у металах зростає через те, що електрони частіше зіштовхуються із йонами кристалічної ґратки, а тому повільніше рухаються у провіднику. За наближення температури до абсолютного нуля (-273 °С) опір провідників різко зменшується майже до нуля. Таке явище називають надпровідністю.

4. Електричний струм у газах (газовий розряд) – це напрямлений рух вільних електронів, позитивних і негативних йонів. У більшості газів у нормальному стані майже немає вільних носіїв заряду, що є ознакою діелектриків. Тому необхідно якось примусити електрони відділитися від їхніх атомів і приєднатися до інших з утворенням катіонів і аніонів. Цей процес, у результаті якого гази стають провідниками, називають йонізацією. Для йонізації електронам в атомах газу потрібно надати додаткової енергії, достатньої для того, щоб покинути атом. Є багато способів надати газу цю енергію, серед яких і термічна йонізація внаслідок нагрівання газу до високих температур. За термічної йонізації молекули рухаються настільки швидко, що часто стикаються між собою. Унаслідок таких зіткнень утворюються вільні електрони і йони.

Відповідь: 1В, 2А, 3Б, 4Г.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання вміння добирати вимірювальні прилади для проведення експериментів.

A. Оскільки період – це час, за який тіло робить одне повне коливання, то для його вимірювання використовують секундомір.

Б. Для визначення електрорушійної сили (ЕРС) і внутрішнього опору джерела потрібно скористатися законом Ома для повного кола. ЕРС в цьому разі є еквівалентом напруги в законі Ома для ділянки кола, тому її також вимірюють вольтметром.

В. Для визначення фокусної відстані й оптичної сили лінзи потрібно виміряти відстань від предмета до лінзи й від лінзи до зображення. Для цього використовують лінійку.

Г. Для визначення коефіцієнта корисної дії (ККД) похилої площини необхідно обчислити корисну роботу, яку розраховують як зміну потенціальної енергії початкового й кінцевого стану й витрачену роботу, що робчислюють за формулою \(A = Fl\), де \(F\) – сила, прикладена до вантажу, а \(l\) – довжина похилої площини. Силу \(F\) у цьому досліді вимірюють динамометром.

Д. Для вивчення теплового балансу під час змішування води різної температури потрібно зафіксувати початкові й кінцеву температури. Для цього використовують термометр.

Відповідь: 1Г, 2Б, 3А, 4Д.

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі із додавання швидкостей.

1. Дано:
\(L=60\ \text{км}\)
\(t_{\text{за течією}}=3\ \text{год}\)
\(t_{\text{проти течії}}=6\ \text{год}\)

Знайти:
\(v_{\text{течії}}-?\)

Сумарна швидкість руху човна \((\overrightarrow{v}_{\text{сум}})\) є векторною сумою швидкості човна \((\overrightarrow{v}_{\text{човна}})\) і швидкості течії \((\overrightarrow{v}_{\text{течії}})\): \(\overrightarrow{v}_{\text{сум}}= \overrightarrow{v}_{\text{човна}}+\overrightarrow{v}_{\text{течії}}\) (1).

Якщо човен пливе за течією і проти неї: \(v_{\text{сум за}}= v_{\text{човна}}+v_{\text{течії}}\) (2), \(v_{\text{сум проти}}= v_{\text{човна}}-v_{\text{течії}}\) (3).

Також можна обчислити швидкості за формулами (2) і (3) з урахуванням пройденого човном шляху: \(v_{\text{сум за}}=\frac{L}{t_{\text{за течією}}}\) (4), \(v_{\text{сум проти}}=\frac{L}{t_{\text{проти течії}}}\) (5).

Підставивши (4) і (5) у (2) і (3) відповідно, можна дістати систему з двох рівнянь: \begin{gather*} \begin{cases} \frac{L}{t_{\text{за течією}}}=v_{\text{човна}}+v_{\text{течії}}\\ \frac{L}{t_{\text{проти течії}}}=v_{\text{човна}}-v_{\text{течії}} \end{cases} \ \boldsymbol (6). \end{gather*} Далі, розв’язавши систему рівнянь (6), потрібно визначити швидкість течії:

2. Знайти:
\(t_{\text{без течії}} - ?\)

Дізнатися \(t_{\text{без течії}}\) можна зі співвідношення \(v_{\text{човна}}=\frac{L}{t_{\text{без течії}}}\), із нього випливає, що \(t_{\text{без течії}}=\frac{L}{v_{\text{човна}}}\) (8).

Затим, використавши систему рівнянь (6), можна визначити \(v_{\text{човна}}\):

Тоді за формулою (8) можна обчислити \(t_{\text{без течії}}=\frac{60\ \text{км}}{15\ \text{км/год}}=4\ \text{год}\).

Відповідь: 1. 5. 2. 4.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про зв’язок частоти й амплітуди коливань із параметрами системи.

1. Дано:
\(v=300\ \text{Гц}\)
\(A=5\ \text{мм}=0,005\ \text{м}\)
\(v=8\ \text{м/с}\)

1. Знайти:
\(n_{\text{за секунду}}-?\)

\(1\ \text{Гц} = 1 с^{-1}\)

Тому 300 Гц – це 300 коливань за секунду.

2. Знайти:
\(\frac{L_{\text{крила}}}{L_{\text{бджоли}}} - ?\)

За бджолою спостерігають протягом часу \(t\).

За цей час вона зробить \(N = tn_{\text{за секунду}}\) коливань. За кожне коливання крило бджоли чотири рази проходить відстань, яка дорівнює амплітуді. Тоді $$ L_{\text{крила}}=4Atn_{\text{за секунду}}. $$

За той самий час бджола пролетить відстань \(L_{\text{бджоли}}=vt\).

Тоді

Відповідь: 1. 300. 2. 0,75.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси в газах. Робота в термодинаміці.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів.

1. Знайти:
\(A_{2-3}-?\)

За графіком на рисунку можна визначити типи процесів:

1–2 – ізобарне охолодження;

2–3 – ізохорне нагрівання.

Робота у довільному термодинамічному процесі можна обчислити як площу криволінійної трапеції під графіком залежності \(p(V).\)

Оскільки процес 2–3 – ізохорний, то \(A_{2-3}=0.\)

2. Дано:
\(V_3=12\ \text{л}\)

Знайти:
\(V_1 - ?\)

Оскільки процес 2–3 ізохорний, то \(V_3=V_2=12\ \text{л}.\)

Для процесу 1–2 за законом Гей-Люссака \(\frac{V_1}{T_1} =\frac{V_2}{T_2}\) (1), тоді \(V_1=\frac{T_1 V_2}{T_2}\) (2).

За графіком можна визначити, що \(T_1\) відповідає восьми поділкам, а \(T_2\) – двом.

Тоді \(\frac{T_1}{T_2} =\frac82=4,\) а \(V_1=4V_2=4\cdot 12\ \text{л}=48\ \text{л}.\)

Відповідь: 1. 0. 2. 48.

ТЕМА: Електродинаміка. Закон Ома для ділянки кола. Закон Ома для повного кола.

Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото й використовувати закони Ома для розв’язування розрахункових задач.

1. Знайти:
\(R_{\text{реостата}}-?\)

На рисунку A зображено вимірювання вольтметром напруги на реостаті. Оскільки між великими поділками, ціна яких 1 В, на цій шкалі нанесено п’ять малих поділок, ціна малої поділки – 0,2 В. Тоді показання вольтметра – 3,4 В.

Амперметром вимірюють силу струму в колі. Ціна великої поділки на цій шкалі 0,5 А, а між двома великими поділками нанесено десять малих поділок, тож ціна малої поділки – 0,05 А. Тому показання амперметра – 0,7 А.

Опір реостата з повзунком у положенні як на рисунку A можна обчислити за законом Ома для ділянки кола: \begin{gather*} I=\frac UR,\ \text{тож}\ R=\frac UI=\frac{3,4\ \text{В}}{0,7\ \text{Ом}}\approx 4,86\ \text{А}, \end{gather*} після округлення до одиниць – приблизно 5 А (1).

2. Знайти:
\(\mathbf{\varepsilon} - ?\)

ЕРС джерела струму \((\mathbf{\varepsilon})\) визначають за законом Ома для повного кола: \(I= \frac{\mathbf{\varepsilon}}{R+r}\), де \(R\) – опір провідників у колі, а \(r\) – внутрішній опір джерела.

Затим потрібно визначити опір реостата (див. пункт 1 цього завдання). Покази вольтметра – 3,2 В, амперметра – 0,9 А. Тоді опір реостата становить $$ R=\frac UI=\frac{3,2\ \text{В}}{0,9\ \text{А}}\approx 3,55\ \text{В}. $$ Опором вольтметра й амперметра в цьому разі можна знехтувати. ЕРС джерела і його внутрішній опір не змінилися зі зміною положення повзунка в реостаті (див. рисунки А, Б), для яких можна записати систему рівнянь $$ \begin{cases} \mathbf{\varepsilon}= I_{\text{А}} R_{\text{А}}+I_{\text{А}} r\\ \mathbf{\varepsilon}= I_{\text{Б}} R_{\text{Б}}+I_{\text{Б}} r \end{cases} \ \boldsymbol (4). $$ Далі із (4) потрібно визначити внутрішній опір джерела й скористатися (1) для спрощення виразу:

Тоді з першого рівняння в системі (4) можна визначити ЕРС:

Відповідь: 1. 5. 2. 4,1.

ТЕМА: Механіка. Умови рівноваги. Прості механізми.

Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото, і розв’язувати розрахункові задачі про рух тіла під дією однієї сили.

Знайти:
\(m-?\)

На рисунку зображено нерухомий блок. Цей простий механізм не забезпечує виграшу ні в силі, ні у відстані, а лише змінює напрямок прикладання сили.

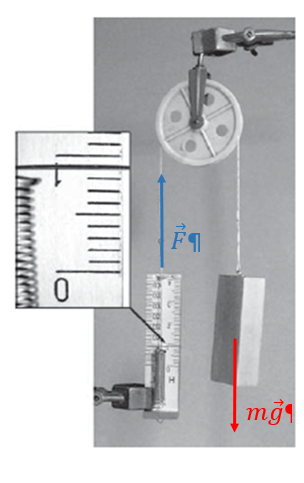
Тож сила, виміряна динамометром, – це сумарна сила, яка діє на брусок з іншого боку блоку.

На блок діє сила тяжіння \(\overrightarrow{F}_{\text{тяж}}=m\overrightarrow{g}.\)

За рисунком можна визначити силу \(\overrightarrow{F}0,9\ \text{Н}\).

Тоді $$ \overrightarrow{F}=\overrightarrow{F}_{\text{тяж}}=m\overrightarrow{g}, $$ а $$ m=\frac{\overrightarrow{F}_{\text{тяж}}}{\overrightarrow{g}}=\frac{0,9\ \text{Н}}{10\ \text{м/с}^2}=0,09\ \text{кг}=90\ \text{г}. $$

Відповідь: 90.

ТЕМА: Механіка. Основа динаміки. Додавання сил.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення рівнодійної кількох сил.

Дано:
\(F_1=3\ \text{H}\)
\(F_2=4\ \text{H}\)
\(\mathbf{\alpha}=90^\circ\)

Знайти:
\(F_{\text{рівнодійна}}-?\)

За умовою задачі схема дії сил на матеріальну точку така:

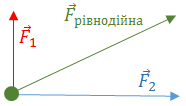
Для правильного розв’язання задачі потрібно визначити модуль рівнодійної сили, використавши теорему Піфагора й правило додавання векторів: $$ F_{\text{рівнодійна}}=\sqrt{F_1^2+F_2^2}=\sqrt{3^2+4^2}=5\ \text{H}. $$

Відповідь: 5.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рівняння теплового балансу.

Дано:
\(t_{\text{холодна}}=10\ ^\circ \mathrm{C}\)
\(V_{\text{холодна}}=100\ \text{мл}=0,0001\ \text{м}^3\)
\(t_{\text{гаряча}}=90\ ^\circ \mathrm{C}\)
\(V_{\text{гаряча}}=300\ \text{мл}=0,0003\ \text{м}^3\)

Знайти:
\(t_{\text{суміш}}-?\)

Для правильного розв’язання завдання потрібно записати вираз для суміші рідин різної температури:

Масу води обчислюють за її об’ємом і густиною: $$ m=\mathbf{\rho}V\ \boldsymbol (2). $$ Потім потрібно підставити (2) в (1) і скоротити:

Тоді

Відповідь: 70.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на відносну вологість повітря.

Дано:
\(\mathbf{\varphi} = 60\text{%}\)
\(\mathbf{\rho}_{\text{нас. пари}}=20\ \text{г/м}^3\)
\(V=50\ \text{м}^3\)

Знайти:
\(m_{\text{пари}}-?\)

Спочатку потрібно обчислити масу водяної пари в повітрі об’ємом \(1\ \text{м}^3\), тобто абсолютну вологість \(\mathbf{\rho}_a\): $$ \mathbf{\varphi}=\frac{\mathbf{\rho}_a}{\mathbf{\rho}_{\text{нас. пари}}}\cdot 100\text{%}. $$ Тоді

Маса водяної пари в кімнаті \begin{gather*} m_{\text{пари}}=\mathbf{\rho}_a V=12\ \text{г/м}^3\cdot 50\ \text{м}^3=600\ \text{г}. \end{gather*}

Відповідь: 600.

ТЕМА: Електродинаміка. Електричний струм.

Завдання скеровано на оцінювання розуміння поняття електричного струму.

Дано:
\(N=3\cdot 10^{21}\)
\(\overrightarrow{e}=1,6\cdot 10^{-19}\ \text{Кл}\)
\(t=1\ \text{хв}=60\ \text{c}\)

Знайти:
\(I-?\)

Сила струму – це фізична величина, яка характеризує електричний струм і чисельно дорівнює заряду, що за секунду проходить через поперечний переріз провідника: $$ I=\frac qt $$ За час \(t\) сумарний заряд \(q\) дорівнюватиме заряду всіх електронів, що проходять через переріз провідника, тобто \(q=N\overrightarrow{e}.\) Тоді \begin{gather*} I=\frac{N\overrightarrow{e}}{t}=\frac{3\cdot 10^{21}\cdot 1,6\cdot 10^{-19}\ \text{Кл}}{60\ \text{c}}=8\ \text{A}. \end{gather*}

Відповідь: 8.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.

Завдання скеровано на оцінювання вміння обчислювати енергію магнітного поля провідника зі струмом.

Дано:
\(I=20\ \text{А}\)
\(B=0,5\ \text{Вб}\)

Знайти:
\(W_{\text{котушки}}-?\)

Для визначення енергії магнітного поля котушки потрібно скористатися формулою \(W_{\text{котушки}}=\frac{LI^2}{2}\) (1), де \(L\) – індуктивність котушки, а \(I\) – сила струму, що тече в цій котушці. При цьому магнітний потік \(\mathbf{\Phi}\) крізь котушку пропорційний силі струму, що через неї протікає: $$ \mathbf{\Phi}=LI\ \boldsymbol (2). $$ Виразивши з (2) індуктивність і підставивши її в (1), можна дістати:

Відповідь: 5.

ТЕМА: Механіка. Кінематика. Рух тіла, кинутого горизонтально.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на характеристики коливального контуру.

Дано:
\(\triangle I=1,2\ \text{А}\)
\(\triangle t=0,6\ \text{c}\)
\(\mathbf{\varepsilon}_{\text{с.і.}}=0,2\ \text{мВ}=0,0002\ \text{В}\)
\(C=0,2\ \text{пФ}=10\cdot 10^{-12}\ \text{Ф}=10^{-11}\ \text{Ф}\)
\(c=3\cdot 10^8\ \text{м/с}\)

Знайти:
\(\mathbf{\lambda}-?\)

Якщо вважати, що швидкість електромагнітної хвилі в повітрі дорівнює швидкості світла у вакуумі, то довжина радіохвилі, випромінюваної антеною, пов’язана з періодом коливань цієї антени і її контуру співвідношенням \(\mathbf{\lambda}=cT\) (1).

Період коливання коливального контуру обчислюють за формулою Томсона \(T=2\mathbf{\pi}\sqrt{LC}\) (2), де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.

Тож для обчислення періоду потрібно визначити індуктивність котушки в коливальному контурі.

Індуктивність \(L\) – фізична величина, якою характеризують провідник. Вона чисельно дорівнює ЕРС самоіндукції, що виникає в провіднику за зміни сили струму на 1 ампер за 1 секунду.

Тож індуктивність обчислюють за формулою $$ L=\frac{\mathbf{\varepsilon}_{\text{с.і.}}\triangle t}{\triangle I}=\frac{0,0002\cdot 0,6\ \text{с}}{1,2\ \text{А}}=0,0001\ \text{Гн}. $$ Тоді частота коливань антени й отриманої в результаті радіохвилі з виразу (2) дорівнює:

Відповідь: 60.

ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на виявлення зв’язку між періодом коливання і параметрами коливальної системи.

Дано:
\(l_1=2l_2\)
\(T_1=T_2\)

Знайти:
\(\frac{m_2}{m_1}-?\)

Період коливань пружинного маятника визначають за формулою \(T=2\mathbf{\pi}\sqrt{\frac mk}\) (1).

За умовою \(T_1=T_2,\) тож \(2\mathbf{\pi}\sqrt{\frac{m_1}{k_1}}=2\mathbf{\pi}\sqrt{\frac{m_2}{k_2}}\) (2). Тоді \(\frac{m_2}{m_1} =\frac{k_2}{k_1}\) (3).

Нехай ціла пружина мала коефіцієнт жорсткості \(k\). Тоді можна уявити цю початкову пружину як послідовне з’єднання пружин 1 і 2, на які її розрізали за умовою задачі. А коефіцієнти жорсткості \(k_1\) і \(k_2\) цих пружин пов’язані з коефіцієнтом жорсткості першої пружини співвідношенням \(\frac 1k= \frac{1}{k_1}+\frac{1}{k_2}\) (4).

Закон Гука описують формулами \(F_{\text{пруж}}=k|\triangle l|\) (5) і \(\mathbf{\sigma}=E\mathbf{\varepsilon}\) (6), де \(E\) – модуль Юнга матеріалу, \(\mathbf{\sigma}\) – механічна напруга, яку визначають зі співвідношення (7),
а \(\mathbf{\varepsilon}\) – відносне видовження (вираз 8):

Тоді, підставивши (7) і (8) у (6) і прирівнявши вирази для сили пружності з виразів (6) і (5), можна дістати \(k|\triangle l|=SE\frac{|\triangle l|}{l}.\) Тобто \(k=\frac{SE}{l}.\)

Під час розрізання пружини на дві коротші площа перерізу й модуль Юнга не змінюються, тому: \begin{gather*} \frac{k_2}{k_1}=\frac{m_2}{m_1}=\frac{\frac{SE}{l_2}}{\frac{SE}{l_1}}=\frac{l_1}{l_2}=2. \end{gather*}

Відповідь: 2.

ТЕМА: Оптика. Лінза. Оптична сила лінзи.

Завдання скеровано на оцінювання вміння розв’язувати графічні задачі на зображення ходу світлових променів у системах із лінзами.

Оптична сила лінзи \(D\) пов’язана з фокусною відстанню лінзи \(F:\ D=\frac 1F.\)

Для визначення фокусної відстані лінзи потрібно проаналізувати рисунок.

Якщо вважати, що точка перетину променю з оптичною віссю зліва від лінзи – це об’єкт, а справа від лінзи – його зображення, то за формулою тонкої лінзи відстань від об’єкта до лінзи \((d)\), відстань від лінзи до зображення \((f)\) і фокусна відстань пов’язані співвідношенням \(\frac 1F=\frac 1d+\frac 1f\).

На рисунку \(d\) становить шість поділок \((6\cdot 2\ \text{см} = 12\ \text{см} = 0,12\ \text{м})\), а \(f\) – три поділки \((3\cdot 2\ \text{см} = 6\ \text{см} = 0,06\ \text{м}).\) Тобто

Відповідь: 25.

ТЕМА: Квантова фізика. Атом і атомне ядро. Ядерні реакції.

Завдання скеровано на оцінювання вміння виконувати обчислення за рівняннями ядерних реакцій.

Під час радіоактивних розпадів масове число дорівнює кількості нуклонів у ядрі, а зарядове – кількості протонів.

Схема радіоактивного розпаду така: $$ _p^n \mathrm{\boldsymbol X}=_{p-5}^{n-16}\mathrm{\boldsymbol Y}. $$ Під час альфа-розпаду масове число нукліда зменшується на чотири, а зарядове – на два за схемою: $$ _p^n \mathrm{\boldsymbol X}=_{p-2}^{n-4}\mathrm{\boldsymbol Z}+_2^4\mathrm{He}. $$ Масове число може змінюватись лише під час альфа-розпадів, тож для зменшення масового числа на 16 потрібно чотири \(\mathbf{\alpha}\)-розпади.

Після чотирьох \(\mathbf{\alpha}\)-розпадів утвориться нуклід \(_{p-8}^{n-16}\mathrm{\boldsymbol Z}\).

У цього нукліда масове число відповідає тому, що вказано в завданні, а зарядове – на три менше ніж в умові.

Для збільшення зарядового числа має пройти три \(\mathbf{\beta}\)-розпади. Схема \(\mathbf{\beta}\)-розпаду: \(_p^n\mathrm{\boldsymbol X}=_{p+1}^{\ \ \ \ \ n}\mathrm{\boldsymbol X}+_{-1}^{\ \ \ 0} e.\)

Відповідь: 3.