ЗНО онлайн 2020 року з фізики – додаткова сесія

2

ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.

Завдання скеровано на оцінювання розуміння процесу руху кинутого горизонтально тіла, на яке діє сила тяжіння.

Тіло, кинуте під кутом до горизонту, рухається під дією сили тяжіння. Сила тяжіння не змінюється протягом усього руху, й не залежить від того, у якій точці траєкторії перебуває тіло. Не залежить ця сила й від напрямку руху тіла. Тож і прискорення, якого сила тяжіння надає тілу, залишається сталим.

Це прискорення – прискорення вільного падіння \(g = 9,8\ \text{м/с}^2\). Воно збігається за напрямком із силою тяжіння (у напрямку до поверхні землі). Швидкість тіла напрямлена по дотичній до траєкторії в кожній точці, тож її напрямок не збігається з напрямком прискорення (рис. 1).

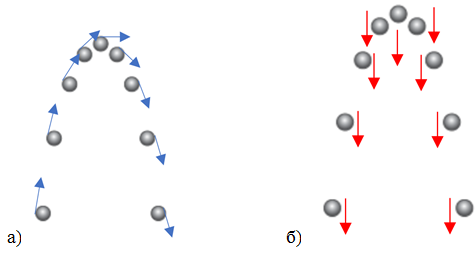
Рис. 1. Схематичне зображення напрямку в різні моменти часу
векторів: а) швидкості \(\overrightarrow{v}\); б) прискорення \(\overrightarrow{g}\)

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівноприскореному русі.

Завдання скеровано на оцінювання вміння аналізувати графіки руху тіл і визначати за ними параметри руху.

У графіку, наведеному в завданні, виокремлено п’ять частин, на кожній із яких відображено різні режими руху тіла. Швидкість руху тіла, відкладену на осі \(y\), визначають за формулою \(v_x=v_0+a_x t\) (1), де \(v_0\) – значення початкової швидкості, \(a_x\) – прискорення, \(t\) – час руху.

Вираз (1) – це рівняння прямої з кутовим коефіцієнтом \(a_x\). Тоді проміжку часу, коли тіло рухається рівноприскорено зі збільшенням модуля швидкості, на графіку відповідає вгорубіжна пряма \((a_x\gt 0)\).

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.

На кульку, що піднімається вгору в повітрі, діють три сили: сила Архімеда, що виштовхує її з товщі повітря вгору, сила тяжіння, яка притягує кульку до землі, і сила опору повітря, що заважає руху кульки (рис. 1). Оскільки сила Архімеда більша за значенням від сили тяжіння, кулька рухатиметься вгору, а сила опору повітря буде напрямлена вниз.

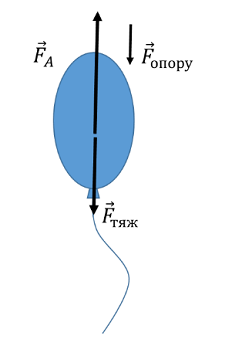
Рис. 1. Сили, що діють на кульку

Рівнодійна \(\overrightarrow{F}\) – це сила, яка здійснює на тіло таку саму дію, як декілька сил, що діють одночасно. Тоді: $$ \overrightarrow{F}=\overrightarrow{F}_A+\overrightarrow{F}_{\text{опору}}+\overrightarrow{F}_{\text{тяж}}\ (1). $$ Для визначення рівнодійної потрібно спроєктувати всі сили, що діють на кульку, на одну вісь – вісь \(Oy\): \begin{gather*} F= F_A-F_{\text{опору}}-F_{\text{тяж}}=\\[7pt] =4Н-1Н-2Н=1Н (2). \end{gather*}

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Момент сил.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення моменту сил.

Момент сили \(M\) – це фізична величина, що дорівнює добутку модуля сили \(F\), яка діє на тіло, на плече \(d\) цієї сили: $$ M = Fd\ \ (1) $$ Плече \(d\) сили \(F\) – це найменша відстань від осі обертання тіла до лінії, уздовж якої діє сила (рис. 1).

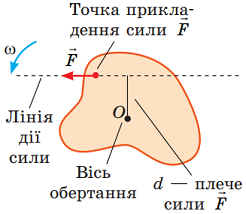
Рис. 1. Схема визначення плеча сили

Проаналізувавши рисунок 2 (його наведено в завданні), потрібно визначити плечі сил, схематично зображених на ньому.

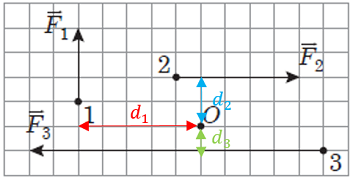
Рис. 2. Визначення плечей сил, про які йдеться в завданні

У завданні не зазначено розмір клітинок, тож можна вважати довжину сторони клітинки умовною одиницею довжини (у. о. д.).

Згідно з виразом (1): \begin{gather*} M_1=F_1 d_1=3Н\cdot\ 5\ \text{у. о. д.}=15Н \cdot\ \text{у.о.д.;}\\[7pt] M_2=F_2 d_2=5Н\cdot\ 2\ \text{у. о. д.}=10Н\cdot\ \text{у.о.д.;}\\[7pt] M_3=F_3 d_3=12Н\cdot\ 1\ \text{у. о. д.}=12Н\cdot\ \text{у.о.д.} \end{gather*} Отже: $$ M_1\gt M_3\gt M_2. $$

Відповідь: A.

ТЕМА: Гідростатичний тиск.

Завдання скеровано на оцінювання розуміння поняття гідростатичного тиску й уміння застосовувати його під час розв’язування розрахункових задач.

Гідростатичний тиск \(p_{\text{гідростат}}\) – тиск нерухомого стовпчика рідини або газу. Його визначають за формулою \(p_{\text{гідростат}}=\mathbf{\rho}gh\), де \(\mathbf{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Якщо вважати, що тиск у повітряних кишенях запаяних трубок однаковий, то тиск у точці B дорівнює тиску в точці Вʹ, а тиск у точці С дорівнює тиску в точці Сʹ. Тиск однорідної рідини на однаковій висоті однаковий, тому можна визначити рівень у воді за межами трубок, який відповідає точкам В і С (рис. 1).

Тиск в точці А дорівнює атмосферному \((p_{\text{атм}})\), а в точці Вʹ і в точці Сʹ тиск дорівнює сумі атмосферного й гідростатичного тиску: $$p = p_{\text{атм}}+p_{\text{гідростат}}.$$ Оскільки \(h_B\gt h_C,\) то \(p_{\text{гідростат B}}\gt p_{\text{гідростат C}},\) то \(p_B\gt p_C.\) Оскільки \(p_С\gt p_А,\) то \(p_B\gt p_C\gt p_А.\)

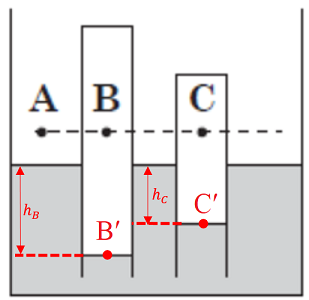
Рис. 1. Визначення гідростатичного тиску

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Процес 1–2 є ізохорним (тиск \(p\) й температура \(T\) зростають за сталого
об’єму \(V\)).

Процес 2–3 – ізобарним (температура \(T\) зростає, об’єм \(V\) за сталого тиску \(p\)).

Відповідно в координатах \(pV\) процес 1–2 відображено перпендикулярною до осі \(V\) прямою, напрямленою вгору, бо тиск зростає, а процес 2–3 – перпендикулярною до осі \(p\) прямою, напрямленою вправо, бо об’єм збільшується.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рівняння теплового балансу й стану теплової рівноваги.

У калорифері вода й лід обмінюються теплотою, щоби досягти стану теплової рівноваги. Передусім потрібно оцінити, яка кількість теплоти потрібна для охолодження всієї води до температури замерзання \((0\ ^{\circ}\text{С})\):

Затим треба розрахувати кількість теплоти, необхідної дня нагрівання льоду до температури плавлення \((0\ ^{\circ}\text{С})\):

Оскільки \(Q_{\text{нагрівання}}\lt Q_{\text{охолодження}}\), то навіть після того весь лід буде нагріто до температури \(0\ ^{\circ}\text{С}\), вода все ще не охолодиться до цієї температури й віддасть льоду решту теплоти, що витратиться на процес його танення:

Наступний крок розв’язання полягає в обчисленні кількості теплоти, потрібної для того, щоби лід повністю розтанув:

\(Q_{\text{танення}}\gt Q_{\text{охолодження}}-Q_{\text{нагрівання}},\) тому лише частина льоду розтане, після чого система прийде до стану теплової рівноваги за температури \(0\ ^{\circ}\text{С}.\)

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Перший закон термодинаміки.

Завдання скеровано на оцінювання розуміння першого закону термодинаміки.

За першим законом термодинаміки \(Q = \triangle U + A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

Відповідно зміна внутрішньої енергії \(\triangle U = Q\ – A.\)

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.

Завдання скеровано на оцінювання розуміння поняття напруженості електричного поля і вміння порівнювати її значення в різних точках електричного поля.

На рисунку зображено позитивний заряд, який створює навколо себе електричне поле. Для порівняння напруженості електричного поля і потенціалу в точки А і В потрібно помістити пробний заряд \(Q\).

Напруженість електричного поля \((\overrightarrow{E})\) у певній точці – векторна фізична величина, яка характеризує електричне поле й дорівнює відношенню сили \(\overrightarrow{F}\), із якою електричне поле діє на пробний заряд, поміщений у цю точку поля, до величини цього заряду: $$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q}. $$

На пробний заряд з боку поля діє сила Кулона, модуль якої \(F=k\frac{|Q||q|}{r^2},\) де \(r\) – відстань між зарядами, а \(k=9\cdot 10^9\ \text{Нм}^2/\text{Кл}^2\).

Відстань між лініями сітки в цій задачі не зазначено, тому можна вважати, що її вимірюють в умовних одиницях довжини (у. о. д.).

Тоді \(r_A=2\ \text{у. о. д},\) а \(r_В=4\ \text{у. о. д},\) тобто \(r_В=2r_А.\) Напруженість поля в точках А і В відповідно становить: \begin{gather*} E_A=\frac Fq=\frac{k|Q||q|}{r^2_A q}=\frac{k|Q|}{r^2_A};\\[7pt] E_B=\frac Fq=\frac{k|Q||q|}{r^2_B q}=\frac{k|Q|}{r^2_B}=\frac{k|Q|}{4r^2_A}. \end{gather*} Відповідно \(E_A=4E_В.\)

Відповідь: A.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Ома для ділянки електричного кола.

За законом Ома \(I= \frac UR,\) де \(I\) – сила струму, яку вимірюють в А (амперах), \(U\) – напруга, що вимірюють у В (вольтах), \(R\) – опір, який вимірюють в Ом (омах).

За умовою на цоколі лампи зазначено величини в вольтах й амперах, тобто йдеться про робочу напругу й силу струму лампи. Величини робочої напруги й сили струму ламп, а також їхнього опору в робочому стані, обчисленого за формулою \(R= \frac UI\) наведено в таблиці:

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.

Завдання скеровано на оцінювання розуміння поняття електричного заряду, вільних носіїв заряду і їхнього передавання під час електричної взаємодії.

Позитивно заряджені частинки всередині ядра атома – це протони, а негативно заряджені частинки, що рухаються навколо ядра, – електрони. Відокремити протон від ядра дуже складно, тому під час таких електричних явищ, як, наприклад, зарядження шерсті внаслідок тертя, зміни кількості протонів у ядрах не відбувається.

Атоми зберігають свою нейтральність за рахунок однакової кількості протонів й електронів. Відповідно, щоби зарядитися позитивно, атоми речовини повинні віддати частину своїх електронів, а щоби зарядитись негативно – захопити додаткові електрони.

Оскільки за умовою завдання шерсть набуває позитивного заряду, то саме вона віддає паличці свої електрони.

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.

Завдання скеровано на оцінювання вміння розраховувати модуль сили Ампера для провідників зі струмом під дією магнітного поля.

Сила Ампера – це сила, що діє на провідник зі струмом в магнітному полі. Її напрямок визначають за правилом лівої руки, а модуль – за формулою $$ F_A=BIl$1\mathbf{\alpha}, $$ де \(B\) – магнітна індукція, \(I\) – сила струму в провіднику, \(l\) – довжина провідника,
\(\mathbf{\alpha}\) – кут між напрямком струму й вектором магнітної індукції.

Оскільки сила струмі \(I\) й магнітна індукція \(B\) не дорівнюють нулю в жодному випадку з-поміж зображених на рисунку, необхідно визначити, коли \($1\mathbf{\alpha}=0.\)
У цьому разі напрямок сили струму й напрямок ліній магнітної індукції є або паралельними \((\mathbf{\alpha} = 0^\circ)\), або антипаралельними \((\mathbf{\alpha} = 180^\circ).\)

Лінії магнітної індукції проводять від північного полюса до південного, тож у випадках A, B і Г \(\mathbf{\alpha} = 90^\circ,\) а у випадку Б \(\mathbf{\alpha} = 180^\circ.\)

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Електростатичний потенціал.

Завдання скеровано на оцінювання розуміння понять електростатичного потенціалу, різниці потенціалів і роботи електричного поля з перенесення заряду й уміння розв’язувати розрахункові задачі, пов’язані із цими поняттями.

Потенціал \(\mathbf{\varphi}\) електростатичного поля в даній точці – це скалярна фізична величина, яка характеризує енергетичні властивості поля.

Для точкового заряду потенціал можна розрахувати за формулою \(\mathbf{\varphi}=k\frac Qr,\)
де \(r\) – відстань між зарядом і пробним зарядом, поміщеним у його поле, \(k = 9\cdot 10^9\ \text{Н}\cdot\text{м}^2/\text{Кл}^2,\) а \(Q\) – величина заряду, що створює поле.

Різниця потенціалів – скалярна фізична величина, яка дорівнює відношенню роботи сил електростатичного поля з переміщення заряду з початкової точки в кінцеву до значення цього заряду: \(\triangle\mathbf{\varphi}=\mathbf{\varphi}_2-\mathbf{\varphi}_1=\frac Aq.\)

Тож робота, виконувана полем під час перенесення заряду залежить від різниці потенціалів між початковою і кінцевою точкою: чим менша ця різниця, тим менша (за модулем) виконувана робота.

З огляду на те, що точки О і Г лежать на одній еквіпотенціальній поверхні, то \(\mathbf{\varphi}_{\text{O}}=\mathbf{\varphi}_{\text{Г}},\) а \(\triangle\mathbf{\varphi}=\mathbf{\varphi}_{\text{Г}}-\mathbf{\varphi}_{\text{O}}=0.\)

Інші точки лежать на інших еквіпотенціальних поверхнях, тому найменшу (за модулем) роботу \(A\) буде виконано під час переміщення в Г \((A = 0).\)

Відповідь: Г.

ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з виявлення зв’язку між періодом коливання і параметрами коливальної системи.

Період коливання \(T\) пружинного маятника обчислюють за формулою $$ T=2\mathbf{\pi}\sqrt{\frac mk}, $$ де \(m\) – маса тягарця, а \(k\) – коефіцієнт жорсткості пружини.

Якщо вдвоє скласти гумову нитку, яка виконує функцію пружини, то утвориться маятник, що коливається на двох удвічі менших пружинах, з’єднаних паралельно. Тоді до складання велику пружину (гумову нитку) можемо вважати двома половинками, що з’єднані послідовно.

Якщо є дві пружини із жорсткістю \(k_1\) і \(k_2\) відповідно, то можна визначити жорсткість пружин, які відповідають паралельному й послідовному їхньому з’єднанню.

Для паралельного з’єднання пружин їхня жорсткість \(k' = k_1 + k_2.\)

Для послідовного з’єднання жорсткість $$ k=\frac{k_1 k_2}{k_1+k_2}. $$

Половинки пружини мають однакову жорсткість і \(k_1 = k_2 = k'',\) тому жорсткість $$ k= \frac{(k'')^2}{2k''}=\frac{k''}{2}. $$

Оскільки \(k'' = 2k,\) жорсткість кожної половинки вдвічі більша за жорсткість початкової пружини (гумової нитки).

Якщо з’єднати ці дві половинки паралельно, то отримана пружина матиме жорсткість \(k'= k''+ k''= 2k''.\)

Тоді період такої пружини дорівнюватиме

Порівняння його з періодом коливання \(T\) пружинного маятника \(T=2\mathbf{\pi}\sqrt{\frac mk}\) дає змогу дійти висновку, що \(T'=1/2T.\)

Відповідь: Б.

ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на оцінювання вміння аналізувати рівняння і графік гармонічних коливань, визначати основні фізичні величини, пов’язані з ними.

На рисунку зображено графік гармонічних коливань величини електрорушійної сили (ЕРС) залежно від часу.

Загальний вигляд рівняння гармонічних коливань такий: \begin{gather*} x=A$1(\mathbf{\omega}t+\mathbf{\varphi}_0)\\[7pt] \text{або}\ x=A$1(\mathbf{\omega}t+\mathbf{\varphi}_0), \end{gather*} де \(x\) – координата, \(\mathbf{\omega}\) – циклічна частота коливань, \(\mathbf{\varphi}_0\) – початкова фаза коливань, \(t\) – час.

Обидва варіанти цього рівняння можуть описувати будь-які гармонічні коливання, і єдине, що зміниться внаслідок переходу від рівняння із функцією синус до рівняння з функцією косинус, – це початкова фаза коливань.

Початкова фаза коливань – фаза коливань у момент початку відліку часу.

На рисунку до завдання в точці \(t = 0\) – відхилення від положення рівновагидорівнює 0. Таку криву в загальному випадку описують рівняннями \begin{gather*} x=A$1(\mathbf{\omega}t+\mathbf{\varphi}_0)\\[7pt] \text{або}\ x=A$1(\mathbf{\omega}t+\frac{\mathbf{\pi}}{2}), \end{gather*} де \(\frac{\mathbf{\pi}}{2}\) – початкова фаза.

Амплітуда коливань – це максимальне відхилення від положення рівноваги. Його можна визначити за рисунком – це відстань від осі \(x\) (рівня рівноваги) до максимуму або мінімуму синусоїди. \(A = 40\ \text{B}\).

Циклічну частоту \(\mathbf{\omega}\) можна визначити з рівності \(\mathbf{\omega}=\frac{\mathbf{2\pi}}{T}\), де \(T\) – період коливань.

Період коливань – це час, за який коливання повністю повторюється.

Можна визначити період коливань за рисунком. Це відстань між двома максимумами синусоїди: $$ T = 0,5\ \text{c} - 0,1\ \text{c}=0,4\ \text{c}. $$ Тоді \(\mathbf{\omega}=\frac{2\mathbf{\pi}}{0,4}=5\mathbf{\pi}\).

Далі потрібно підставити всі визначені величини в рівняння гармонічних коливань: $$ x=40$1(5\mathbf{\pi}t)\ \text{або}\ x=40$1(5\mathbf{\pi}t+\frac{\mathbf{\pi}}{2}). $$

Відповідь: Б.

ТЕМА: Механічні коливання і хвилі. Частота й період коливань.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження параметрів коливань частинок хвилі.

Паперовий кораблик на гребені хвилі коливається так само, як і частинки води у хвилі.

Під час коливань за один період тіло повертається в початкове положення. Якщо вважати, що в початковий момент часу кораблик був у точці максимального відхилення рівноваги, то за чверть періоду він опиниться на рівні спокійної води, а за наступну чверть – у точці максимального відхилення від положення рівноваги з іншого боку від рівня рівноваги, тобто в найнижчому положенні.

Якщо частота коливань $$ v= 2\ \text{Гц} = 2\frac{1}{\text{c}}, $$ то період коливань $$ T=\frac 1v=\frac 12\text{c}=0,5\ \text{c}. $$

Тоді, оскільки кораблик опиниться в найнижчій точці за половину періоду, можна обчислити цей час: $$ 2)\ t=\frac T2=0,25\ \text{c}. $$

Відповідь: A.

ТЕМА: Оптика. Закони відбивання і заломлення світла. Лінза. Дифракційна ґратка.

Завдання скеровано на оцінювання розуміння принципів роботи оптичних елементів.

До оптичного елемента на рисунку, наведеному в умові завдання, пучок променів розширюється, а після – перетворюється на пучок паралельних променів.

Пучок не може стати паралельним після проходження через плоске дзеркало чи дифракційну ґратку за жодних обставин.

Щодо лінз: якщо пучок виходить із фокусу лінзи, після неї промені будуть паралельними, але ця умова набирає різних форм для розсіювальних і збиральних лінз. Для розсіювальної лінзи продовження напрямку променів до лінзи мають збиратись у фокусі за лінзою (рис. 1), тобто пучок до лінзи повинен звужуватись, а для збиральної лінзи пучок має виходити із фокусу перед лінзою, тобто пучок розширюватиметься (рис. 2).

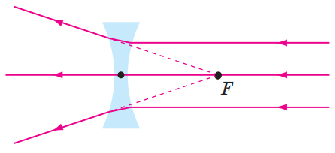
Рис. 1. Хід променів у розсіювальній лінзі

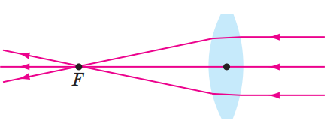
Рис. 2. Хід променів у збиральній лінзі

Відповідь: Б.

ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.

Завдання скеровано на оцінювання розуміння ядерної взаємодії між частинками.

\(\mathbf{\alpha}\)-Частинка – позитивно заряджена важка частинка (ядро атома Гелію). Зазвичай α-частинки мають дуже велику кінетичну енергію і саме завдяки цьому можуть наблизитися до ядра й увійти в радіус дії ядерних сил.

За малої кінетичної енергії в силу вступлять електричні сили, і заряджена позитивно \(\mathbf{\alpha}\)-частинка відштовхуватиметься від ядра. З тієї самої причини ядро не захопить позитивно заряджений протон із малою кінетичною енергією. Оскільки нейтрон є електронейтральною частинкою, ядро захоплюватиме його без перешкод від кулонівської взаємодії. Експериментально доведено, що повільні нейтрони ядро захоплює ліпше за швидкі.

Ядро зрідка захоплює електрони. Коли це трапляється, то ядро захоплює ті електрони свого атома, що перебувають найближче до ядра. Це приводить до зменшення кількості протонів у ядрі на один. Зокрема, електричний струм у провідниках – це потік вільних електронів. І якби ядра захоплювали електрони під час проходження струму, будь-яке явище електрики супроводжували б активні ядерні реакції, що зазвичай не відбувається.

Відповідь: Г.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання розуміння законів фотоефекту.

Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.

За першим законом фотоефекту кількість фотоелектронів, випромінюваних катодом за одиницю часу, прямо пропорційна інтенсивності світла.

За умовою завдання потужність джерела зменшилася вдвічі, а отже й інтенсивність випромінювання змінилася так само. Тоді за першим законом фотоефекту кількість випромінених електронів також зменшилася вдвічі.

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на оцінювання розуміння природи кінетичної і потенціальної енергії.

Кінетична енергія \(E_k\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху.

Потенціальна енергія \(E_p\) – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою.

Для тіл, що перебувають у полі сили тяжіння (як тіла із завдання), потенціальну енергію визначають за формулою $$ E_p = mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.

Кінетичну енергію тіла обчислюють за формулою $$ E_k=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, а \(v\) – швидкість його руху.

Щодо ситуацій, описаних у завданні:

A Кулька, що вільно падає вниз, утрачає висоту, а отже її потенціальна енергія зменшується. До того ж тіло, що вільно падає, рухається лише під дією сили тяжіння з постійним прискоренням (прискоренням вільного падіння, що спрямоване до поверхні землі), отже швидкість тіла, яка спрямована до поверхні землі, збільшується, а разом із нею збільшується і кінетична енергія.

Б М’ячик, що рухається вгору, набирає висоту, а його потенціальна енергія збільшується. Оскільки напрямок швидкості м’ячика протилежний напрямку прискорення вільного падіння, то швидкість, а разом із нею і кінетична енергія зменшуються.

В Парашутист опускається на землю, його висота над поверхнею землі зменшується, що приводить до зменшення потенціальної енергії. Оскільки парашутист рухається рівномірно, то його швидкість не змінюється під час спуску, тож його кінетична енергія також не змінюється.

Г Літак, що летить на певній висоті з постійною швидкістю не змінює ні висоти відносно поверхні землі, ні (відповідно до умови) своєї швидкості, а отже його як кінетична, так і потенціальна енергія залишаються сталими.

Відповідь: 1А, 2В, 3Г, 4Д.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її зміни. Способи теплопередачі.

Завдання скеровано на оцінювання розуміння різних механізмів теплопередачі.

Теплопередача (теплообмін) – процес зміни внутрішньої енергії тіла або частин тіла без виконання роботи.

Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу.

Теплопровідність – це вид теплопередачі, зумовлений хаотичним рухом частинок речовини й не супроводжуваний перенесенням цієї речовини.

Випромінювання – це вид теплопередачі, за якого енергія передається за допомогою електромагнітних хвиль.

Конденсація – це процес переходу речовини з газуватого стану в рідкий

Робота \(A\) – це фізична величина, яка характеризує зміну механічного стану тіла.

Щодо ситуацій, описаних у завданні:

A Нагрівання в мікрохвильовій печі відбувається за рахунок проникнення мікрохвильового випромінювання в об’єм їжі.

Б Стіни будинку взимку нагріваються за допомогою внутрішнього опалення. Через це утворюється різниця температур між стінами й повітрям зовні. Тож аби досягти теплової рівноваги стіни віддаватимуть теплоту навколишньому середовищу без переносу речовини, із якої вони збудовані, тобто братимуть участь у теплообміні.

В Теплота передається всьому об’єму води завдяки тому, що гаряча вода має меншу густину ніж холодна, тому вона підніматиметься й обмінюватиметься теплом із холоднішою водою навколо. Тобто в окропі утворюються потоки рідини, які переносять тепло, а тому відбувається конвекція.

Г Під час тертя долонь одна об одну механічна енергія руху частково переходить у теплову за рахунок роботи сили тертя.

Відповідь: 1Б, 2Д, 3В, 4А.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах.

Завдання скеровано на оцінювання розуміння різних видів газових розрядів й умов їхнього застосування в техніці.

Дуговий газовий розряд виникає за високої температури (понад 4000 °С) і майже за будь-якого тиску. Його характерною ознакою є яскраве дугоподібне полум’я. За такої високої температури з поверхні катода безперервно «випаровуються» електрони, а в стовпі розпеченого газу відбувається термічна йонізація. Це забезпечує ідеальні умови для впливу на металеві поверхні без прямого контакту приладу з ними.

Іскровий газовий розряд виникає за атмосферного тиску й великої напруги між електродами. Тривалість іскрового газового розряду дуже мала, тому його часто використовують під час підпалювання робочої суміші в циліндрі двигуна внутрішнього згоряння. Цикл усередині циліндра загалом займає мало часу й потребує швидкого нагрівання для роботи.

Тліючий (жеврійний) газовий розряд виникає за невеликої напруги між електродами й низького тиску. Цей тип розряду приводить до жеврійного світіння в трубках із низьким тиском газу навіть під дією слабкого електричного поля, що робить його найзручнішим для використання в освітленні.

Коронний газовий розряд виникає за тиску, близького до атмосферного в сильному \((E\gt 500\ \text{кВ/м}),\) різко неоднорідному електричному полі. Велике поле змушує йони рухатись із великою швидкістю і, як наслідок, великою кінетичною енергією, що викликає ударну йонізацію. Численні йони газу під час проходження між електронами заряджають дрібні частинки пилу, що також рухаються в полі й осідають на одному з електродів, звідки їх легко прибрати.

Відповідь: 1В, 2Д, 3А, 4Г.

ТЕМА: Оптика. Лінза. Плоске дзеркало.

Завдання скеровано на оцінювання розуміння принципів роботи оптичних елементів під час проходження крізь них паралельних променів.

Оптична сила лінзи \(D\) – це фізична величина, яка характеризує заломні властивості лінзи й обернена до її фокусної відстані. Для збиральних лінз вона додатна, а для розсіювальних – від’ємна. Тоді тонка лінза, описана в пункті 1 – збиральна, а в пункті 2 – розсіювальна. Для цих оптичних елементів схема ходу променів така:

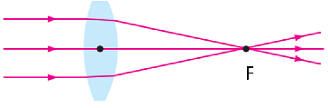
Рис. 1. Хід променів після проходження збиральної лінзи

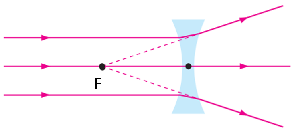
Рис. 2. Хід променів після проходження розсіювальної лінзи

Плоскопаралельна пластинка – це оптичний елемент, у якого дві заломлювальні поверхні паралельні одна одній. Тобто можна уявити шар скла для опису проходження променів.

За законом заломлення променів \(n_1$1⁡}(\mathbf{\alpha})=n_2$1⁡}(\mathbf{\beta}),\) де \(n_1\) і \(n_2\) – це відповідні абсолютні показники заломлення речовин, між якими відбувається перехід,
\(\mathbf{\alpha}\) – кут падіння променів, \(\mathbf{\beta}\) – кут заломлення променів.

Якщо встановити плоскопаралельну пластинку так само, як схематично зображено на рисунках 1 і 2, то кут \(\mathbf{\alpha}=0,\ n_2$1⁡}(\mathbf{\beta})=0.\) Тобто кут \(\mathbf{\beta}=0.\)

Оскільки кут заломлення дорівнює нулю, то напрямок променів не змінився. Цей розрахунок застосований для будь-якого променя з паралельного пучка. Оскільки жоден із них не змінить напрямку, то вони залишаться паралельними.

Унаслідок відбивання від плоского дзеркала напрямок променя зміниться, але за законами відбивання кут падіння дорівнюватиме куту відбивання. Якщо пучок складався з паралельних променів, то вони всі падали на поверхню дзеркала під однаковим кутом, а отже й відбиватимуться також під однаковим кутом, що не порушить їхньої взаємної паралельності, як показано на рисунку 3.

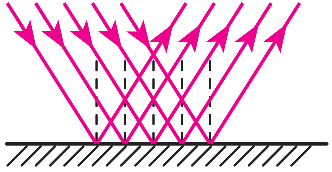
Рис. 3. Відбивання паралельних променів від плоского дзеркала

Відповідь: 1Б, 2А, 3В, 4Г.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і застосовувати перший закон термодинаміки для них.

1. Знайти:
\(p_2\ (\text{кПа})-?\)

За графіком процесу 1–2 (поділками на осі y) можна визначити тиск у закритій посудині у стані 2. Оскільки великі поділки підписано через одну, і перша підписана поділка – це \(2\cdot 10^5\ \text{Па},\) легко дійти висновку, що ціна великої поділки – \(1\cdot 10^5\ \text{Па}.\) Тоді ціна маленької поділки, яка ділить велику навпіл, дорівнює \(0,5\cdot 10^5\ \text{Па}.\)

З огляду на це у стані 2 тиск \(p_2=0,5\cdot 10^5\ \text{Па}=50\ \text{кПа}.\)

2. Знайти:
\(A\ (\text{кДж}) - ?\)

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

У координатах \(pV\) параболою зображено ізотермічний (за сталої температури) процес. У такому разі зміна внутрішньої енергії дорівнює нулю, тоді
\(Q=A=3\cdot 10^5\ \text{Дж}=300\ \text{кДж}.\)

Відповідь: 1. 50. 2. 300.

ТЕМА: Механіка. Основи динаміки. Умови рівноваги.

Завдання скеровано на оцінювання вміння використовувати умови рівноваги для розв’язування розрахункових задач.

Дано:
\(m_{\text{довге}}=400\ \text{г}\)
\(m_{\text{коротке}}=900\ \text{г}\)

1. Знайти:
\(m (\text{кг})-?\)

Важіль за умовою перебуває в рівновазі в обох випадках, отже сума моментів сил, що діють на нього, дорівнює нулю.

Момент сили \(M\) – це фізична величина, що дорівнює добутку модуля сили \(F\), яка діє на тіло, на плече \(d\) цієї сили: $$ M=Fd\ (1) $$

Щодо плеча сил для короткого й довгого плеча важеля: їхні довжини залишатимуться незмінними за заміни вантажів.

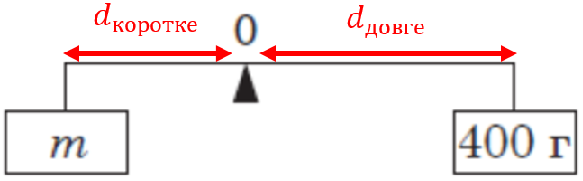
Рис. 1. Визначення плеча сили для важеля

Тоді, за умовою рівноваги важеля, \(M_{\text{довге}}=M_{\text{коротке}}\ (2).\)

І для всіх вантажів, про які йдеться в задачі, \(F=P=mg\ (3).\)

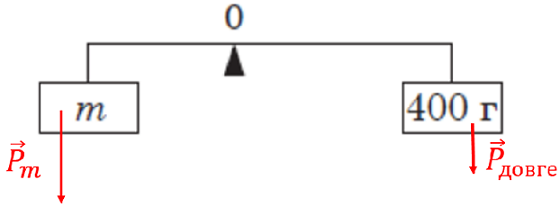
Рис. 2. Схематичне зображення дії сил на вантажі

Аналогічно тому, що зображено на рисунку 2, для ситуації, коли невідомий вантаж прикріплено до короткого плеча, можна розставити сили для ситуації, коли він прикріплений до довгого плеча.

Тож, скориставшись виразами (1), (2) і (3), можна записати систему рівнянь (4):

Потім потрібно поділити верхнє рівняння із системи (4) на нижнє:

Тоді з (5) можна виразити \(m\) – невідому масу тягарця:

2. Знайти:
\(\frac{d_{\text{довге}}}{d_{\text{коротке}}} - ?\)

З виразу (4) випливає, що \(d_{\text{довге}}m_{\text{довге}}=d_{\text{коротке}}m\ (7).\)

Тоді відношення \(\frac{d_{\text{довге}}}{d_{\text{коротке}}}\) можна виразити так: $$ \frac{d_{\text{довге}}}{d_{\text{коротке}}}=\frac{m}{m_{\text{довге}}}=\frac{600\ \text{г}}{400\ \text{г}}=1,5\ (8). $$

Відповідь: 1. 600. 2. 1,5.

ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.

Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото, і розв’язувати розрахункові задачі з використанням законів Ома.

1. Знайти:
\(U_{1R_1}(B)-?\)

Схема електричного ланцюга, зображеного на фото 1 в умові завдання, така:

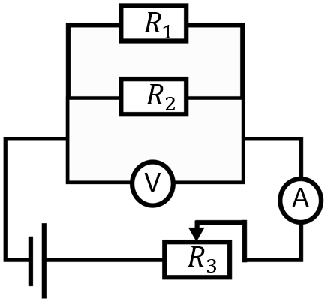
Рис. 1. Схема електричного ланцюга до розімкнення ключа

Реостат послідовно підключено до двох резисторів, підімкнутих паралельно.

Правила для послідовного підключення провідників, схематично зображеного на рисунку 2, описано формулами \(U=U_1+U_2,\ R=R_1+R_2,\ I=I_1=I_2,\)
де \(U\) – напруга, \(R\) – опір, \(I\) – сила струму. Тому сила струму, яку вимірює амперметр – це сила струму на реостаті й на системі паралельно підключених провідників. За показаннями на фото вона дорівнює \(1,5\ \text{A}.\)

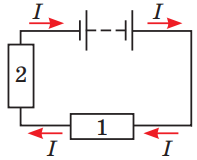
Рис. 2. Послідовне з’єднання провідників 1 і 2

Для паралельно підключених провідників (рис. 3) діють правила, описані формулами: \begin{gather*} U=U_1=U_2,\\ \frac 1R=\frac{1}{R_1}+\frac{1}{R_2},\\ I=I_1+I2. \end{gather*}

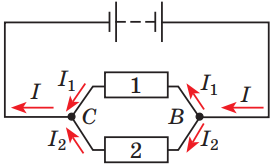
Рис. 3. Паралельне з’єднання провідників 1 і 2

Напруга, яку вимірює вольтметр, – це напруга в системі паралельно підключених провідників. А напруга \(U_1\) на кожному з них дорівнює виміряній напрузі й становить \(2\ \text{B}.\)

2. Знайти::
\(R_1 - ?\)

Після розімкнення ключа електричне коло змінилося – струм по гілці \(R_1\) більше не тече. Тому схема, зображена на рисунку 1, зазнає видозміни (рис. 4).

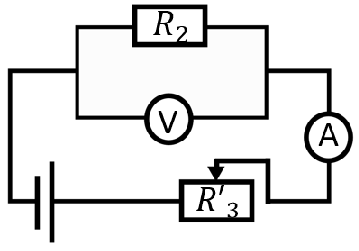
Рис. 4. Схема після розімкнення ключа

Тепер амперметр вимірює силу струму на реостаті з новим значенням опору й провіднику \(R_2,\) і вона за умовами задачі залишається сталою, а вольтметр вимірює напругу \(U_2\) лише на провіднику \(R_2,\) вона дорівнює \(3\ \text{В}.\)

Напруга, сила струму й опір на ділянці електричного кола пов’язані законом Ома, який описано формулою: $$ I=\frac UR. $$

Тоді, знаючи силу струму й напругу на двох провідниках до відключення і провіднику \(R_2\) після відключення, можна скласти систему рівнянь. Якщо сумарний опір провідників у цій системі позначити \(R_{\text{до}},\) то за виразом для опору паралельно під’єднаних провідників можна визначити його: $$ \frac{1}{R_{\text{до}}}=\frac{1}{R_1}+\frac{1}{R_2},\ \ R_{\text{до}}=\frac{R_1R_2}{R_1+R_2}. $$

Після складання системи рівнянь \begin{gather*} \begin{cases} I=\frac{U_1}{R_{\text{до}}}\\ I=\frac{U_2}{R_2} \end{cases} \end{gather*} її перетворюють, підставивши замість \(R_{\text{до}}\) вираз \(\frac{R_1R_2}{R_1+R_2}.\) $$ \begin{cases} I=\frac{U_1(R_1+R_2)}{R_1R_2}\\ I=\frac{U_2}{R_2} \end{cases}. $$

Із рівняння, складеного для кола після розімкнення ключа, можна визначити
опір \(R_2:\) $$ R_2=\frac{U_2}{I}=\frac{3\ \text{B}}{1,5\ \text{A}}=2\ \text{Ом}. $$ Оскільки

Відповідь: 1. 2. 2. 4.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення основних кінематичних величин за рівномірного руху.

Дано:
\(\triangle t=2,25\ \text{c}\)
\(v_{\text{звуку}}=340\ \text{м/с}\)
\(v_{\text{кулі}}=680\ \text{м/с}\)

1. Знайти:
\(\frac{t_{\text{кулі}}}{t_{\text{звуку}}}-?\)

Нехай \(t_{\text{кулі}}\) – це час, який знадобився кулі, щоби пройти шлях \(l\) від спортсмена до мішені, а \(t_{\text{звуку}}\) – це час, який знадобився, аби звук удару кулі об мішень дійшов до спортсмена.

З огляду на те, що відстані, яку подолали куля і звукова хвиля, рівні, а швидкості руху кулі й поширення звуку відомі, можна виразити обидва проміжки часу: $$ t_{\text{кулі}}=\frac{l}{v_{\text{кулі}}},\ \ t_{\text{звуку}}=\frac{l}{v_{\text{звуку}}}. $$

Тоді справедливим буде таке співвідношення: \begin{gather*} \frac{t_{\text{кулі}}}{t_{\text{звуку}}}=\frac{\frac{l}{v_{\text{кулі}}}}{\frac{l}{v_{\text{звуку}}}}=\frac{v_{\text{звуку}}}{v_{\text{кулі}}}=\frac{340\ \text{м/с}}{680\ \text{м/с}}=0,5. \end{gather*}

2. Знайти::
\(l\ \text{(м)} - ?\)

Куля пройшла шлях від спортсмена до мішені, а потім звук від удару кулі об мішень повернувся назад до спортсмена. Тоді час від вистрілу до моменту, коли спортсмен почув звук цього удару, можна записати як суму цих двох проміжків часу: $$ \triangle t=t_{\text{кулі}}+t_{\text{звуку}}. $$

Потім потрібно виконати підстановки й здійснити перетворення: \begin{gather*} \triangle t=0,5t_{\text{звуку}}+t_{\text{звуку}}=1,5t_{\text{звуку}},\\[6pt] t_{\text{звуку}}=\frac{2,25\ \text{c}}{1,5}=1,5\ \text{c}; \end{gather*}

Після цього можна обчислити шукану відстань \(l\): $$ l=t_{\text{звуку}}v_{\text{звуку}}=1,5\ \text{c}\cdot 340\frac{\text{м}}{\text{c}}=510\ \text{м}. $$

Відповідь: 1. 0,5. 2. 510.

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення основних кінематичних величин за рівноприскореного руху.

Дано:
\(h_1=5\ \text{м}\)
\(h_2=10\ \text{м}\)
\(v_{01}=0\ \text{м/с}\)
\(t_1=t_2\)

Знайти:
\(v_{02}-?\)

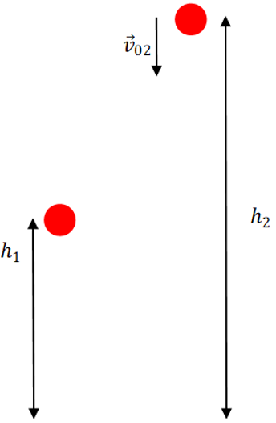
Рис. 1. Схема руху двох тіл

Обидва тіла рухаються лише під дією сили тяжіння, тож їхній рух – рівноприскорений. Оскільки переміщення \(s\), зроблені кожною з кульок, відомі, то залежність переміщення від часу для рівноприскореного руху описано формулою: $$ s=v_0t+\frac{at^2}{2}\ \ (1), $$ де \(v_0\) – початкова швидкість, \(a\) – прискорення, \(t\) – час руху тіла.

Тож можна записати переміщення для тіл, про які йдеться в завданні, узявши до уваги, що переміщення \(s\) першого й другого тіл дорівнюватимуть \(h_1\) і \(h_2\) відповідно, а прискорення \(a\) – прискоренню вільного падіння \((g = 10\ \text{м/с}^2)\) в обох випадках. Тоді можна записати таку систему рівнянь: $$ \begin{cases} h_1=\frac{gt_1^2}{2};\\ h_2=v_{02}t_2+\frac{gt_2^2}{2}. \end{cases} $$

Оскільки приземлитись тіла мають одночасно, то \(t_1=t_2=t:\) $$ \begin{cases} h_1=\frac{>^2}{2};\\ h_2=v_{02}t+\frac{>^2}{2}. \end{cases} $$

Із першого рівняння системи можна виразити час падіння \(t\) і підставити його в друге рівняння цієї самої системи: $$ \begin{cases} t=\sqrt{\frac{2h_1}{g}};\\ h_2=v_{02}\sqrt{\frac{2h_1}{g}}+\frac{g\frac{2h_1}{g}}{2}=v_{02}\sqrt{\frac{2h_1}{g}}+h_1. \end{cases} $$

Тоді з другого рівняння системи можна виразити початкову швидкість другого тіла: $$ v_{02}=\frac{h_2-h_1}{\sqrt{\frac{2h_1}{g}}}=\frac{10\ \text{м}-5\ \text{м}}{\sqrt{\frac{2\cdot 5\ \text{м}}{10\ \text{м/c}^2}}}=5\ \frac{\text{м}}{\text{c}}. $$

Відповідь: 5.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу. Ізопроцеси в газах. Внутрішня енергія і способи її зміни.

Завдання скеровано на оцінювання вміння визначати зміну внутрішньої енергії ідеального газу за зміною його макроскопічних параметрів, використовувати перший закон термодинаміки для ізопроцесів і розв’язувати розрахункові задачі, пов’язані із цими поняттями.

Дано:
\(A=8\ \text{кДж}\)
\(p=\mathrm{const}\)

Знайти:
\(Q\ (\text{кДж})-?\)

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

Зміну внутрішньої енергії одноатомного ідеального газу можна обчислити, використавши вираз $$ \triangle U=\frac 32 nR\triangle T, $$ де \(n\) – кількість речовини ідеального газу, \(R\) – універсальна газова стала,
\(\triangle T\) – зміна температури газу.

Оскільки зміна температури невідома, потрібно використати рівняння стану ідеального газу $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура,
\(n\) – кількість речовини.

Процес у завданні перевів ідеальний газ зі стану 1 \((p_1,T_1,V_1)\) у стан 2 \((p_2,T_2,V_2).\)

За умовою \(p_1=p_2=p.\)

Тоді \(\triangle T=T_2-T_1,\) a $$ \triangle U=\frac 32 nR(T_2-T_1)=\frac 32(nRT_2-nRT_1). $$

За допомогою рівняння стану ідеального газу можна замінити \(nRT_2\) та \(nRT_1\):

Роботу в довільному термодинамічному процесі можна обчислити як площу криволінійної трапеції під графіком залежності \(p(V),\) а для ізобраного процесу її можна розрахувати за формулою \(A=p\triangle V=8\ \text{кДж}.\)

Після підстановки й перетворень можна обчислити шукану кількість теплоти:

Відповідь: 20.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Робота. Потужність. ККД теплового двигуна.

Завдання скеровано на оцінювання розуміння понять потужності й коефіцієнту корисної дії (ККД) теплової машини й уміння розв’язувати розрахункові задачі, пов’язані з цими поняттями.

Дано:
\(P_{\text{середня}}=2\ \text{кВт}\)
\(t=2\ \text{год}\)
\(Q=24\ \text{МДж}\)

Знайти:
\(\text{ККД (%)}-?\)

У цій задачі ККД можна визначити як відношення виконаної тепловою машиною роботи \(A\) до отриманої нею енергії \(Q\): $$ \text{ККД}=\frac AQ\cdot 100\ \text{%}. $$

З умови задачі відомо, яку кількість теплоти отримала машина для її функціонування, а виконану нею роботу можна визначити за її потужністю: $$ P=\frac At, $$ де \(A\) – виконувана робота, а \(t\) – час її виконання.

Тоді роботу можна обчислити за формулою \(A=Pt.\)

Після переведення кіловат у вати, годин у секунди, а мегаджоулів у джоулі можна обчислити шуканий коефіцієнт корисної дії:

Відповідь: 60.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.

Дано:
\(R = 44\ \text{Ом}\)
\(\mathbf{\rho}=1,1\cdot 10^{-6}\ \text{Ом}\cdot \text{м}\)
\(S=1\ \text{мм}^2\)

Знайти:
\(l\ (\text{м})-?\)

Електричний опір \(R\) – фізична величина, яка характеризує властивість провідника протидіяти електричному струму.

Залежність опору провідника від його геометричних характеристик описують формулою $$ R=\mathbf{\rho}\frac lS, $$ де \(\mathbf{\rho}\) – питомий опір речовини, із якої виготовлено провідник; \(l\) – довжина провідника; \(S\) – площа поперечного перерізу провідника.

Після переведення міліметрів квадратних у метри квадратні можна обчислити шукану довжину дроту: $$ l=\frac{RS}{\mathbf{\rho}} =\frac{44\ \text{Ом}\cdot 0,000001\ \text{м}^2}{1,1\cdot 10^{-6}\ \text{Ом}\cdot \text{м}}=40\ \text{Ом}. $$

Відповідь: 40.

ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника.

Завдання скеровано на оцінювання вміння розв’язувати задачі на залежність періоду власних коливань системи від її параметрів.

Знайти:
\(l\ \text(м)-?\)

Математичний маятник – це фізична модель коливальної системи, яка складається з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля.

Характеристики коливань математичного маятника залежать від його довжини. Зокрема, можна визначити період коливань математичного маятника: $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) – довжина маятника; \(g\) – прискорення вільного падіння.

Період коливань – це час, за який коливання повністю повторюється.

За графіком коливань математичного маятника можна визначити період, вимірявши відстань між двома точками з однаковим положенням. Найпростіше визначити період між двома максимумами або мінімумами графіка. У цій задачі період коливань \(T\) дорівнює \(4\ \text{с}\) (рис. 1).

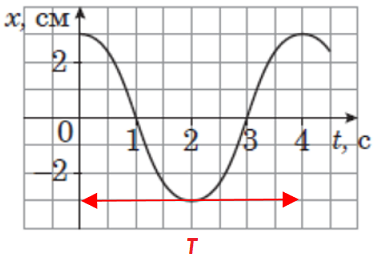
Рис. 1. Визначення періоду коливань

За допомогою періоду коливань можна виразити довжину маятника: $$ l=\frac{gT^2}{4\mathbf{\pi}^2}. $$

Оскільки за умовою \(\mathbf{\pi}^2=g,\) то $$ l=\frac{T^2}{4}=\frac{16}{4}=4\ (\text{м}). $$

Відповідь: 4.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіла під дією кількох сил.

Знайти:
\(\mathbf{\mu}-?\)

Розв’язання цієї задачі доцільно розпочати зі створення схеми дії сил на брусок, який тягнуть по рейці (рис. 1). На нього діють сила тяжіння \(m\overrightarrow{g}\) (перпендикуляно до поверхні землі вниз), сила реакції опори \(\overrightarrow{N}\) (перпендикулярно до поверхні рейки вгору), сила тертя \(\overrightarrow{F}_{\text{тертя}}\) (по всій поверхні контакту поверхні бруска в напрямку, протилежному до напрямку руху) і сила \(\overrightarrow{F},\) із якою брусок тягнуть по рейці (у напрямку руху).

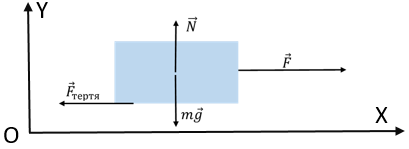
Рис. 1. Схема дії сил на брусок, що тягнуть по горизонтальній рейці

Другий закон Ньютона для бруска, що тягнуть по рейці, можна описати формулою $$ m\overrightarrow{a}=\overrightarrow{N}+m\overrightarrow{g}+\overrightarrow{F}_{\text{тертя}}+\overrightarrow{F}. $$

Оскільки брусок тягнуть рівномірно, то прискорення \(\overrightarrow{a}=0.\) Тоді $$ \overrightarrow{N}+m\overrightarrow{g}+\overrightarrow{F}_{\text{тертя}}+\overrightarrow{F}=0. $$

Затим потрібно спроєктувати рівняння на осі \(OX\) й \(OY,\) скориставшись рисунком 1:

проєкція на вісь \(OX:\ 0+0-F_{\text{тертя}}+F=0;\)

проєкція на вісь \(OY:\ N-mg+0+0=0.\)

Тобто для осі \(OX \ F_{\text{тертя}}=F,\) для осі \(OY\ N=mg.\)

Величина сили тертя залежить від коефіцієнта тертя: $$ \overrightarrow{F}_{\text{тертя}}=-\mathbf{\mu}\overrightarrow{N}, $$ де знак «мінус» показує, що сила тертя діє проти напрямку руху.

Тож $$ F=\mathbf{\mu}N=\mathbf{\mu}mg,\ \mathbf{\mu}=\frac{F}{mg}. $$

При цьому силу \(F\) можна визначити за показами динамометра, зображеного на рисунку, де брусок тягнуть горизонтально: $$ F=0,9\ \text{H}. $$

Оскільки для тіла в стані спокою можна обчислити вагу \(\overrightarrow{P},\) то значення \(mg\) можна визначити за показанням динамометра під час зважування бруска: $$ \overrightarrow{P}=m\overrightarrow{g},\ \ mg=3,6\ \text{H}. $$

Тоді $$ \mathbf{\mu}=\frac{F}{mg}=\frac{0,9\ \text{H}}{3,6\ \text{H}}=0,25. $$

Відповідь: 0,25.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція, Закон електромагнітної індукції.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на застосування закону електромагнітної індукції.

Дано:
\(\triangle\mathbf{\Phi}=20\ \text{мВб}\)
\(R=0,04\ \text{Ом}\)

Знайти:
\(q\ (\text{Кл})-?\)

Заряд проходить через виток під час зміни магнітного потоку, бо за законами електромагнітної індукції в такому разі утвориться струм. Цей струм сприятиме виникненню власного магнітного поля витка, що протидіятиме зміні потоку крізь нього. Такий струм називають індукційним. Силу індукційного струму визначають за формулою $$ I=\frac{\mathbf{\varepsilon}_l}{R}, $$ де \(\mathbf{\varepsilon}_l\) – електрорушійна сила (ЕРС) індукції.

За законом електромагнітної індукції ЕРС індукції дорівнює швидкості зміни магнітного потоку, який пронизує поверхню, обмежену контуром. Тобто $$ \mathbf{\varepsilon}_l=-\frac{\triangle\mathbf{\Phi}}{\triangle t}, $$ де \(\triangle t\) – час, за який відбуваються зміни магнітного потоку. Знак «мінус» у цьому виразі показує, що ЕРС самоіндукції утворюється, щоби протистояти (правило Ленца) зміні магнітного потоку. Тоді $$ I= \frac{\triangle\mathbf{\Phi}}{\triangle t\cdot R}. $$

За визначенням сила струму – це фізична величина, яка характеризує електричний струм. Її описують формулою $$ I=\frac{q}{\triangle t}, $$ де \(q\) – це заряд, що проходить через поперечний переріз провідника, а \(\triangle t\) – проміжок часу, за який це відбувається.

Тоді $$ \frac{q}{\triangle t}=\frac{\triangle\mathbf{\Phi}}{\triangle t\cdot R}, $$ a

Відповідь: 0,5.

ТЕМА: Електромагнітні коливання і хвилі. Власна частота та період електромагнітних коливань. Формула Томсона. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).

Завдання скеровано на оцінювання вміння розв’язувати комбіновані задачі з використанням формули Томсона й на зв’язок між періодом, швидкістю поширення і довжиною хвилі.

Дано:
\(L=25\ \text{мкГн}\)
\(C=3600\ \text{пФ}\)
\(c=3\cdot 10^8\ \text{м/с}\)
\(\mathbf{\pi}=3,1\)

Знайти:
\(\mathbf{\lambda}\ (\text{м})-?\)

За ємністю конденсатора й індуктивністю котушки коливального контуру можна визначити період \(T\) коливань, які виникають під час роботи конденсатора: $$ T=2\mathbf{\pi}\sqrt{LC}. $$

Період коливань – це час, за який коливання повністю повторюється.

Довжина хвилі \(\mathbf{\lambda}\) – це відстань між двома найближчими точками, які коливаються синхронно.

Тобто за один період частинка переміститься на довжину хвилі, тому можна записати таке співвідношення для цих величин: $$ \mathbf{\lambda}=Tv, $$ де \(v\) – швидкість поширення хвилі.

Електромагнітні хвилі поширюються зі швидкістю світла, тому можемо уточнити цей вираз:

Відповідь: 558.

ТЕМА: Оптика. Оптична сила лінзи. Формула тонкої лінзи.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на формулу тонкої лінзи.

Дано:
\(D=1,5\ \text{дптр}\)
\(H=3\ \text{м}\)

Знайти:
\(d\ (\text{м})-?\)

Оптичну силу лінзи і її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи: $$ d=\frac 1d+\frac 1f, $$ де \(d\) – відстань від об’єкта до лінзи, а \(f\) – відстань від лінзи до зображення (рис. 1).

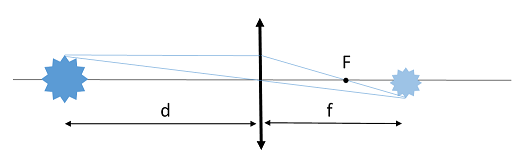
Рис. 1. Схема ходу променів крізь тонку лінзу

За умовою потрібно отримати зображення на відстані 3 м від світильника, тобто \(d+f=H,\) відповідно \(f=H\ –\ d,\) а $$ D =\frac 1d+\frac{1}{H-d}. $$

Отже \begin{gather*} \frac{H-d+d}{d(H-d)}=\frac{H}{d(H-d)}=D,\\[6pt] H=dD(H-d),\\[7pt] H=dDH-d^2 D,\\[7pt] d^2 D-dDH+H=0. \end{gather*}

Затим потрібно підставити всі відомі величини й розв’язати отримане внаслідок перетворень рівняння відносно \(d\): $$ 1,5d^2-4,5 d+3=0,\ \ d^2-3d+2=0. $$

Дискримінант \(D=(-3)^2-4\cdot 1\cdot 2=1,\) тож $$ d_1=\frac{3-\sqrt{1}}{2\cdot 1}=1\ \ \text{і}\ \ d_2=\frac{3+\sqrt{1}}{2\cdot 1}=2. $$

Умову задачі задовольняє менше значення \(d=1.\)

Відповідь: 1.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на обчислення червоної межі фотоефекту.

Дано:
\(A_{\text{вих}}=4,5\ \text{еВ}\)
\(1\ \text{еВ}=1,6\cdot 10^{-19}\ \text{Дж}\)
\(h=6,6\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\)
\(c=3\cdot 10^8\ \text{м/с}\)

Знайти:
\(\mathbf{\lambda}_{\text{гранична}}\ (\text{м})-?\)

Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.

Частинки світла (фотони) під час зустрічі з катодом передають енергію електронам на його поверхні. Енергію рухомого фотона визначають за формулою \(E=hv,\) де \(E\) – енергія фотона, \(v\) – частота випромінювання.

Енергію \(E\), отриману від фотона, електрон витрачає на те, щоби вирватися з поверхні металу (робота виходу \(A_{\text{вих}}\)) і на його рух після цього (кінетична енергія \(E_{\text{кін}}\): $$ E = A_{\text{вих}}+E_{\text{кін}}. $$

Мінімальна енергія, яку потрібно передати електронам, щоби фотоефект відбувався дорівнює роботі виходу: $$ E = A_{\text{вих}}+hv_{\text{гранична}}. $$

Між частотою випромінювання і довжиною хвилі випромінювання є зв’язок: $$ v=\frac{c}{\mathbf{\lambda}} $$

Тому

Відповідь: 275.