ЗНО онлайн 2021 року з фізики – пробний тест

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на перевірку вміння працювати зі шкалами вимірювальних пристроїв і визначати ціну поділки шкали.

Для того щоби визначити ціну поділки секундоміра, потрібно вибрати дві поділки, значення яких відомі. Шкала секундоміра розрахована на 60 с. Тож цифри, зображені на шкалі поруч із великими поділками, відповідають часу, виміряному в секундах (5 с, 10 с, 15 с тощо).

Ціна великої поділки дорівнює різниці між двома послідовними великими поділками (позначено червоним кольором на рисунку 1): $$ 10\ \text{с}-5\ \text{с}=5\ \text{с}. $$

Рис. 1. Дві послідовні великі поділки на шкалі та п’ять середніх поділок між ними

Між двома послідовними великими поділками є п’ять середніх поділок (позначено синім кольором на рис. 1). Між двома сусідніми середніми поділками є п’ять поділок, ціну яких потрібно визначити. Тобто між двома великими поділками розташовано 25 маленьких. Ціну маленької поділки можна обчислити як частку від ділення ціни великої поділки на кількість маленьких поділок на ній: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=\frac{5\ \text{с}}{25}=0,2\ \text{с}. $$

Відповідь: Б.

ТЕМА: Механіка. Основа динаміки. Додавання сил.

Завдання скеровано на оцінювання розуміння поняття рівнодійної.

Якщо рівнодійна сил, що діють на тіло, дорівнює нулю, то тіло перебуває у стані спокою. Тіло у стані спокою має постійну швидкість.

Адже за другим законом Ньютона $$ \overline{F}=m\overline{a}, $$ де \(\overline{F}\) – рівнодійна, \(m\) – маса тіла, \(\overline{a}\) – прискорення тіла.

Якщо тіло не рухається, можна вважати, що його швидкість постійна й дорівнює 0 м/с.

У варіанті відповіді А віз залишається на своєму місці, а в Б вода у склянці нерухома, тож їхні швидкості дорівнюють нулю. А отже й рівнодійна сил, що діють на них, – теж.

У варіанті відповіді В парашутист рухається рівномірно вниз, тобто його швидкість постійна, а отже й рівнодійна, що діє на нього, дорівнює нулю.

У варіанті відповіді Г літак щойно відірвався від злітно-посадкової смуги. Тобто він лише почав набирати швидкість і рухався із прискоренням. Тож рівнодійна сил, що діють на нього, не дорівнює нулю.

Відповідь: Г.

ТЕМА: Основи молекулярно-кінетичної теорії. Маса й розмір молекул.

Завдання скеровано на оцінку розуміння відмінності між фізичними й хімічними явищами в молекулярній фізиці.

Під час зміни макроскопічних параметрів (температури, об’єму чи тиску) хімічний склад речовини не змінюється. Молекули – це найменші частинки речовини, носії її хімічних властивостей.

Тому, якщо хімічний склад речовини не змінюється, то й самі молекули також не змінюються.

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.

Опір провідника залежить від його геометричних характеристик: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – питомий опір речовини, iз якої виготовлений провідник, \(l\) – довжина провідника, \(S\) – площа поперечного перерізу провідника.

Опір провідника не зміниться, якщо не змінюється його довжина чи площа поперечного перерізу.

У варіанті відповіді А довжина провідника зменшиться вдвічі, а поперечний переріз збільшиться вдвічі, якщо розрізати його навпіл і з’єднати половинки паралельно. Тож опір провідника зменшиться: $$ R_A=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac {l/2}{2S}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{4S}=\frac 14 R. $$

У варіанті відповіді Б довжина провідника збільшиться. Під час видовження площа поперечного перерізу зменшиться. А тому опір провідника збільшиться.

У варіанті відповіді В під час нарізання різьби на провіднику зменшиться площа його поперечного перерізу, а опір, відповідно, збільшиться.

Лише у варіанті відповіді Г не змінюються геометричні характеристики провідника. Доданий зовні ізолювальний шар не впливає на його опір.

Відповідь: Г.

ТЕМА: Оптика. Джерела світла.

Завдання скеровано на оцінку розуміння поняття джерела світла.

Місяць – це кам’яний супутник Землі. Подібно до інших планет і супутників він не може бути джерелом світла, тобто випромінювати частинки світла (фотони). Він лише відбиває сонячне випромінювання.

Відповідь: B.

ТЕМА: Механіка. Умови рівноваги. Прості механізми.

Завдання скеровано на оцінку розуміння принципів роботи простих механізмів, зокрема рухомого й нерухомого блоків.

Нерухомий блок (рис. 1, а) не дає виграшу в силі – він дає змогу змінити лише напрямок прикладання сили, тобто $$ |\overline{F_1}|=|\overline{F_2}|. $$

Рухомий блок (рис. 1, б) дає виграш у силі у 2 рази. Тобто сила, необхідна для піднімання вантажів за допомогою рухомого блоку, буде вдвічі менша, ніж якщо вантаж піднімати без використання механізмів: $$ |\overline{F_1}|=\frac{|\overline{F_2}|}{2}. $$

Тож виграш у силі в системі залежить лише від кількості рухомих блоків.

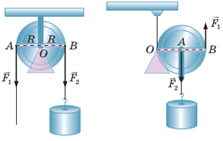
Рис. 1. а) Нерухомий блок, б) рухомий блок

Тоді нехай сила \(\overline{F}\) – це сила, яка необхідна для того, щоби підняти вантаж без будь-яких механізмів.

Тоді після першого рухомого блоку виграш у силі дорівнюватиме 2: $$ |\overline{F_1}|=\frac{|\overline{F}|}{2}. $$

Другий рухомий блок знову даватиме виграш у силі у 2 рази відносно попереднього блоку, а отже виграш у силі – у 4 рази відносно переміщення вантажу без механізмів: $$ |\overline{F_2}|=\frac{|\overline{F_1}|}{2}=\frac{|\overline{F}|}{4}. $$

Третій рухомий блок дає виграш у силі уже у 8 разів відносно переміщення вантажу без механізмів: $$ |\overline{F_3}|=\frac{|\overline{F_2}|}{2}=\frac{|\overline{F_1}|}{4}=\frac{|\overline{F}|}{8}. $$

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.

Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі з визначення роботи сил.

Якщо тіло зісковзує по площині рівномірно, то його прискорення \(\overline{a}\) дорівнює нулю. Тоді за другим законом Ньютона $$ \overline{F}=m\overline{a}=0, $$ де \(\overline{F}\) – рівнодійна, \(m\) – маса тіла, \(\overline{a}\) – прискорення тіла.

Рівнодійна сил, які діють на тіло, що рухається по похилій площині (рис. 1), дорівнює векторній сумі всіх цих сил: $$ \overline{F}=\overline{F_{\text{тяж}}} +\overline{F_{\text{тер}}}+\overline{N}=0. $$

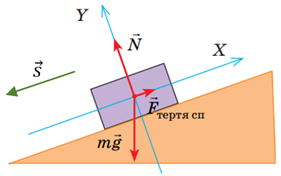
Рис. 1. Схематичне зображення сил, що діють на тіло на похилій площині

Це рівняння можна спроєктувати на осі \(OX\) і \(OY\) відповідно. Напрямок осей вибрано як на рисунку 1: \begin{gather*} F_x=-F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+F_{\text{тер}}=0;\\[7pt] F_y=-F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+N=0, \end{gather*} де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут нахилу похилої площини.

Тож \begin{gather*} F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=F_{\text{тер}};\\[7pt] F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=N. \end{gather*}

Силу тертя визначають за формулою $$ F_{\text{тер}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}N. $$

Тож \begin{gather*} F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}N=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha};\\[7pt] \sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. \end{gather*}

Роботу сили можна обчислити за формулою $$ A=Fs\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}, $$ де \(F\) – сила, що діє на тіло, \(s\) – переміщення тіла, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – кут між напрямками векторів сили й переміщення.

Тоді можна записати роботу сили тяжіння і сили тертя. Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) між напрямком сили тяжіння і переміщення \(s\) дорівнює \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=90-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\), тож можна скористатися тригонометричними формулами зведення: \begin{gather*} A_{\text{тяж}}=F_{\text{тяж}}s\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=F_{\text{тяж}}s\cos(90-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha})=\\[7pt] =F_{\text{тяж}}s\sin(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}). \end{gather*}

Кут між напрямком сили тертя і переміщенням \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=180^\circ\), тож \begin{gather*} A_{\text{тер}}=F_{\text{тер}}s\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=-F_{\text{тер}}s=\\[7pt] =-F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}s. \end{gather*}

Оскільки модуль сили тяжіння і переміщення додатні, а \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – це кут, менший за \(90^\circ\), синус якого більший за нуль, можна зробити висновок: $$ A_{\text{тяж}}=-A_{\text{тер}}\gt 0. $$

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на перевірку розуміння природи кінетичної енергії.

Кінетичну енергію обчислюють за формулою $$ E_k=\frac{mV^2}{2}, $$ де \(m\) – маса тіла, а \(V\) – швидкість його руху.

Тож кінетична енергія тіла змінюється, якщо змінюється його швидкість або маса.

У варіанті відповіді А пліт рухається ділянкою річки, що має сталі ширину й глибину. Швидкість такої течії залишається сталою. Пліт не має власної швидкості, тож якщо швидкість течії не змінюється, то й кінетична енергія плота не змінюється.

У варіанті відповіді Б м’яч закидають у баскетбольний кошик. Щоби потрапити в кошик, м’яч має рухатися по параболі (рис. 1). Модуль швидкості м’яча спочатку зменшується, у найвищій точці траєкторії він дорівнює нулю, після чого знову поступово збільшується. Якщо модуль швидкості м’яча змінюється, то і його кінетична енергія також змінюється.

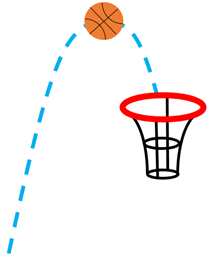
Рис. 1. Траєкторія руху м’яча

У варіанті відповіді В листочок рухається рівномірно, тож його швидкість і кінетична енергія не змінюються.

У варіанті відповіді Г равлик рухається зі сталою швидкістю – 9 см/хв, тож кінетична енергія також не змінюється.

Відповідь: Б.

ТЕМА: Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл.

Завдання скеровано на перевірку розуміння механізмів кристалізації і конденсації.

Хмари утворюються завдяки тому, що тепле повітря має меншу густину, ніж холодне, тож воно швидко піднімається вгору. У вищих шарах атмосфери повітря адіабатно розширюється, що приводить до його охолодження.

Зі зниженням температури максимальна кількість води, яку може втримувати повітря, зменшується. Тож водяна пара в повітрі, що швидко охолодилося під час піднімання, конденсується і утворюються крапельки води, із яких і складаються хмари.

За такої конденсації в хмарах майже немає пилинок чи інших частинок, які можуть стати центрами кристалізації. У такому разі рідина кристалізується за значно нижчих температур.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння користуватися графіками для визначення макроскопічних параметрів газу й використовувати це для розв’язування розрахункових задач.

Температура \(T\), тиск \(p\) й об’єм \(V\) пов’язані рівнянням стану ідеального газу $$ pV=nRT, $$ де \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

Тож тиск можна визначити за значеннями об’єму й температури. Оскільки кількість речовини \(n=1\ \text{моль}\), то тиск для ідеального газу $$ p=\frac{RT}{V}. $$

Масштаб на графіках невідомий, тому точно тиск визначити неможливо, але можна порівняти його в різних варіантах, прийнявши, що клітинка вздовж осі \(T\) дорівнює умовній одиниці температури (у. о. т.), а вздовж осі \(V\) – умовній одиниці об’єму (у. о. о.). Тиск у такому разі вимірюють в умовних одиницях тиску (у. о.).

Можна визначити об’єм і температуру для варіантів відповіді, поданих у завданні:

Після цього можна розрахувати тиск:

Тож найвищий тиск у точці B.

Відповідь: B.

ТЕМА: Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку розуміння понять температури плавлення, питомої теплоємності й питомої теплоти плавлення речовин.

Для того щоби розплавити метал в алюмінієвій посудині, температура його плавлення має бути меншою, ніж в алюмінію. Адже саме посудина передаватиме теплоту до металу всередині, а теплота може самовільно передаватися лише від більш нагрітого тіла до менш нагрітого.

Тож в таблиці треба вибрати метал із меншою температурою плавлення, ніж алюміній, тобто свинець.

Відповідь: Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Поняття про плазму.

Завдання скеровано на перевірку розуміння поняття плазми.

Пригадаймо, що плазма – це частково або повністю йонізований газ, у якому концентрації позитивних і негативних зарядів майже однакові. Під час йонізації нейтральні атоми газу втрачають електрони й перетворюються на позитивні йони. Тож вільними носіями в плазмі є як утворені вільні електрони, так і позитивні йони.

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.

Завдання скеровано на оцінку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.

За правилом правої руки можна визначити напрямок ліній магнітної індукції.

Якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом.

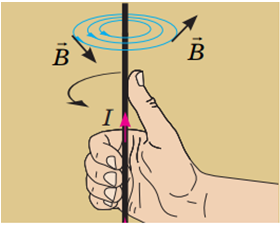
Рис. 1. Правило правої руки

Тож, як зображено на рисунку, якщо сила струму напрямлена вгору, то лінії магнітної індукції утворюють коло навколо провідника, і вектор магнітної індукції спрямований праворуч у точці кола, найближчій до спостерігача.

Відповідь: B.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку розуміння поняття термоелектронної емісії.

Термоелектронна емісія – це явище випромінювання електронів нагрітими тілами. Що вища температура тіла, то більша швидкість електронів, які покидають його поверхню.

Відповідь: Г.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на перевірку розуміння базових понять, що стосуються механічних коливань.

А Швидкість світла в повітрі близька до швидкості світла у вакуумі \((3\cdot 10^8\ \text{м/с})\) , а швидкість звуку в повітрі становить \(343\ \text{м/с}\), тому швидкість світла набагато більша за швидкість звуку, а не навпаки.

Б Вимушені коливання – це коливання, які відбуваються в системі внаслідок дії зовнішньої сили, що періодично змінюється. Між двома торканнями на струни не діє жодна зовнішня сила, тому в цьому разі коливання є вільними.

В Звук – це поздовжня механічна хвиля. Механічні хвилі можуть поширюватися лише в середовищі. У відкритому космосі немає атмосфери, у якій би міг поширюватися звук, тому єдиний спосіб комунікації – це електромагнітні хвилі, які можуть поширюватись у вакуумі. Радіохвилі – це електромагнітні хвилі із частотою меншою, ніж \(3\ 000\ \text{ГГц}\). Тож якщо в космонавтів відмовить радіозв’язок, то вони не зможуть розмовляти.

Г Збіг власної частоти коливання крил і частоти коливання повітряних потоків приведе до резонансу. Резонанс – це явище різкого збільшення амплітуди, яке виникає, якщо частота зовнішньої сили, що періодично змінюється, збігається із власною частотою коливань системи. Кріплення крил літака можуть не витримати різкого збільшення амплітуди коливань і зруйнуватися.

Тож твердження Г – правильне.

Відповідь: Г.

ТЕМА: Оптика. Закони відбивання світла. Закони заломлення світла. Лінза.

Завдання скеровано на перевірку розуміння принципів роботи оптичних елементів.

Промені проходять крізь склянку з водою, адже в іншому разі неможливо було би побачити Гаррі, що розташований за нею. Тому склянка з водою не виконує функцію дзеркала. З тієї самої причини склянка не змінює хід променів на зворотний.

Після наповнення склянки водою утворюється дійсне перевернуте зображення Гаррі. Розсіювальна лінза утворює лише уявне пряме зменшене зображення. Збиральна ж лінза може утворювати дійсне перевернуте зображення, що має ті самі розміри, що і предмет, якщо він перебуває на відстані від лінзи, яка дорівнює її подвійному фокусу.

Відповідь: А.

ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на оцінку розуміння постулатів спеціальної теорії відносності.

Щоби порівняти час, виміряний у рухомій і нерухомій системах, потрібно пригадати, як їх визначають.

Рухома система координат прив’язана до тіла, що рухається. У ній спостерігач рухається разом із тілом, як, наприклад, пасажир усередині ракети. Для такого спостерігача тіло і світловий годинник, який вимірює час, не рухається.

У нерухомій системі координат спостерігач стежить за рухомим тілом, як, наприклад, людина, що залишається на Землі, коли ракета пролітає в небі. У такому разі світловий годинник рухається.

За спеціальною теорією відносності швидкість світла у вакуумі має однакові значення в усіх системах відліку. Тож, щоби швидкість світла в рухомій і нерухомій системі відліку могла бути однаковою, час у них має текти по-різному. Час, виміряний у рухомій системі координат, має бути меншим, ніж виміряний у нерухомій системі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}_0}{\sqrt{1-\frac{v^2}{c^2}}}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}_0\) – час, виміряний у рухомій системі координат, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}\) – час, виміряний у нерухомій систем координат (у цій системі координат спостерігач бачить рух тіла ззовні).

Відповідь: Г.

ТЕМА: Квантова фізика. Світлові кванти.

Завдання скеровано на оцінювання розуміння зв’язку між корпускулярними і хвильовими властивостями світла.

Енергія фотона пов’язана з його довжиною хвилі: $$ E=\frac{hc}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}, $$ де \(h\) – стала Планка, \(c\) – швидкість світла у вакуумі, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) – довжина хвилі випромінювання.

Тож довжину хвилі випромінювання можна визначити за формулою:

Світло видимого діапазону має довжину хвилі від \(380\ \text{нм}\) до \(740\ \text{нм}\). Ультрафіолетове випромінювання має меншу довжину хвилі, ніж видиме \((10\ \text{нм}\ –\ 380\ \text{нм})\), рентгенівське випромінювання – меншу, ніж ультрафіолетове \((5\ \text{пм}\ –\ 10\ \text{нм})\). Інфрачервоне випромінювання має більшу довжину хвилі, ніж видиме \((740\ \text{нм}\ –\ 1\ \text{мм})\).

Тож електромагнітне випромінювання, про яке йдеться в завданні, – видиме.

Відповідь: B.

ТЕМА: Квантова фізика. Атом і атомне ядро.

Завдання скеровано на перевірку розуміння будови атома й уміння інтерпретувати рівняння ядерних реакцій.

Атом складається із позитивно зарядженого ядра й негативно заряджених електронів. Ядро ж складається із частинок двох видів – позитивно заряджених протонів і нейтральних нейтронів. Заряди протона й електрона однакові за модулем. Атом – це нейтральна частинка, тому кількість електронів у ньому дорівнює кількості протонів. Кількість нейтронів може відрізнятися від кількості протонів чи електронів.

Для того, щоб описати нуклон, поруч із хімічним символом елемента зазначають лівий надрядковий індекс – кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів) – і лівий підрядковий індекс – кількість протонів.

Оскільки в атомі зарядженими частинками є електрони й протони, кількість яких однакова, то сумарна кількість заряджених частинок дорівнює $$ 30\cdot 2=60. $$

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на оцінку розуміння фізичних понять, що стосуються рівномірного руху по колу.

Переміщення – це векторна величина, яку графічно подають у вигляді напрямленого відрізка прямої, який з’єднує початкове й кінцеве положення матеріальної точки.

Шлях – це фізична величина, що чисельно дорівнює довжині траєкторії руху матеріальної точки за певний інтервал часу.

Швидкість – це векторна фізична величина, яка дорівнює відношенню переміщення \(s\) до інтервалу часу \(t\), за який це переміщення відбулося: $$ \overline{v}=\frac{\overline{s}}{t}. $$

Кутова швидкість – це фізична величина, яка чисельно дорівнює куту повороту \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) радіуса за час \(t\): $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}}{t}. $$

Під час переміщення з точки 1 у точку 2 тіло пройшло півкола, тобто \(180^\circ\) чи \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\ \text{рад}\). У такому разі модуль переміщення, тобто відстань між початковою і кінцевою точкою, дорівнює \(2R\).

Шлях у цьому випадку – це довжина дуги, яку пройшло тіло. Її можна розрахувати за формулою: $$ l=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R\cdot\frac {\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R\cdot\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R. $$

Модуль швидкості можна розрахувати, якщо модуль переміщення \(s\) поділити на \(t\): $$ v=\frac st=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R}{t}. $$

Кутову швидкість можна розрахувати за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}}{t}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{t}. $$

Відповідь: 1Г, 2В, 3Б, 4А.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку розуміння будови речовин у різних агрегатних станах.

1. У рідинах молекули перебувають одна від одної на відстані, що приблизно дорівнює їхньому розміру. На таких відстанях сили відштовхування і притягання, що виникають між молекулами, урівноважують одні одних. Якщо молекули спробувати зблизити, то сили відштовхування переважатимуть над силами притягання і навпаки. Саме тому зменшити об’єм рідини так складно. Тож м’яч, заповнений водою, неможливо стиснути, бо між молекулами рідини діють сили відштовхування.

2. Люди відчувають запах тої чи тої речовини, бо її молекули потрапляють на рецептори в носі. Запах свіжої випічки поширюється в повітрі завдяки дифузії молекул запашних речовин у повітрі. Дифузія – процес взаємного проникнення молекул однієї речовини між молекулами іншої, який відбувається внаслідок теплового руху цих молекул.

3. Хоча молекули рідин і перебувають одна від одної на відстанях, що приблизно дорівнюють їхнім розмірам, але вони не утворюють чіткої структури на відміну від твердих тіл. Між молекулами є невеликі проміжки, які і займають атоми чи молекули розчинених речовин, наприклад, цукру. Оскільки ці молекули зазвичай займають проміжки, що й так існували між молекулами рідини, то після розчинення об’єм рідини загалом майже не змінюється.

4. Сили притягання також діють між молекулами твердих тіл, якщо вони перебувають достатньо близько одна від одної. Тому, якщо під час тертя скло і дзеркальце зможуть бути у прямому контакті, то між їхніми молекулами почнуть діяти сили притягання, унаслідок чого дзеркальце прилипне до віконного скла.

Відповідь: 1А, 2Д, 3Б, 4Г.

ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.

Завдання скеровано на перевірку розуміння фізичних величин, пов’язаних із механічними коливаннями.

1. Потенціальна енергія тіла, що здійснює коливання на пружині (зокрема горизонтальні), залежить від жорсткості пружини і її абсолютного видовження: $$ E_{\text{пот}}=\frac{kx^2}{2}. $$

2. Період коливань математичного маятника залежить лише від його довжини й прискорення вільного падіння: $$ T_{\text{мат}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac lg}. $$

3. Кінетична енергія тіла (зокрема того, що коливається), залежить від його швидкості й маси: $$ E_{\text{кін}}=\frac{mv^2}{2}. $$

4. Період коливання тіла, що здійснює коливання на пружин, і залежить від жорсткості пружини й маси тіла: $$ T_{\text{пруж}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac mk}. $$

Відповідь: 1А, 2Д, 3Г, 4Б.

ТЕМА: Атом і атомне ядро.

Завдання скероване на перевірку розуміння історично важливих фізичних експериментів і вміння пов’язувати їх із фізичними відкриттями.

1. Анрі Беккерель проводив дослідження із використанням солей Урану й випадково поклав породу разом із фотопластинкою в темну шухляду. Наступного разу, коли він повернувся до фотопластинок, вони виявилися засвіченими, хоча ніяких джерел світла в шухляді не було. Так у нього виникла ідея про те, що саме Уран був джерелом якогось випромінювання. Це випромінювання і було радіоактивним випромінюванням, що утворювалось під час розпаду нестабільних ядер Урану.

2. Планетарну модель атома розробив Ернест Резерфорд після того, як експеримент із перевірки пудингової моделі Томсона мав неочікувані результати. За уявленнями Томсона позитивний заряд в атомі займав увесь його об’єм, як тісто в пудингу чи кексі, а негативно заряджені електрони застрягали в цьому позитивному заряді (як родзинки). Якщо атом і справді мав таку будову, то під час зустрічі з ним інші (менші) частинки мали би пролітати наскрізь. Адже самі електрони мали би занадто малу масу, щоби викликати якусь серйозну зміну траєкторії, а хмара позитивного заряду могла спричинити відхилення лише на невеликі кути. Щоби перевірити це експериментально, Резерфорд бомбардував альфа-частинками тонку фольгу золота, товщина якої становила лише кілька атомів. Деякі альфа-частинки відбивалися від фольги майже у протилежному напрямку. Таке відбивання було можливе лише за умови, що в атомі існувала велика важка частинка. Тож Резерфорд припустив, що атом більше схожий на Сонячну систему, ніж на пудинг: у його центрі є велика позитивна частинка – ядро, навколо якого обертаються електрони, як планети навколо Сонця.

3. Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів. Закони фотоефекту були відкриті під час опромінення металів світлом.

4. α-промені – це потік позитивно заряджених частинок, що складаються із двох протонів і двох нейтронів (ядра атомів Гелію), β-промені – це потік негативно заряджених електронів, γ-промені – це електромагнітне випромінювання надзвичайно високої частоти, що утворюється під час ядерних реакцій. Ернест Резерфорд виявив, що під дією магнітного поля пучок радіоактивного випромінювання ділиться на три частини. Поділ відбувається тому, що під дією магнітного поля заряджені частинки відхиляються від своєї початкової прямолінійної траєкторії. Нейтральний γ-промінь не відхилявся під дією магнітного поля, а позитивно заряджені α-частинки й негативно заряджені β-частинки відхилялися й утворювали два пучки по обидва боки від пучка γ-променів. Адже різнойменно заряджені частинки в магнітному полі відхиляються у протилежні боки.

Відповідь: 1Г, 2А, 3В, 4Б.

ТЕМА: Механічні коливання і хвилі. Звукові хвилі. Ехолокація.

Завдання скеровано на оцінку розуміння принципів ехолокації і вміння розв’язувати відповідні розрахункові задачі.

Дано:
\(l=170\ \text{м}\)
\(c\ (\text{звуку})=340\ \text{м/с}\)
\(v\ (\text{кажана})=20\ \text{м/с}\)

1. Знайти:
\(t\ (\text{с})\ -\ ?\)

Звук – це механічна хвиля, що має частоту \(20\ –\ 20\ 000\ \text{Гц}\). Кажан, що випустив ультразвуковий сигнал, не має впливу на швидкість поширення цього сигналу в середовищі, тому можна визначити час, який знадобиться сигналу для того, щоби досягти перепони з визначення швидкості: \begin{gather*} c\ (\text{звуку})=\frac lt\rightarrow \\[6pt] t=\frac{l}{c\ (\text{звуку})}=\frac{170\ \text{м}}{340\ \text{м/с}}=0,5\ \text{с}. \end{gather*}

2. Знайти:
\(l'\ (\text{м})\ -\ ?\)

Нехай кажан отримає зворотний сигнал на відстані \(l'\) від перепони в момент часу \(t'\). Тоді за цей час звукова хвиля пройде відстань від кажана в початковій точці до перепони \(l\) і відстань від перепони до кажана \(l'\): $$ l_{\text{звуку}}=l+l'. $$

Кажан пройде відстань, що дорівнює різниці початкової і кінцевої відстані до перепони: $$ l_{\text{кажана}}=l-l'. $$

Кажан і звукова хвиля долають відповідні відстані за однаковий час, тому:

Відповідь: 1. 0,5. 2. 151.

ТЕМА: Теплота згоряння палива. Рівняння теплового балансу палива. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з рівняннями теплового балансу.

1. Дано:
\(V=4\cdot 10^8\ \text{м}^3\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=1\ \frac{\text{кг}}{\text{м}^3}\)
\(q=40\ \text{МДж/кг}\)

1. Знайти:
\(Q\ (\text{Дж})\ -\ ?\)

Кількість теплоти, що виділяється під час згоряння палива, можна розрахувати за формулою: $$ Q=qm, $$ де \(q\) – питома теплота згорання палива, \(m\) – маса палива.

Маса палива пов’язана з його об’ємом \(V\) й густиною \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\): $$ m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V. $$

Тож можна розрахувати виділену кількість теплоти:

2. Дано:
\(m_{\text{пов}}=8\cdot 10^{13}\ \text{кг}\)
\(c_{\text{пов}}=1000\ \frac{\text{Дж}}{\text{кг}\ \cdot\ ^\circ\mathrm{C}}\)
\(q=40\ \text{МДж/кг}\)

2. Знайти:
\(\triangle t\ (^\circ\mathrm{C})\ -\ ?\)

Для того, щоб оцінити, як зміниться температура тропосфери, потрібно записати рівняння теплового балансу $$ Q=cm\triangle t, $$ де \(Q\) – отримана (або віддана) кількість теплоти, \(c\) – питома теплоємність тіла, \(m\) – маса тіла. \(\triangle t\) – зміна температури тіла.

Якщо кількість теплоти \(Q=16\ \text{ПДж}\) повністю передається тропосфері, то саме ця \(Q\) є отриманою кількість теплоти в лівій частині рівняння теплового балансу. Тож можна розрахувати зміну температури:

Відповідь: 1. 16. 2. 0,2.

ТЕМА: Основи динаміки. Другий закон Ньютона. Основи електростатики. Закон Кулона.

Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі, пов’язані із силою Кулона.

1. Дано:
\(T_1=1\ \text{мН}\)
\(T_2=1,5\ \text{мН}\)

1. Знайти:
\(F\ (\text{мН})\ -\ ?\)

Спочатку на кульку діяли лише сили натягу підвісу й сила тяжіння (рис. 1, а). Кулька перебуває у стані спокою, тому рівнодійна цих сил дорівнює 0: $$ \overrightarrow{F}=\overrightarrow{T_1}+m\overrightarrow{g}=0. $$

Цей векторний вираз можна спроєктувати на вертикальну вісь: \begin{gather*} T_1-mg=0;\\[7pt] T_1=mg. \end{gather*}

Після того, як до першої кульки наблизили другу, окрім сили натягу підвісу й сили тяжіння на кульку діє сила Кулона (рис. 1, б). Але навіть у такому разі тіло перебуває у стані спокою, тобто рівнодійна цих сил дорівнює нулю: $$ \overrightarrow{F}=\overrightarrow{T_2}+m\overrightarrow{g}+\overrightarrow{F_{\text{Кл}}}=0. $$

Цей векторний вираз можна спроєктувати на вертикальну вісь: $$ T_2-mg-F_{\text{Кл}}=0. $$

Зважаючи на те, що \(T_1=mg\), можна розрахувати силу Кулона: $$ F_{\text{Кл}}=T_2-T_1=1\ \text{мН}-1\ \text{мН}=0,5\ \text{мН}. $$

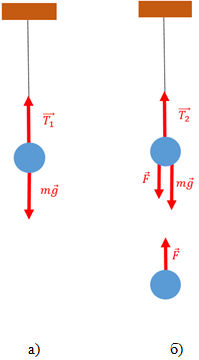
Рис. 1. Схематичне зображення сил: а) для одної кульки, б) для двох кульок

2. Дано:
\(r_1=\frac{r_1}{2}\)

2. Знайти:
\(T_3\ (\text{мН})\ -\ ?\)

Силу Кулона визначають за формулою $$ F=k\frac{|q_1||q_2|}{r^2}. $$

Тоді можна записати силу взаємодії до того, як кульки наблизили одну до одної: $$ F_{\text{Кл1}}=k\frac{|q_1||q_2|}{r^2_1}. $$

Ця сила взаємодії дорівнює \(0,5\ \text{мН}\), як було розраховано раніше.

Сила взаємодії після зближення дорівнюватиме

Як і до зближення, підвішена кулька перебуватиме у стані спокою, а рівнодійна всіх сил, що діють на неї, дорівнюватиме нулю: $$ \overrightarrow{F}=\overrightarrow{T_3}+m\overrightarrow{g}+\overrightarrow{F_{\text{Кл2}}}=0. $$

Цей векторний вираз можна спроєктувати на вертикальну вісь: $$ T_3-mg-F_{\text{Кл2}}=0. $$

Тож можна розрахувати силу натягу підвісу. Оскільки \(T_1=mg,\ F_{\text{Кл2}}=4F_{\text{Кл1}}\), то

Відповідь: 1. 0,5. 2. 3.

ТЕМА: Оптика. Закони заломлення світла.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на закони заломлення світла, зокрема з використанням явища повного внутрішнього відбивання.

Дано:
\(n=1,5\)
\(c=3\cdot 10^8\ \text{м/с}\)

1. Знайти:
\(v\ (\text{тис. км/с})\ -\ ?\)

Абсолютний показник заломлення \(n\) – це відношення швидкості c світла у вакуумі до швидкості \(v\) світла в середовищі: $$ n=\frac cv. $$

Тоді можна розрахувати швидкість поширення світла у склі:

2. Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\delta}\ -\ ?\)

Вираз закону заломлення світла на межі двох середовищ: $$ n_1\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=n_2\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta} $$ де \(n_1\) і \(n_2\) – коефіцієнти заломлення середовищ, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут падіння променю на межу середовищ, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – кут заломлення променю.

Промінь, що падає на призму, заломлюється двічі – на кожній поверхні призми.

Усі кути в законі заломлення відраховуються від перпендикуляр до поверхні. Оскільки падний промінь перпендикулярний до лівої поверхні призми, то кут між перпендикуляром і кутом падіння дорівнює \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}'=0^\circ\).

Оскільки \begin{gather*} n_{\text{пов}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}'=n_{\text{скла}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta},\\[7pt] \text{а}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}'=0^\circ,\ \text{то}\\[7pt] n_{\text{скла}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=0\rightarrow \style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=0^\circ. \end{gather*}

Тож заломлений промінь також перпендикулярний до поверхні призми. На другій поверхні призми кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) – кут падіння променю. Його можна визначити з геометричних міркувань (рис. 1).

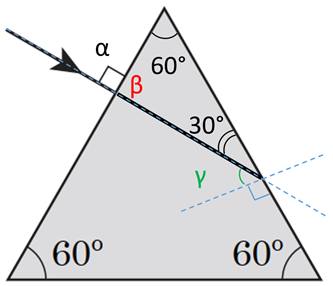
Рис. 1. Визначення кута \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\)

Зважаючи на те, що кути при основі призми дорівнюють \(60^\circ\), третій кут призми дорівнює \(180^\circ -60^\circ -60^\circ =60^\circ\). Трикутник, який промінь відсікає в призмі, прямокутний, один із його гострих кутів – це кут призми, що дорівнює \(60^\circ\). Тобто останній кут цього трикутника дорівнює \(30^\circ\).

Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) відраховують від перпендикуляра, що на рисунку 1 зображений синім пунктиром. Тому

$$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=90^\circ - 30^\circ = 60^\circ. $$

Перед тим, як застосовувати закон заломлення світла вдруге, потрібно перевірити, чи не відбувається в цьому разі повне внутрішнє відбивання. Повне внутрішнє відбивання – це явище відбивання світла на межі двох середовищ. Воно відбувається для всіх кутів, більших за критичний кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_0\), який визначають із умови $$ n\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_0=1. $$

У цьому разі $$ \sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_0=\frac{1}{n_{\text{скла}}}=\frac{1}{1,5}=\frac 23. $$

Це значення синуса не є табличним, тому визначити кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_0\) точно без спеціальних таблиць неможливо. Але для кутів, менших за \(90^\circ\) (а у випадку заломлення світлових промені йдеться саме про такі кути) синус кута збільшується разом зі значенням кута, тобто: $$ \sin x\gt \sin y\rightarrow x\gt y. $$

Із таблиці можна дізнатися, що $$ \sin 60^\circ=\frac{\sqrt{3}}{2}. $$

Для порівняння \(\sqrt{3}/2\) і \(2/3\) їх потрібно звести до спільного знаменника: \begin{gather*} \frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{6};\\[6pt] \frac 23=\frac 46. \end{gather*}

Тепер залишається порівняти чисельники цих дробів.\(\sqrt{3}\) – ірраціональне число, тому його значення треба оцінити.

Якщо \(3\sqrt{3}\gt 4\), то \(\sqrt{3}\gt 4/3\), тобто \(\sqrt{3}\gt 1,(3)\). Для того, щоби перевірити це, потрібно вибрати число, що однозначно більше за \(1,(3)\), наприклад, \(1,5\). \begin{gather*} \sqrt{2,25}=1,5;\\[7pt] 1,5\gt 1,(3)\rightarrow \sqrt{2,25}\gt 1,(3). \end{gather*}

Відомо, що \(\sqrt{2,25}\lt\sqrt{3}\), тому $$ \sqrt{3}\gt\frac 43\rightarrow\frac{\sqrt{3}}{2}\gt\frac 23\rightarrow 60^\circ\gt \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_0. $$

Оскільки кут падіння променю на другу поверхню призми більший, ніж кут повного внутрішнього відбивання, то заломлення не відбудеться, і промінь відбиватиметься від другої поверхні призми (рис. 2).

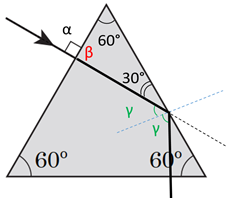
Рис. 2. Повне внутрішнє відбивання променю світла

Кут падіння завжди дорівнює куту відбивання і в цьому разі становить \(60^\circ\). Тепер треба визначити кут, під яким відбитий промінь потрапляє на нижню поверхню призми. Для цього потрібно розглянути трикутник, який відбитий промінь відсікає у призмі (рис. 3). Кут, який відбитий промінь утворює з боковою поверхнею призми, дорівнює \(90^\circ – 60^\circ = 30^\circ\). Кут при основі призми відомий за умовою задачі – \(60^\circ\).

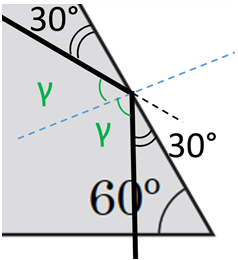
Рис. 3. Визначення кута падіння на нижню поверхню призми

Тоді кут, під яким відбитий промінь падає на нижню поверхню, дорівнює: \(180^\circ –30^\circ – 60^\circ = 90^\circ\). Промінь, що падає на поверхню розділу під прямим кутом, не заломлюється (як це було доведено на початку розв’язку), тому промінь вийде, не змінюючи свого напрямку.

Тому кут відхилення від початкового ходу \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\delta}\) можна визначити з геометричних міркувань (рис. 4).

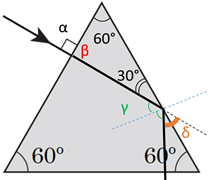
Рис. 4. Визначення відхилення променю від початкового напрямку

На рисунку кут падіння на другу поверхню призми, рівний до нього кут відбивання від цієї поверхні й шуканий кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\delta}\) утворюють розгорнутий кут, тому $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\delta}=180^\circ -2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=180^\circ -2\cdot 60^\circ=60^\circ. $$

Відповідь: 1. 200. 2. 60.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.

Дано:
\(m_1=2\ \text{кг}\)
\(m_2=3\ \text{кг}\)
\(m_3=5\ \text{кг}\)
\(T_{max}=10\ \text{Н}\)

Знайти:
\(F_{max}\ (\text{Н})\ -\ ?\)

У такій конструкції всі три бруски рухатимуться як єдине ціле з однаковим прискоренням і масою \(M\).

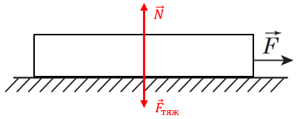
Рис. 1. Схематичне зображення дії сил на бруски як ціле

Для них можна записати 2 закон Ньютона:

Уздовж вертикальної осі бруски не рухаються, тому рівнодійна в цьому напрямку дорівнює 0. Спроєктувавши сили на цей напрямок, можна отримати вираз \begin{gather*} 0+N-F_{\text{тяж}}=0;\\[7pt] N=F_{\text{тяж}}. \end{gather*}

Спроєктувавши другий закон Ньютона на горизонтальний напрямок, можна дійти висновку, що $$ F_{max}+0+0=Ma_{max}. $$

Тож $$ F_{max}=(m_1+m_2+m_3)a_{max}. $$

Обмеження на максимальну силу, а отже й максимальне прискорення, створене міцністю ниток, якими зв’язано бруски.

Цю систему потрібно розглянути як два бруски масою \(m_3\) й \(m_1+m_2\) відповідно (рис. 2).

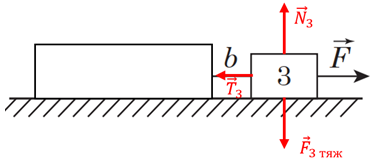
Рис. 2. Схематичне зображення сил, що діють на брусок 3

На брусок 3 діють усі зазначені вище сили й сила натягу нитки. Рухається цей брусок із тим самим прискоренням, яке використано в попередніх розрахунках. Тому можна записати рівнодійну сил, що діють на цей брусок:

Уздовж вертикальної осі брусок 3 не рухається, тому можна зробити той самий висновок, що й у попередніх розрахунках: $$ N_3=F_{3\ \text{тяж}}. $$

Проєкція другого закону Ньютона на горизонтальну вісь матиме вигляд: $$ F_{max}+0+0-T_{3\ \text{max}}=m_3a_{max}. $$

Зважаючи на те, що $$ F_{max}=(m_1+m_2+m_3)a_{max}, $$ можна зробити висновок:

Значення максимальної сили натягу відоме з умови \((10\ \text{Н})\), тому можна виразити максимальне прискорення і знайти максимальну силу:

Відповідь: 20

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння використовувати рівняння стану ідеального газу в розрахункових задачах.

Дано:
\(V=5,5\ \text{л}\)
\(p_1=100\ \text{кПа}\)
\(V_{\text{н}}=0,1\ \text{л}\)
\(N=11\)
\(T=const\)

Знайти:
\(p_2\ (\text{кПа})\ -\ ?\)

Якщо вважати повітря ідеальним газом, то тиск, температуру й об’єм повітря пов’язує рівняння стану ідеального газу \begin{gather*} pV=nRT=\frac mM RT, \end{gather*} де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

Об’єм м’яча і його температура залишаються незмінними, але змінюються тиск і маса газу всередині: \begin{gather*} p_1V=\frac mM RT;\\[6pt] p_2V=\frac{m+\triangle m}{M}RT. \end{gather*}

Тоді можна визначити відношення кінцевого й початкового тисків: $$ \frac{p_2}{p_1}=\frac{m+\triangle m}{m}=1+\frac{\triangle m}{m}. $$

Масу й об’єм пов’язує густина \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) речовини: $$ m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V. $$

За 11 циклів накачування всередину потрапило \(NV_{\text{н}}\) літрів повітря, тому: $$ \triangle m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}NV_{\text{н}}. $$

Тоді

Відповідь: 120

ТЕМА: Маса. Густина. Умова плавання тіл.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на використання умови плавання тіл.

Дано:
\(d=40\ \text{мм}\)
\(h=30\ \text{мм}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{води}}=1000\ \frac{\text{кг}}{\text{м}^3}\)

Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{дерева}}\ \left(\frac{\text{кг}}{\text{м}^3}\right)\ -\ ?\)

За умовою плавання тіл тіло перебуватиме в рівновазі, якщо $$ F_{\text{тяж}}=F_{\text{Арх}}, $$ де \(F_{\text{тяж}}\) – сила тяжіння, \(F_{\text{Арх}}\) – сила Архімеда.

Силу тяжіння визначають за формулою $$ F_{\text{тяж}}=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Масу й густину тіла пов’язує формула $$ m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{т}}V, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{т}}\) – густина тіла, \(V\) – об’єм тіла.

Тому силу тяжіння можна записати як $$ F_{\text{тяж}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{т}}Vg, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{т}}\) – густина тіла, \(V\) – його об’єм, \(g\) – прискорення вільного падіння.

Силу Архімеду визначають за формулою $$ F_{\text{Арх}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{р}}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{р}}\) – густина рідини, \(g\) – прискорення вільного падіння, \(V\) – об’єм тіла, що занурено у воду.

Об’єм дошки можна визначити з її геометричних розмірів: $$ V=dS, $$ де \(d\) – товщина дошки, \(S\) – площа поверхні дошки.

Дошка не повністю занурена під воду, а під час розрахунку сили Архімеда треба використовувати об’єм зануреної під воду частини. Цей об’єм можна розрахувати за формулою $$ V'=hS, $$ де \(h\) – висота дошки під водою, \(S\) – площа поверхні дошки.

Тоді умова плавання дошки матиме вигляд:

Відповідь: 750.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на обчислення коефіцієнта корисної дії теплової машини.

Дано:
\(A = 40\ \text{МДж}\)
\(Q_{\text{х}}=A\)

Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД теплового двигуна визначається за формулою $$ \text{ККД}=\frac{A}{Q_{\text{н}}}\cdot 100\ \text{%}, $$ де \(A\) – корисна робота, виконана двигуном, \(Q_{\text{н}}\) – теплота, отримана від нагрівача.

Частина отриманої теплоти \(Q_{\text{н}}\) використовується на виконання роботи, а решта передається холодильнику. У цій задачі холодильником є середовище. Тоді можна обчислити отриману теплоту:

Після цього можна розрахувати ККД такого двигуна:

Відповідь: 50.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням сили поверхневого натягу.

Дано:
\(r=5\ \text{см}\)
\(m=1,2\ \text{г}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}=70\ \text{мН/м}\)

Знайти:
\(F\ (\text{мН})\ -\ ?\)

На кільце на поверхні води діють сили поверхневого натягу, що утримують його на поверхні, і сила тяжіння. Силу тяжіння можна визначити за формулою $$ F_{\text{тяж}}=mg. $$

Окрім того, кільце обмежує на поверхні дві ділянки – усередині й зовні. Тому з обох боків на нього діятимуть сили поверхневого натягу.

Дріт, із якого зроблене кільце, – тонкий, тому можна вважати, що внутрішній радіус дорівнює зовнішньому радіусу кільця. Тож довжина кільця з боку зовнішньої і внутрішньої поверхні буде однаковою: $$ l=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r_{\text{зовн}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r_{\text{вн}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r. $$

Тоді сила, що необхідна для того, щоби підняти кільце з поверхні, має подолати силу тяжіння і сили поверхневого натягу із зовнішнього і внутрішнього боку:

Відповідь: 56.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку розуміння принципів паралельного і послідовного з’єднання конденсаторів.

Дано:
\(C_1=5\ \text{мкФ}\)
\(C_2=10\ \text{мкФ}\)
\(C_3=20\ \text{мкФ}\)

Знайти:
\(C\ (\text{мкФ})\ -\ ?\)

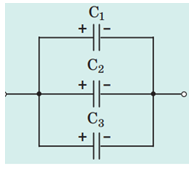
Рис. 1. Схема паралельного підключення конденсаторів

Ємність батареї конденсаторів, з’єднаних паралельно, визначають за формулою:

Відповідь: 35.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.

Завдання скеровано на оцінку вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.

Дано:
\(v_{\mathrm{Be}}=v_p=v\)

Знайти:
\(\frac{r_{\mathrm{Be}}}{r_p}\ -\ ?\)

У рівняннях ядерних реакцій поруч із символом елемента лівим верхнім індексом позначають кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів), а лівим підрядковим – кількість протонів. Тож у цього нукліда Берилію 9 нуклонів, 4 з яких – протони. Маса нейтрона приблизно дорівнює масі протона, тому маса нукліда Берилію у 9 разів більша, ніж маса протона: $$ m_{\mathrm{Be}}=9m_p. $$

Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центру.

Доцентрове прискорення можна знайти з виразу $$ a_{\text{доц}}=\frac{v^2}{R}, $$ де \(v\) – швидкість частинка, а \(R\) – радіус кола, уздовж якого відбувається рух.

За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца: $$ \overrightarrow{F_{\text{Лоренца}}}=Bvq\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(B\) – магнітна індукція поля, \(q\) – заряд частинки, \(v\) – швидкість частинки, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут між вектором магнітної індукції і напрямком руху частинки.

Зважаючи на те, що частинки рухаються в полі по колу, то \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=90^\circ\), а \(\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=1\) (рис. 1).

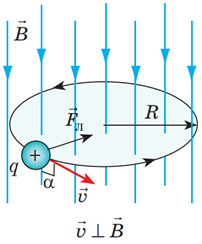
Рис. 1. Схема руху позитивно зарядженої частинки по колу

Тоді можна записати, що $$ \overrightarrow{F_{\text{Лоренца}}}=m\overrightarrow{a_{\text{доц}}}. $$

Оскільки в нукліда Берилію є чотири позитивно заряджені протони й п’ять нейтральних нейтронів, його заряд у чотири рази більший, ніж заряд протона: $$ q_{\mathrm{Be}}=4q_p. $$

Записи другого закону Ньютона для обох частинок такі: \begin{gather*} \left\{ \begin{array}{l} Bv_pq_p=m_p=\frac{v^2_p}{r_p};\\ Bv_{\mathrm{Be}}q_{\mathrm{Be}}=m_{\mathrm{Be}}\frac{v_{\mathrm{Be}}^2}{r_{\mathrm{Be}}}. \end{array} \right. \end{gather*}

Після цього потрібно виразити радіуси кола, уздовж якого здійснюється рух, для обох частинок: $$ \left\{ \begin{array}{l} r_p=m_p\frac{v^2_p}{Bv_pq_p};\\ r_{\mathrm{Be}}=m_{\mathrm{Be}}\frac{v_{\mathrm{Be}}^2}{Bv_{\mathrm{Be}}q_{\mathrm{Be}}}. \end{array} \right. $$

Далі треба підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й α-частинці:

Тобто $$ \frac{r_{\mathrm{Be}}}{r_p}=2,25. $$

Відповідь: 2,25.

ТЕМА: Електромагнітні коливання і хвилі. Власна частота й період електромагнітних коливань. Формула Томсона. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).

Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі на використання формули Томсона й зв’язок між періодом і частотою електромагнітних коливань.

Дано:
\(C_1=26\ \text{нФ}\)
\(L_1=16\ \text{мГн}\)
\(C_2=24\ \text{нФ}\)
\(v_1=v_2\)

Знайти:
\(L_2\ (\text{мГн})\ -\ ?\)

Період коливань \(T\) пов’язаний із їхньою частотою ν формулою $$ T=\frac 1v. $$

Тож, якщо частоти двох коливальних контурів однакові, то однакові і їхні періоди коливань.

Період електромагнітних коливань в електричному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.

Оскільки періоди коливань для двох контурів однакові, \begin{gather*} 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L_1C_1}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L_2C_2};\\[7pt] L_1C_1=L_2C_2. \end{gather*}

Тоді можна визначити індуктивність котушки у другому контурі:

Відповідь: 24.

ТЕМА: Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів. Радіолокація.

Завдання скеровано на перевірку розуміння принципів радіолокації й уміння розв’язувати відповідні розрахункові задачі.

Дано:
\(t=800\ \text{с}\)
\(v=3\cdot 10^8\ \text{м/с}\)

Знайти:
\(s\ -\ ?\)

Радіолокатори посилають короткі імпульси в напрямку, у якому проводять дослідження. Радіохвилі відбиваються від об’єктів, які трапляються на їхньому шляху, і повертаються до локатора. Локатор фіксує час, за який хвиля повернулася, а отже подолала дві відстані до об’єкта (від локатора до об’єкта й від об’єкта знову до локатора).

Тому відстань до об’єкта можна розрахувати за формулою

де \(v\) – швидкість поширення електромагнітних хвиль у середовищі, у якому проводили дослідження.

Відповідь: 120.

ТЕМА: Квантова фізика. Атом і атомне ядро. Радіоактивність.

Завдання скеровано на перевірку розуміння процесу радіоактивного розпаду.

Дано:
\(T_{1/2}=1\ \text{год}\)
\(E'=5\ \text{МеВ}\)
\(t=3\ \text{год}\)
\(N_0=8\cdot 10^{10}\)

Знайти:
\(E\ (\text{мДж})\ -\ ?\)

Енергію, яка виділилася під час розпадів за три години, можна обчислити як добуток кількості розпадів, що відбулися за цей час, й енергії \(N'\), що виділяється під час кожного з них \(E'\): $$ E=E'N'. $$

Період піврозпаду \((Т_{1/2})\) – це фізична величина, що характеризує радіонуклід і дорівнює часу, протягом якого розпадається половина наявної кількості ядер цього радіонукліда.

Тоді можна визначити кількість ядер, що залишилася після розпаду: $$ N=N_02^{\frac{t}{T_{1/2}}}, $$ де \(N\) – кількість ядер, що залишилася після розпаду, \(N_0\) – початкова кількість ядер, \(t\) – час розпаду.

Кількість ядер, що розпалися, дорівнює:

Тоді енергія, що виділилася під час розпаду, дорівнює:

Для того, щоби подати енергію в мДж, потрібно взяти до уваги, що \(1\ \text{еВ}\) – це енергія, необхідна для того, щоби перенести елементарний електричний заряд між точками, різниця потенціалів між якими дорівнює \(1\ \text{В}\). $$ 1\ \text{еВ}=1,6\cdot 10^{-19}\ \text{Кл}\cdot 1\ \text{В}=1,6\cdot 10^{-19}\ \text{дЖ}. $$

Тобто

Відповідь: 56.