ЗНО онлайн 2021 року з фізики – основна сесія

ТЕМА: Властивості газів, рідин і твердих тіл. Види деформації.

Завдання скеровано на перевірку розуміння механізмів деформації різних видів.

Деформація вигину – це деформація, під час якої опукла частина тіла зазнає деформації розтягнення (відстань між шарами молекул збільшується); увігнута частина – деформації стиснення (відстань між шарами молекул зменшується).

Такої деформації зазнає колода, коли по ній проходять люди.

Троси мосту під його вагою зазнають деформації розтягу, ніжка під вагою тумбочки зазнає деформації стиску, а шуруп під час кріплення може зазнати деформації кручення.

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Вага.

Завдання скеровано на перевірку вміння розраховувати вагу тіл, що рухаються з прискоренням.

Вага \((\overrightarrow{P})\) – це сила, яка характеризує дію тіл на опору чи підвіс як наслідок гравітаційного притягання.

Коли тіло рухається лише під дією сили тяжіння, як наприклад камінь, що вільно падає, то воно перебуває в стані невагомості, а отже його вага дорівнює нулю.

Якщо тіло перебуває в стані рівноваги, то його вага за модулем дорівнює силі тяжіння, що діє на нього. Якщо ж тіло рухається з прискоренням, то його вага відрізняється від значення сили тяжіння.

Якщо прискорення напрямлене вертикально вниз, то вагу можна обчислити за формулою $$ P=m(g-a). $$

Униз прискорення напрямлене, коли людина починає рухатися з ліфтовою кабіною вниз. Також униз буде напрямлене доцентрове прискорення, коли автомобіль перебуває в найопуклішій частині опуклого мосту.

Якщо прискорення напрямлене вертикально вгору, то вагу можна обчислити за формулою $$ P=m(g+a). $$

Тож вага космонавта, що перебуває в ракеті під час її старту із Землі, більша за силу тяжіння, що діє на нього.

Відповідь: Б.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її змінення. Способи теплопередачі.

Завдання скеровано на перевірку розуміння механізмів конвекції.

Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу.

Речовини у твердому стані не мають потоків, тому конвекція в них неможлива.

Відповідь: A.

ТЕМА: Основи електростатики. Закон Кулона.

Завдання скеровано на оцінювання розуміння взаємодії між електричними зарядами.

Тіла з однойменними електричними зарядами відштовхуються, а з різнойменними – притягаються. За таким законом змінили своє положення лише кульки на рисунку Б.

Відповідь: Б.

ТЕМА: Оптика. Електромагнітні хвилі. Кванти світла.

Завдання скероване на перевірку розуміння зв’язку між характеристиками квантів світла та електромагнітних хвиль.

Енергію фотона можна обчислити за формулою: $$ E=hv, $$ де \(E\) – енергія фотона, \(v\) – частота випромінювання, \(h\approx 6,62\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\) – стала Планка.

Тож, що більша частота випромінювання, то вища його енергія.

Частота видимого випромінювання збільшується від червоного \((\approx 480\ \text{ТГц})\) до фіолетового \((\approx 790\ \text{ТГц})\), тож й енергія збільшуватиметься так само.

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку розуміння поняття лінійної швидкості обертання і вміння визначати характеристики складного руху.

Велосипед складено з різних частин, чий рух принципово відрізняється: рами, яка під час прямолінійного руху всього велосипеда також рухається поступально, і коліс та педалей, які, крім поступального руху разом з усім велосипедом, здійснюють обертальний.

Позначмо швидкість прямолінійного руху велосипеда як \(v\). Тоді кожна його частина, що рухається поступально, матиме таку саму швидкість. Тому швидкість у точці \(A\) також дорівнюватиме \(v\).

Якщо колесо рухається без проковзування, то лінійна швидкість під час руху по колу будь-якої його точки на зовнішній поверхні має дорівнювати швидкості поступального руху його центра. Тому для точок, зображених на рис. 1 \(V_O = V_K\).

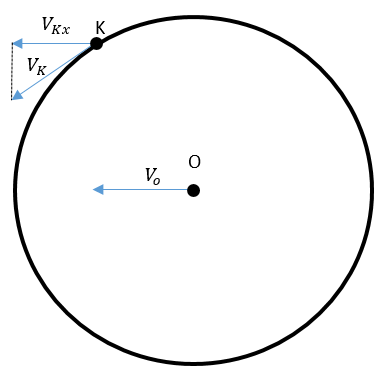
Рис. 1. Лінійна швидкість \(V_O\) обертального руху точки на колі та швидкість \(V_K\) поступального руху центра кола (коло обертається проти годинникової стрілки)

Тоді швидкість руху для будь-якої точки на поверхні кола можна визначити як суму швидкості поступального руху його центра й проєкції на вісь х його лінійної швидкості руху по колу: $$ V=V_{K_x}+V_O $$

Така рівність дійсна для всіх точок зовнішньої поверхні колеса. Тож проекції лінійної швидкості обертального руху за модулем найбільші в найнижчій (Г) і найвищій (Б) точці колеса. У найвищій точці лінійна швидкість обертального руху співнапрямлена зі швидкістю поступального руху всього колеса, а в найнижчій точці – напрямлена протилежно до неї.

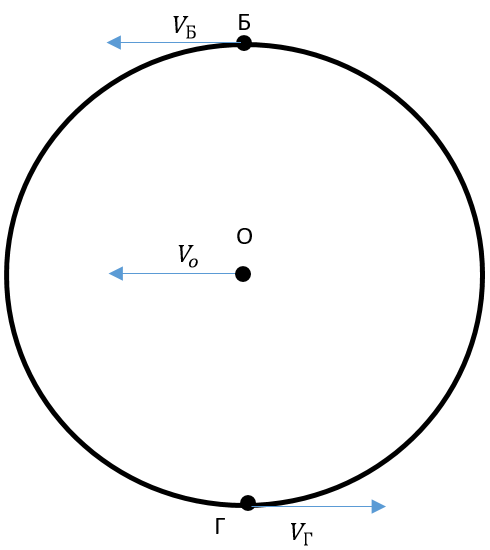
Рис. 2. Напрямок лінійної швидкості обертального руху для точок Б й Г

Тоді загальна швидкість у точці Г дорівнює нулю: $$ V_O-V_{Г}=V_O-V_O=0. $$

А в точці Б: $$ V_O-V_{Б}=V_O+V_O=2V_O. $$ Одна найвища точка колеса матиме найбільшу швидкість, будь-яка інша його точка матиме меншу швидкість.

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.

Завдання скеровано на перевірку вміння обчислювати потенціальну енергію тіла, що перебуває під дією сили тяжіння.

Потенціальна енергія тіла, яке рухається під дією сили тяжіння, можна визначити за формулою $$ E_{пот}=mgh, $$ де \(m\) – маса тіла, \(g=9,8\ \text{м/с}^2\) – прискорення вільного падіння, \(h\) – висота підйому.

Прискорення вільного падіння вважаємо постійним на Землі, маса кульки під час її руху не змінюється, тому найвищу потенціальну енергію кулька матиме в найвищій точці своєї траєкторії – точці Б.

Відповідь: Б.

ТЕМА: Елементи механіки рідин і газів. Гідростатичний тиск.

Завдання скеровано на розуміння понять тиску й сили тиску та вміння визначати гідростатичний тиск.

Якщо всю воду з ширшої посудини перелили у вужчу, то об’єм води не змінився, площа дна посудини зменшилася, а рівень води збільшився, як показано на рисунку 1.

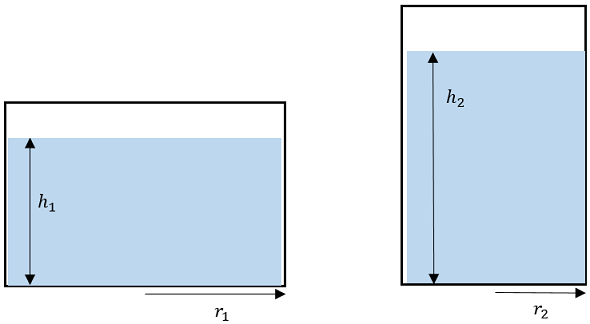
Рис. 1. Рівень води в широкій і високій посудинах

Тиск на дно в обох посудинах є сумою гідростатичного тиску стовпчика води й атмосферного тиску. Гідростатичний тиск \(p\) визначають за формулою $$ p=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gh, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – густина рідини, \(g\) – прискорення вільного падіння, \(h\) – висота стовпчика рідини.

Тиск на дно в першій (широкій) посудині дорівнює: $$ p_1=p_{h_1}+p_{\text{а}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{в}}h_1+p_{\text{а}}. $$ У другій (вузькій) посудині: $$ p_2=p_{h_2}+p_{\text{а}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{в}}h_2+p_{\text{а}}. $$

Вирази для тиску відрізняються лише висотою стовпчика, тож у посудині, де вона більша, тиск на дно також буде більшим.

Сила, що діє на дно обох посудин і створює тиск, – це вага рідини в посудині: $$ P=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Маса води після переливання не змінилася, посудини перебувають у стані спокою, а отже й вага не змінилася. Тож сила тиску під час такого переливання не зміниться.

Відповідь: Б.

ТЕМА: Властивості газів, рідин і твердих тіл. Насичена й ненасичена пара.

Завдання скеровано на перевірку розуміння механізмів переходу від ненасиченої до насиченої пари.

Насичена пара – це пара, яка перебуває в динамічній рівновазі зі своєю рідиною.

Тобто об’єм випаруваної за певний проміжок часу рідини дорівнюватиме об’єму сконденсованої пари. У насиченій парі найвища можлива за певної температури концентрація молекул.

Що вища температура, то вища й концентрація молекул рідини в повітрі, за якої пара є насиченою.

Щоби перетворити водяну пару в повітрі під поршнем на насичену, потрібно або збільшити концентрацію молекул води в повітрі, або знизити температуру.

Концентрацію визначають за формулою $$ n=\frac NV, $$ де \(N\) – кількість молекул у певному об’ємі \(V\).

Якщо не додавати нової води в повітря, концентрацію можна збільшити лише якщо зменшити об’єм посудини.

А під час ізотермічного розширення температура повітря залишається сталою, а його об’єм збільшується, отже концентрація молекул води в повітрі зменшується – пара не може стати насиченою

Б під час ізохорного охолодження об’єм повітря залишається незмінним, а температура знижується. У такому разі концентрація молекул у повітрі не змінюється, але концентрація молекул, що відповідає насиченій парі – зменшується, отже за достатнього охолодження пара може стати насиченою

В під час ізобарного нагрівання і об’єм повітря, і температура збільшуються, отже концентрація молекул зменшується і збільшується концентрація, необхідна для того, щоби пара стала насиченою. За таких умов пара не може стати насиченою

Г під час ізохорного нагрівання об’єм повітря, а отже й концентрація молекул залишається сталою, а температура знижується. У такому разі концентрація молекул, що відповідає насиченій парі, збільшується, тож пара насиченою стати не може

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на перевірку розуміння принципу роботи ідеальної теплової машини й знання графіків ізопроцесів.

Ідеальна теплова машина працює за циклом Карно (рис. 1). Його складниками є ізотермічне розширення (1–2), адіабатне розширення, супроводжуване охолодженням (2–3), ізотермічне зменшення об’єму (3–4) й адіабатне зменшення об’єму, супроводжуване нагріванням (4–1).

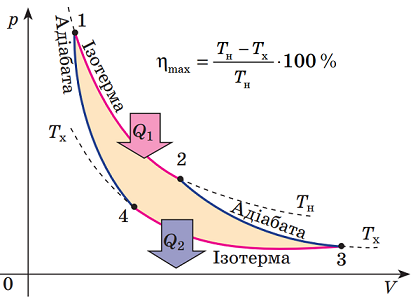
Рис. 1. Цикл Карно

Відповідь: B.

ТЕМА: Властивості газів, рідин і твердих тіл. Види деформацій.

Завдання скеровано на перевірку розуміння поняття пружної деформації.

Пружна деформація – це деформація, що повністю зникає після припинення дії зовнішніх сил.

Відповідь: A.

ТЕМА: Атом й атомне ядро. Основи електростатики. Електричний заряд.

Завдання скеровано на перевірку розуміння будови атома й уміння обчислювати електричний заряд тіл.

Атом – це нейтральна частинка, складниками якої є позитивно заряджене ядро й негативно заряджені електрони. Тому заряд увсіх електронів в атомі дорівнює заряду його ядра.

Ядро містить позитивно заряджені протони й електронейтральні нейтрони. Заряд усіх електронів в атомі дорівнює заряду всіх його протонів. Заряд електрона й заряд протона рівні за модулем, але протилежні за знаком, тому кількість електронів в атомі дорівнює кількості його протонів.

У ядерній фізиці використовують опис ядер, у якому поруч із символом хімічного елемента лівим надрядковим індексом позначають кількість нуклонів у ядрі \(n\) (сумарна кількість протонів і нейтронів), а в лівим підрядковим – кількість протонів \(p\).

В атомі \(^1_1\mathrm{H}\) міститься один протон і, відповідно, один електрон, а в атомі \(^{16}_8\mathrm{O}\) – вісім протонів і вісім електронів.

У молекулі води два атоми Гідрогену, у кожного з яких по одному електрону, й один атом Оксигену, у якому вісім електронів. Разом у молекулі води десять електронів, їхній сумарний заряд

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля – Ленца.

Завдання скеровано на перевірку вміння використовувати закон Джоуля – Ленца.

Кількість теплоти, що виділяється під час проходження струму провідником, визначають за законом Джоуля – Ленца: $$ Q=I^2Rt, $$ де \(I\) – сила струму в провіднику, \(R\) – опір провідника, \(t\) – час проходження струму.

Якщо до збільшення сила струму в провіднику дорівнювала \(I\), то після збільшення вона дорівнюватиме \(I'=4I\).

Тоді:

Тож кількість теплоти збільшиться в 16 разів.

Відповідь: Г.

ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.

Завдання скеровано на перевірку розуміння поняття електромагнітної хвилі.

Для поширення електромагнітних хвиль не потрібне пружне середовище. В іншому разі випромінювання від Сонця не могло би поширюватися крізь космос і досягати Землі.

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.

Завдання скеровано на перевірку розуміння впливу магнітного поля на провідники зі струмом, уміння використовувати правило правої руки й знань про магнітне поле Землі.

Гальванічний елемент із провідником, що з’єднує його краї, утворюють виток зі струмом. Уважаємо, що струм у провіднику рухається від плюса до мінуса, тобто в цьому разі – проти годинникової стрілки. На цей виток діє сила Ампера. Напрямок сили Ампера залежить від кута між напрямком ліній магнітної індукції та напрямком протікання струму.

У витку в різних його частинах напрямок протікання струму різний. У крайній лівій його частині струм напрямлений вертикально вниз, а в крайній правій точці – вертикально вгору (рис. 1).

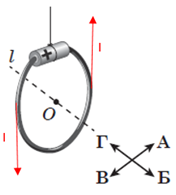
Рис. 1. Напрямок протікання струму в крайніх лівій і правій точках витка зі струмом

Тоді в цих точках сила Ампера матиме протилежний напрямок. Це створює обертальний момент, який можна обчислити за формулою $$ M=BIS\sin \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(B\) – магнітна індукція, \(I\) – сила струму, \(S\) – площа рамки, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут між напрямком протікання струму й напрямком ліній магнітної індукції.

Рамка зупинилася, коли обертальний момент сил Ампера, що на неї діють, зменшився до нуля. Це можливо, якщо \(\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=0\), а отже напрямок протікання струму став перпендикулярним до ліній магнітної індукції в усіх точках контуру. Це можливо лише за умови, що лінії магнітної індукції пронизують контур уздовж напрямку Г – Б на рисунку 1.

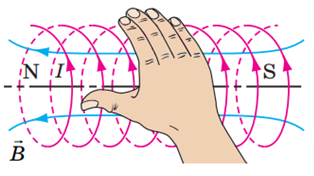
Рис. 2. Правило правої руки

Якщо чотири пальці правої руки обгорнути за напрямком струму в контурі, то великий палець укаже на напрямок Б, тобто північний полюс витка попереду (рис. 3).

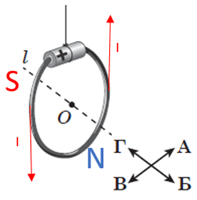
Рис. 3. Застосування правила правої руки

Географічний напрямок північ – це напрямок, на який указує північний полюс магнітної стрілки компаса, тобто з погляду фізики він є південним магнітним полюсом. Тому напрямок Б вказує на географічний напрямок північ.

Відповідь: Б.

ТЕМА: Оптика. Закони заломлення світла.

Завдання скеровано на оцінювання розуміння законів заломлення світла.

За законом заломлення променів $$ n_1\sin(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha})=n_2\sin(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}), $$ де \(n_1\) і \(n_2\) – це відповідні абсолютні показники заломлення речовин, між якими відбувається перехід, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут падіння променів, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – кут заломлення променів.

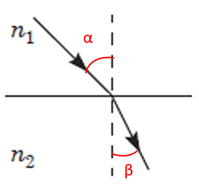
Рис. 1. Закон заломлення променів

Кут падіння і кут заломлення мають бути меншими за 90° (рис. 1).

За графіком функції \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) (рис. 2) можна визначити, що на проміжку від 0° до 90° \(\left(\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}\right)\) функція монотонно зростає, тобто зі збільшенням кута збільшується і значення його синуса.

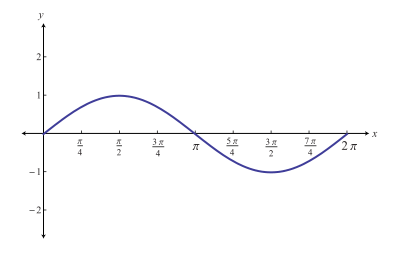
Рис. 2. Графік функції \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\)

Отже, якщо кут заломлення менший, ніж кут падіння, то і синус кута заломлення буде меншим за синус кута падіння. Тож, щоб закон заломлення виконувався, якщо кут падіння більший за кут відбивання, то показник заломлення в середовищі падаючого променю має бути меншим за показник заломлення і середовищі заломленого променю.

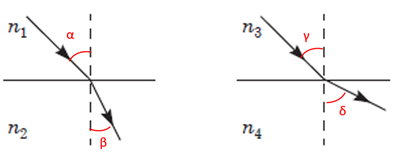
Рис. 3. Умова завдання

За умовою завдання для у першому випадку кут заломлення \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) менший за кут падіння \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\), тож $$ n_1\lt n_2. $$

У другому випадку кут падіння \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) менший за кут заломлення \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\delta}\), тож: $$ n_3\gt n_4. $$

Відповідь: Б.

ТЕМА: Оптика. Інтерференція світла та її практичне застосування.

Завдання скеровано на перевірку розуміння механізмів інтерференції та її проявів у природі.

На тонкій поверхні мильної бульбашки відбувається інтерференція (рис. 1).

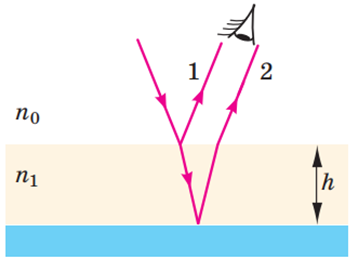
Рис. 1. Механізм інтерференції

Одна частина променю, що падає на зовнішню поверхню мильної плівки, відбивається від неї, а інша проходить у товщу плівки й заломлюється. Ця частина променю відбивається вже на другій поверхні плівки й заломлюється на шляху назад із плівки в повітря. Дві частини променю є когерентними, але вони пройшли різну відстань, тож мають певну різницю ходу. У результаті хвилі накладаються одна на одну, у певних місцях підсилюючи одна одну, а в інших ослаблюючи – утворюється інтерференційна картина.

Сонячне світло складається з багатьох хвиль різної довжини, тому інтерференційна картина для кожного кольору буде інша. Для підсилення якогось конкретного кольору товщину плівки треба дібрати так, щоби хвилі мали різницю ходу, кратну парній кількості півхвиль. Якщо товщина плівки різниться в різних місцях, як це часто буває в мильних бульбашках, то в різних її частинах підсилюватиметься хвиля іншого кольору й утворюватиметься кольоровий візерунок.

Відповідь: B.

ТЕМА: Атом й атомне ядро.

Завдання скеровано на оцінювання розуміння дослідів Резерфорда та їхнього значення для розуміння будови атома.

α-частинки – позитивно заряджені важкі частинки (ядра атомів Гелію). Під час їхнього наближення до позитивно зарядженого важкого ядра Ауруму починають діяти електростатичні сили відштовхування α-частинок від ядра (рис. 1).

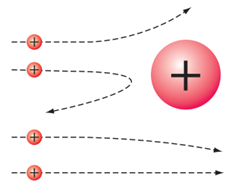
Рис. 1. Траєкторії α-частинок, що пролітають поряд із ядром

Відповідь: Б.

ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.

Завдання скеровано на оцінювання вміння аналізувати рівняння ядерних реакцій і розуміння процесу ядерного розпаду.

Під час радіоактивних розпадів масове число дорівнює кількості нуклонів у ядрі, а зарядове число – кількості протонів.

За альфа розпаду масове число нукліда зменшується на чотири, а зарядове – на два за схемою $$ ^n_pX=^{n-4}_{p-2}Z+^{4}_2\mathrm{He}. $$

Під час бета-розпаду зарядове число нукліда збільшується на одиницю за схемою $$ ^n_pX=^n_{p+1}X+^{\ \ \ 0}_{-1}e. $$

Послідовні розрахунки для трьох альфа-розпадів такі:

Послідовні розрахунки для двох бета-розпадів:

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Закон всесвітнього тяжіння.

Завдання скеровано на перевірку розуміння законів Ньютона й закону всесвітнього тяжіння і їхнього застосування для описування реальних ситуацій.

Закони, про які йдеться в цьому завданні:

• перший закон Ньютона – існують такі системи відліку, відносно яких тіло зберігає стан спокою або рівномірного прямолінійного руху, якщо на нього не діють жодні сили або якщо ці сили скомпенсовані;
• другий закон Ньютона – прискорення, якого набуває тіло внаслідок дії сили, прямо пропорційне цій силі й обернено пропорційне масі тіла: $$ \overrightarrow{a}=\frac{\overrightarrow{F}}{m}; $$
• третій закон Ньютона – тіла взаємодіють із силами, що мають одну природу, напрямлені вздовж однієї прямої, рівні за модулем і протилежні за напрямком: $$ \overrightarrow{F_1}=-\overrightarrow{F_2}; $$
• закон всесвітнього тяжіння – будь-які два тіла притягуються одне до одного із силою, яка прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними: $$ F=G\frac{m_1m_2}{r^2}. $$

А зменшення маси автомобіля, що привело до його прискорення, є прикладом другого закону Ньютона

Б нагрівання гальмівних колодок під час гальмування пов’язане зі зміною їхньої внутрішньої енергії внаслідок роботи сил тертя, отже цей приклад не пов’язаний із наведеними законами

В кинутий угору камінь притягається до Землі за законом всесвітнього тяжіння

Г якщо сила тертя компенсує силу тяжіння, то всі сили, що діють на дощову краплю під час її падіння, скомпенсовані. Тому те, що вона рухається рівномірно й прямолінійно – це приклад для першого закону Ньютона

Д сила удару, який комар завдав лобовому склу, і сила удару, яке скло завдало комарові, рівні за третім законом Ньютона

Відповідь: 1Г, 2А, 3Д, 4В.

ТЕМА: Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку розуміння практичного застосування деяких фізичних законів і властивостей речовин.

1 щоб убезпечити поверхні від шкідливого впливу вологи, їх укривають шаром лаку. Після висихання лак створює плівку, погано змочувану водою. Тож вода відштовхується від такої поверхні й не може зруйнувати її

2 різні матеріали по-різному розширюються під час нагрівання, тобто мають різні коефіцієнти теплового розширення. Це використовують у біметалевих регуляторах – приладах різної конструкції, що працюють завдяки біметалевій пластині з двох шарів різних металів, тісно з’єднаних між собою. Оскільки коефіцієнти теплового розширення в цих металів різні, то під час нагрівання пластина не просто розширюється, а вигинається. Такий вигин використовують для розірвання електричного кола й припинення нагрівання. Коли ж температура знову знижується, вигин пластини зменшується, контакт відновлюється і нагрівання триває. Це дає змогу підтримувати температуру системи в певному діапазоні

3 основною відмінністю дизельного двигуна від карбюраторного є те, що запалювальна суміш загоряється без зовнішньої іскри. Займання відбувається внаслідок сильного нагрівання під час адіабатного стиснення

4 конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу. Застосуванням цього фізичного явища є обігрівання приміщень радіаторами. Вони передають тепло до найближчих шарів повітря. Густина теплих шарів повітря зменшується і вони починають підніматися вгору, витісняючи холодніші шари повітря вниз, де вже вони починають нагріватися. Під час підйому теплі шари повітря також передають тепло холоднішим, тому, поки досягають верху приміщення, стають суттєво холоднішими за шари повітря тільки-но нагріті радіаторами. Тож конвекція триває.

Відповідь: 1В, 2А, 3Г, 4Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах.

Завдання скеровано на оцінювання розуміння механізмів різних видів газових розрядів й умов їхнього застосування в техніці.

Дуговий газовий розряд виникає за високої температури (понад 4000 °С) і майже за будь-якого тиску. Це яскраве дугоподібне полум’я. За такої високої температури з поверхні катода безперервно «випаровуються» електрони, а в стовпі розпеченого газу відбувається термічна йонізація. Це забезпечує ідеальні умови для впливу на металеві поверхні без прямого контакту приладу з ними.

Іскровий газовий розряд виникає за атмосферного тиску й великої напруги між електродами. Його тривалість дуже мала, тому його часто використовують під час підпалювання робочої суміші в циліндрі двигуна внутрішнього згоряння. Цикл усередині циліндра загалом займає мало часу й потребує швидкого нагріву для роботи.

Жеврійний (тліючий) газовий розряд виникає за невеликої напруги між електродами й низького тиску. Цей тип розряду приводить до жевріння в трубках із низьким тиском газу навіть під дією слабкого електричного поля, що робить його найзручнішим для використання в освітленні.

Коронний газовий розряд виникає за близького до атмосферного тиску в сильному \((E\gt 500\ \text{кВ/м})\), різко неоднорідному електричному полі. Сильне поле змушує йони рухатися з великою швидкістю, а отже й кінетичною енергією, що зумовлює ударну іонізацію. Численні йони газу під час проходження між електронами заряджають дрібні частинки пилу, що також рухаються в полі й осідають на одному з електродів, звідки їх легко прибрати.

Відповідь: 1В, 2Д, 3А, 4Г.

ТЕМА: Сила тяжіння. Сила пружності. Сила кулона. Ядерні сили.

Завдання скеровано на перевірку розуміння впливу сил різної природи на природні явища.

1 електронейтральні нейтрони й позитивно заряджені протони утримуються в ядрах (й альфа-частинках, що є ядрами атомів Гелію, зокрема) завдяки дії ядерних сил

2 куля деформує броню в момент зіткнення. Залежно від величини цієї деформації броня повертається в попередній стан (зазнає пружної деформації), зберігає деформацію після зіткнення (зазнає пластичної деформації) або руйнується. Подальший рух кулі також від цього залежить, адже завдяки силі пружності, що виникає в броні, куля може зрикошетити й змінити напрямок руху чи його швидкість

3 причиною руху Місяця навколо Землі є її сила тяжіння

4 часто рух негативно зарядженого електрона в атомі зумовлений його кулонівською взаємодією з позитивно зарядженим ядром.

Відповідь: 1Г, 2Д, 3А, 4Б.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку вміння використовувати закон збереження імпульсу й уміння визначати швидкість у різних системах відліку.

Дано:
\(m_2=45\ \text{т}\)
\(m_1=55\ \text{т}\)
\(v_1=3\ \text{м/с}\)
\(v=3,9\ \text{м/с}\)
\(t=26\ \text{с}\)

1. Знайти:
\(v_2\ \left(\frac{\text{м}}{\text{с}}\right)\ -\ ?\)

За законом збереження імпульсу сума імпульсів тіл до зіткнення дорівнюватиме сумі імпульсів тіл після.

Імпульс розраховують за формулою $$ \overrightarrow{p}=m\overrightarrow{v}, $$ де \(m\) – маса тіла, а \(\overrightarrow{v}\) – його швидкість.

До зіткнення вагони рухаються незалежно й мають власні імпульси, а після зіткнення вони рухаються як одне тіло з єдиним імпульсом, спільною швидкістю і масою, яка дорівнює сумі мас двох вагонів. Тобто

2. Знайти:
\(l_0\ (\text{м})\ -\ ?\)

Для того, щоби визначити відстань, яку вагони пройшли до зіткнення, потрібно визначити їхню швидкість один відносно одного. Вагони рухаються в одному напрямку, тому їхня швидкість один відносно одного буде меншою, ніж відносно землі. Швидкість другого вагона відносно першого можна обчислити за формулою $$ v_{2(1)}=v_2-v_1=5\ \frac{\text{м}}{\text{с}}-3\ \frac{\text{м}}{\text{с}}=2\ \frac{\text{м}}{\text{с}}. $$

Початкова відстань, яку другий вагон скоротив до \(0\) за \(26\ \text{с}\), дорівнює $$ l_0= v_{2(1)}t=2\ \frac{\text{м}}{\text{с}}\cdot 26\ \text{с}=52\ \text{м}. $$

Відповідь: 1. 5. 2. 52.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння застосовувати рівняння стану ідеального газу.

1. Дано:
\(V=0,83\ \text{м}^3\)
\(T_1=250\ \text{К}\)
\(p_1=100\ \text{кПа}\)
\(T_2=300\ \text{К}\)
\(p_2=195\ \text{кПа}\)
\(M=32\ \frac{\text{г}}{\text{моль}}\)
\(R=8,3\ \frac{\text{Дж}}{\text{моль}\cdot\text{К}}\)

1. Знайти:
\(n_1\ (\text{моль})\ -\ ?\)

Температура \(T\), тиск \(p\) й об’єм \(V\) пов’язані рівнянням стану ідеального газу $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(n\) – кількість речовини.

Для початкового стану можна записати рівняння $$ p_1V=n_1RT_1. $$

Тобто

2. Знайти:
\(\triangle m\ (\text{кг})\ -\ ?\)

Кількість речовини пов’язана з її масою формулою $$ n=\frac mM, $$ де \(m\) – маса речовини, \(M\) – її молярна маса.

Після обчислення різниці в кількості речовини у двох станах можна обчислити й різницю мас газу. Аналогічно до \(n_1\) можна обчислити \(n_2\):

Тоді

Відповідь: 1. 40. 2. 0,8.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі за допомогою закону Ома для повного кола, а також вміння інтерпретувати схеми електричного кола.

1. Дано:
\(r=1\ \text{Ом}\)

1. Знайти:
\(R_{\text{рис. 2}}\ -\ ?\)

Реостат – це елемент кола зі змінним опором. Зазвичай реостат – це довгий провідник, повзунок якого дає змогу включити в коло його частину будь-якої довжини. Чим менша частина реостата включена в коло, тим менший його опір. Опір провідника можна визначити за його геометричними параметрами: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – питомий опір, \(l\) – довжина, \(S\) – площа перерізу провідника.

Фізичну будову реостата відображено в його символі для схематичного зображення електричного кола. Стрілка в позначенні показує, яку саме частину реостата включено в коло.

У цій задачі максимальний опір реостата відповідає крайньому правому положенню. За рисунком a можна визначити, що довжина провідника становить 6 клітинок. Масштаб рисунка невідомий, тому вважатимемо, що довжина реостата становить 6 умовних одиниць довжини (у. о. д.). На рисунку a в коло включена ділянка реостата, довжина якої становить 5 умовних одиниць. Ні питомий опір провідника, ні його поперечний переріз при цьому не відрізняються від цих його параметрів за максимального опору. Лише довжина ділянки вдвічі менша, тож можна обчислити опір реостата в положенні, зображеному на рисунку a:

2. Знайти:
\(\frac{P_{\text{рис. б}}}{P_{\text{рис. a}}}\ -\ ?\)

Потужність струму в реостаті можна обчислити за формулою $$ P=UI, $$ де \(U\) – напруга, \(I\) – сила струму.

За законом Ома напруга, сила струму й опір ділянки кола пов’язані між собою: $$ I=\frac UR. $$

З огляду на те, що жодних відомостей про напругу в умові завдання немає, можна виразити її із закону Ома й підставити у формулу для потужності: $$ P=I^2R. $$

Аналогічно можна розрахувати опір реостата для положення, зображеного на рисунку 1:

За законом Ома для повного кола можна визначити силу струму: $$ I=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R+r}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\) – електрорушійна сила джерела, \(r\) – внутрішній опір джерела, \(R\) – опір зовнішньої ділянки кола.

Тоді для рисунків 1 і 2 можна записати такі вирази відповідно:

Відповідь: 1. 5. 2. 1,8.

ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на перевірку вміння за графіком аналізувати коливання за допомогою формули Томсона.

Дано:
\(L=50\ \text{мГн}\)

1. Знайти:
\(T\ (\text{мс})\ -\ ?\)

Період коливань сили струму в контурі можна визначити за графіком. За один період система повертається в те саме положення, у якому вона перебувала. У разі залежності сили струму й від часу \(t\) система повертається у початкове положення (\(i = 0\) і продовжує спадання) за \(4\ \text{мс}\). Тому \(T=4\ \text{мс}\).

2. Знайти:
\(C\ (\text{мкФ})\ -\ ?\)

Період коливання коливального контуру пов’язаний з електроємністю конденсатора й індуктивністю котушки формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.

З неї можемо визначити вираз для електроємності:

Відповідь: 1. 4. 2. 8.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага. Рівномірний рух по колу.

Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.

Дано:
\(m=40\ \text{кг}\)
\(P=800\ \text{Н}\)
\(l=2,5\ \text{м}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

Знайти:
\(v\ (\text{м/с})\ -\ ?\)

Гойдалка рухається за траєкторією, що є частиною кола. Тож вона матиме доцентрове прискорення, напрямлене в бік кріплення підвісу гойдалки. У найнижчій точці це прискорення буде напрямлене вертикально вгору. Вага тіл, що рухаються із прискоренням, що напрямлене вертикально вгору, може бути розрахована за формулою: $$ P=m(a+g). $$

Доцентрове прискорення можна обчислити з виразу $$ a_{\text{доц}}=\frac{v^2}{R}=\frac{v^2}{l}, $$ де \(v\) – швидкість гойдалки, а \(R\) – радіус обертання, що дорівнює довжині підвісу гойдалки.

Тоді

Відповідь: 5

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Сила тяжіння. Рівномірний рух по колу. Кінетична енергія.

Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.

Дано:
\(F_{\text{тяж}}=4\ \text{кН}\)
\(R=10000\ \text{км}\)

Знайти:
\(E_{\text{кін}}\ (\text{ГДж})\ -\ ?\)

Кінетичну енергію тіла можна обчислити за формулою \begin{gather*} E_k=\frac{mv^2}{2}, \end{gather*} де \(m\) – маса тіла, а \(v\) – швидкість його руху.

Під час руху супутника навколо Землі його швидкість спрямована по дотичній до кола, а прискорення – до центру.

Доцентрове прискорення можна обчислити з виразу $$ a_{\text{доц}}=\frac{v^2}{R}, $$ де \(v\) – швидкість супутника, а \(R\) – радіус обертання.

За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії: $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на частинки в площині напрямку руху є сила тяжіння Землі: $$ \overrightarrow{F_{\text{тяж}}}=m\overrightarrow{g}. $$

Тобто $$ mg=m\frac{v^2}{R}. $$

Із цього рівняння можна виразити добуток маси й квадрату швидкості та підставити його у формулу для кінетичної енергії:

Відповідь: 20

ТЕМА: Робота. Сила Архімеда.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про силу Архімеда.

Дано:
\(H=4\ \text{м}\)
\(m=600\ \text{кг}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{бетону}}=2000\ \frac{\text{кг}}{\text{м}^3}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{води}}=1000\ \frac{\text{кг}}{\text{м}^3}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

Знайти:
\(A_{min}\ (\text{кДж})\ -\ ?\)

Для того, щоби перевернути блок, достатньо його центр мас підняти на висоту, на якій він у вертикальному положенні. Оскільки блок циліндричний, то в обох положеннях він на половині висоти блока (рис. 1).

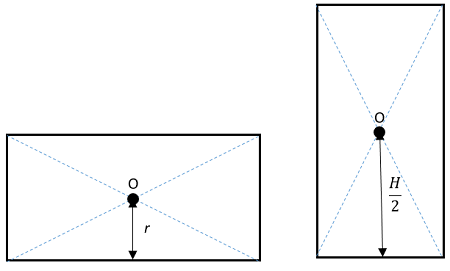
Рис. 1. Положення центра мас у вертикальному й горизонтальному положенні

Оскільки поперечні розміри стовпа за умовою враховувати не потрібно, то можна вважати, що під час перевертання центр мас піднімають на половину всієї висоти \(H\).

Рівнодійну сил, що діють на блок, можна обчислити за формулою $$ \overrightarrow{F}=\overrightarrow{F_{\text{тяж}}}+\overrightarrow{F_{\text{Арх}}}. $$

Сила тяжіння діє вертикально вниз, притягуючи блок до землі, а сила Архімеда виштовхує блок вертикально вгору, інші сили на блок не діють. Якщо вважати напрямок «вертикально вниз» додатним, \begin{gather*} F_x=0;\\[6pt] F_y=mg-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{води}}gV_{\text{блока}}. \end{gather*}

Маса тіла пов’язана з його густиною формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV, $$ де \(m\) – маса тіла, \(V\) – його об’єм.

Тоді

Оскільки об’єму блока невідомий, із дужок можна винести його густину:

Тоді робота, необхідна для підняття центра мас бетонного блока на половину його висоти, дорівнює

Відповідь: 6.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку вміння застосовувати закон Бойля – Маріотта.

Дано:
\(T_1=T_2\)
\(V_1=8\ \text{л}\)
\(V_2=6\ \text{л}\)
\(p_2=p_1+4\ \text{кПа}\)

Знайти:
\(p_1\ (\text{кПа})\ -\ ?\)

Для того, щоби правильно аналізувати зміни всіх фізичних величин, потрібно використати рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. $$

Згідно нього добуток тиску на об’єм, поділений на температуру, залишається сталим під час переходу зі стану 1 у стан 2.

Для ізотермічного процесу рівняння Клапейрона спрощують і перетворюють на рівняння, яким описують закон Бойля – Маріотта: $$ p_1V_1=p_2V_2. $$

Якщо \(p_1=x\), рівняння набуває вигляду $$ x\ \text{кПа}\cdot 8\ \text{л}=(x+4)\ \text{кПа}\cdot 6\ \text{л}. $$

Після переведення всіх одиниць в одиниці системи СІ:

Відповідно \(p_1=12\ \text{кПа}\).

Відповідь: 12.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про відносну вологість і точку роси.

Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=80\ \text{%}\)
\(t=25\ ^\circ\text{С}\)

Знайти:
\(t_{\text{туман}}\ -\ ?\)

Туман почне формуватися, коли температура повітря сягне точки роси. Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.

Для визначення температури, що є точкою роси, потрібно визначити густину водяної пари в повітрі за початкових умов і за таблицею визначити температуру, за якої ця густина є густиною насиченої пари.

Пригадаймо, що густина водяної пари в повітрі та відносна вологість пов’язані формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}}\cdot 100\ \text{%}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) – відносна вологість повітря, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}\) – густина насиченої пари, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}\) – густина водяної пари в повітрі.

Тож можна визначити густину водяної пари в повітрі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}}{100\ \text{%}} $$

Густина насиченої пари за температури \(25\ ^\circ\text{С}\) за таблицею становить \(23,0\ \text{г/см}^3\), тоді:

Найближча величина густини насиченої пари до її обчисленої густини – \(18,3\ \text{г/см}^3\), що відповідає \(21\ ^\circ\text{С}\). $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}=21\ \frac{\text{г}}{\text{см}^3} $$

Відповідь: 21.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку знання законів послідовного й паралельного з’єднання конденсаторів.

Енергію конденсатора можна обчислити за формулою $$ W_{\text{конденсатора}}=\frac{q^2}{2C}, $$ де \(q\) – це максимальний заряд на обкладинці конденсатора, а \(C\) – його ємність.

Електроємність конденсатора визначають за формулою $$ C=\frac qU, $$ де \(U\) – напруга між обкладинками, \(q\) – максимальний заряд на обкладинці.

У схемі, наведеній у завданні, конденсатор 1 послідовно підключений до конденсаторів 2 й 3, що підключені один до одного паралельно.

Напруга на паралельно підключених елементах однакова: $$ U_{2+3}=U_2=U_3. $$

За умовою ємність усіх конденсаторів рівна, тож \begin{gather*} q_2=C_2U_2=CU_{2+3};\\[7pt] q_3=C_3U_3=CU_{2+3};\\[7pt] q_2=q_3. \end{gather*}

Якщо конденсатори підключені паралельно, то максимальний заряд на їхніх котушках $$ q_{2+3}=q_2+q_3=2q_2. $$

Ємність таких конденсаторів можна обчислити за формулою $$ C_{2+3}=C_2+C_3=2C. $$

Якщо конденсатори підключено послідовно, то максимальні заряди на їхніх обкладинках рівні: $$ q_{1+2+3}=q_1=q_{2+3} $$

Тож $$ q_1=2q_2. $$

Тоді можна обчислити енергії конденсаторів: \begin{gather*} W_2=\frac{q^2_2}{2C_2}=\frac{q^2_2}{2C};\\[6pt] W_1=\frac{q^2_1}{2C_1}=\frac{(2q_2)^2}{2C}=\frac{4q^2_2}{2C}=4W_2. \end{gather*}

Відповідь: 4.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, у яких ідеться про залежність опору провідника від його геометричних параметрів.

Дано:
\(R_1=1\ \text{Ом}\)
\(d_1=2d_2\)

Знайти:
\(R_2\ -\ ?\)

Опір провідника залежить від його геометричних характеристик: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – питомий опір речовини, із якої виготовлений провідник; \(l\) – довжина провідника; \(S\) – площа його поперечного перерізу.

Якщо вважати форму перерізу провідника колом, його площу можна обчислити за формулою $$ S=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r^2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac d2\right)^2=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d}{4}. $$

Під час шліфування ні довжина, ні питомий опір провідника не змінювались, тобто

Відповідь: 4.

ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.

Завдання скеровано на перевірку розуміння основних фізичних величин, пов’язаних із механічними коливаннями.

Амплітуда коливань – це максимальне відхилення від положення рівноваги.

Якщо коливання гармонічні, і на рисунку 1 зображено крайнє ліве положення, на рисунку 2 – крайнє праве, то посередині між ними положення рівноваги. Амплітуда – це і є відстань від положення рівноваги до будь-якого крайнього положення. Тож відстань між двома крайніми положеннями відповідає двом амплітудам.

На рисунку 1 лівий край візка стоїть на відмітці \(10\ \text{см}\), а на рисунку 2 той самий край стоїть на відмітці \(40\ \text{см}\), тому подвійна амплітуда дорівнюватиме \begin{gather*} 2A=40\ \text{см}-10\ \text{см}=30\ \text{см};\\[6pt] A=\frac{30\ \text{см}}{2}=15\ \text{см}. \end{gather*}

Відповідь: 15.

ТЕМА: Оптика. Лінза. Формула тонкої лінзи.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосування законів геометричної оптики й формули тонкої лінзи.

Дано:
\(F=20\ \text{см}\)
\(l=12\ \text{мм}\)
\(L=6\ \text{м}\)

Знайти:
\(D\ -\ ?\)

Фокусну відстань лінзи та її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи: $$ \frac 1F=\frac 1d+\frac 1f, $$ де \(d\) – відстань від об’єкта до лінзи, а \(f\) – відстань від лінзи до зображення, \(F\) – фокусна відстань лінзи.

Розміри зображення і предмета з їхніми відстанями від лінзи пов’язує лінійне збільшення лінзи Г: $$ \boldsymbol Г=\frac lL=\frac fd. $$

З виразу для лінійного збільшення лінзи можемо обчислити відстань \(f\) від предмета до лінзи: $$ f=\frac{ld}{L}. $$ Тоді

Відповідь: 100.

ТЕМА: Квантова фізика. Світлові кванти. Рівняння теплового балансу.

Завдання скеровано на перевірку вміння розв’язувати комплексні задачі із застосуванням рівняння теплового балансу, зокрема із джерелом теплоти, що пов’язане з квантами світла.

Дано:
\(m=0,5\ \text{г}\)
\(N=2,1\cdot 10^{18}\ \frac{1}{\text{с}}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=600\ \text{нм}\)
\(t=1\ \text{хв}\)
\(c_{\text{води}}=4200\ \frac{Дж}{\text{кг}\ \cdot\ \text{К}}\)
\(c=3,8\cdot 10^{8}\ \frac{\text{м}}{\text{с}}\)
\(h=6,63\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\)

Знайти:
\(\Delta T\ (\text{К})\ -\ ?\)

Кількість отриманої теплоти й зміна температури пов’язані формулою $$ Q=cm\Delta T, $$ де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – її маса, \(\Delta t\) – зміна температури під час охолодження.

Теплоту крапля отримує від поглинання енергії фотонів, яку для одного фотона визначають за формулою $$ E=h\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}, $$ де \(E\) – енергія фотона, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) – частота випромінювання, \(h\) – стала Планка.

Частота й довжина хвилі пов’язані виразом $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}. $$

Якщо за одну секунду крапля отримує \(N\) фотонів, то за одну хвилину вона отримає \(tN\) фотонів. Тоді можна розрахувати всю енергію, отриману від них за формулою $$ Q=NtE=Nth\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=Nth\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}. $$ Тоді можна доповнити рівняння теплового балансу: $$ Nth\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}=c_{\text{води}}m\Delta T. $$ І з цього виразу можна обчислити різницю температур \(\Delta T\):

Відповідь: 20.