ЗНО онлайн 2021 року з фізики – додаткова сесія

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на перевірку вміння визначати ціну поділки шкали.

Оскільки шкала динамометра розрахована на \(4\ \text{Н}\), то ціна між великими поділками (відмічені синім на рис. 1) дорівнює \(4\ \text{Н}:4=1\ \text{Н}\).

Між двома великими поділками є \(10\) малих. Тоді ціна одної малої поділки дорівнює \(1\ \text{Н}:10=0,1\ \text{Н}\).

Рис. 1. Визначення ціни поділки

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку вміння визначати доцентрове прискорення на криволінійній траєкторії.

Криволінійна траєкторія утворена елементами двох кіл із різними радіусами (рис. 1).

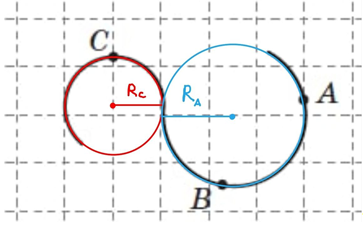
Рис. 1. Радіуси криволінійної траєкторії

Точки А і В лежать на більшому колі, а точка С – на меншому, тож \(R_C\lt R_B=R_A\).

Доцентрове прискорення можна обчислити з виразу: $$ a_\text{доц}=\frac{v^2}{R}, $$ де \(v\) – швидкість руху тіла, а \(R\) – радіус обертання.

Оскільки модуль лінійної швидкості не змінюється, то можна записати прискорення в кожній із точок: \begin{gather*} a_C=\frac{v^2}{R_C};\\[6pt] a_B=\frac{v^2}{R_B}=\frac{v^2}{R_A}=a_A. \end{gather*}

Оскільки \(R_C\lt R_B=R_A\), то \(a_C\gt a_B=a_A\).

Цей вираз можна записати в іншому вигляді: $$ a_A=a_B\lt a_C. $$

Відповідь: B.

ТЕМА: Основи термодинаміки. Тепловий рух.

Завдання скеровано на перевірку розуміння поняття броунівського руху.

Броунівський рух – хаотичний рух видимих у мікроскоп малих макрочастинок, завислих у рідині або газі, який відбувається під дією ударів молекул рідини або газу.

Тобто рух броунівської частинки (як наприклад частинка пилу чи квіткового пилку) залежить від руху молекул рідини чи газу, у яких вони перебувають. Молекули зіштовхуються з броунівською частинкою під час теплового руху і передають їй частину свого імпульсу.

Імпульс визначають за формулою $$ p=mv, $$ де \(m\) – маса тіла, \(v\) – його швидкість.

Тоді швидкість частинки можна визначити за формулою $$ v=\frac pm . $$

Що швидше рухаються молекули, то частіше вони зіштовхуються з броунівською частинкою, і тим більший імпульс вона отримує, а отже більшою буде її швидкість.

Окрім того, що менша маса частинка, то більшою буде її швидкість за однакового переданого імпульсу.

Відповідь: A.

ТЕМА: Електричне коло.

Завдання скеровано на оцінювання знань умовних позначень для створення схем електричних кіл.

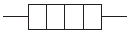	– нагрівальний елемент.
	– резистор.
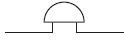	– електричний дзвінок.
	– запобіжник.

Відповідь: Г.

ТЕМА: Квантова фізика. Атом та атомне ядро.

Завдання скероване на перевірку знань про нуклони.

Атомна одиниця маси дорівнює \(1/12\) маси нукліда Карбону \(\mathrm{C‐12}\), у якому \(12\) нуклонів (протонів і нейтронів).

Маса електронів набагато менша за масу нуклонів, тож нею можна знехтувати. Можна вважати, що маса нуклона дорівнює 1 а. о. м. (точніше визначена маса протона трохи відрізняється від маси нейтрона: \(m_p=1,00728\ \text{а. о. м.}\), \(m_n=1,00866\ \text{а. о. м.}\); якщо округлити ці значення до одиниць, то \(m_p=m_n=1\).

Протон – це позитивно заряджена частинка, за модулем її заряд дорівнює елементарному.

Відповідь: B.

ТЕМА: Механіка. Основи динаміки. Вага.

Завдання скеровано на перевірку вміння розраховувати вагу тіл, що рухаються з прискоренням.

Якщо тіло перебуває в стані спокою або рухається рівномірно, то його вага за модулем дорівнює силі тяжіння, що діє на нього.

Якщо ж тіло рухається з прискоренням, то його вага відрізнятиметься від значення сили тяжіння.

Якщо прискорення напрямлене вертикально вниз, то вагу можна обчислити за формулою $$ P=m(g-a). $$

Униз прискорення напрямлене, коли ліфт рухатиметься з 10-го поверху на 1-й і збільшуватиме швидкість.

Якщо прискорення напрямлене вертикально вгору, то вагу можна обчислити за формулою $$ P=m(g+a). $$

Угору прискорення напрямлене, коли ліфт рухається з 1-го поверху на 10-й і збільшує швидкість.

Відповідь: A.

ТЕМА: ТЕМА: Механіка. Умови рівноваги. Прості механізми.

Завдання скеровано на оцінку розуміння принципів роботи простих механізмів, зокрема рухомого й нерухомого блока.

Нерухомий блок (рис. 1, а) не дає виграшу в силі – він дає змогу змінити лише напрямок прикладання сили, тобто: $$ |F_1|=|F_2|. $$

Рухомий блок (рис. 1, б) дає виграш у силі у 2 рази. Тобто необхідна для піднімання вантажів за допомогою рухомого блока сила буде вдвічі менша, ніж якщо вантаж піднімати без використання механізмів: $$ |F_1|=\frac{|F_2|}{2}. $$

Тож виграш у силі в системі залежить лише від кількості рухомих блоків.

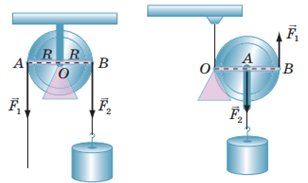
Рис. 1. Нерухомий (а) і рухомий (б) блоки

Нехай сила \(F\) – це сила, необхідна для підняття вантажу без будь-яких механізмів.

Тоді після першого рухомого блока виграш у силі дорівнюватиме 2: $$ |F_1|=\frac{|F|}{2}. $$

Другий рухомий блок знову дасть виграш у силі у 2 рази відносно попереднього блока, тобто виграш у силі – у 4 рази відносно переміщення вантажу без механізмів: $$ |F_2|=\frac{|F_1|}{2}=\frac{|F|}{4}. $$

Третій рухомий блок дає виграш у силі вже у 8 разів відносно переміщення вантажу без механізмів: $$ |F_3|=\frac{|F_2|}{2}=\frac{|F_1|}{4}=\frac{|F|}{8}. $$

Відповідь: B.

Механіка. Елементи динаміки рідин i газів. Умова плавання тіл.

Завдання скеровано на перевірку розуміння поняття густини та вміння застосовувати закон Архімеда.

Силу Архімеда можна визначити за формулою $$ F_\text{Арх}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{рідини}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{рідини}\) − густина рідини, \(g\) – прискорення вільного падіння, \(V\) – об’єм тіла.

Силу тяжіння визначають за формулою $$ F=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Густина речовини \((\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho})\) – це фізична величина, яка характеризує речовину й дорівнює відношенню маси суцільного тіла, виготовленого із цієї речовини, до об’єму цього тіла: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV, $$ де \(m\) – маса тіла, а \(V\) – об’єм тіла.

Тоді масу тіла можна виразити як $$ m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V. $$

Тоді силу тяжіння можна записати як: $$ F_\text{тяж}=mg=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{тіла}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{тіла}\) – густина тіла, \(g\) – прискорення вільного падіння, \(V\) – об’єм тіла.

Вважатимемо, що на тіло в рідині діє лише сила тяжіння, що напрямлена вниз, і виштовхувальна сила Архімеда, напрямлена вгору. За другим законом Ньютона $$ \overrightarrow{F_\text{тяж}}+\overrightarrow{F_\text{Арх}}=m\overrightarrow{a}. $$

Тіло плаває в товщі рідини, а не спливає на поверхню чи тоне, тому прискорення \(a=0\). Відповідно $$ \overrightarrow{F_\text{тяж}}+\overrightarrow{F_\text{Арх}}=0. $$

Якщо спрямувати вісь x у напрямку прискорення вільного падіння, можна спроєктувати векторне рівняння:

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використання рівняння стану ідеального газу.

Об’єм, температура й тиск газу пов’язані між собою рівнянням стану ідеального газу: $$ pV=nRT=\frac mM RT, $$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

З рівняння стану ідеального газу можна виразити тиск \(p\): $$ p=\frac mM \frac{RT}{V}. $$

За графіком (рис. 1) можна визначити тиск та об’єм у точках 1 і 2. На графіку не вказано одиниці вимірювання, тож вважатимемо, що 1 клітинка вздовж осі \(T\) відповідає 1 умовній одиниці температури (у. о. т.), а 1 клітинка вздовж осі \(V\) відповідає 1 умовній одиниці об’єму (у. о. о.).

Тоді для точок 1 і 2 об’єм і температура дорівнюють:

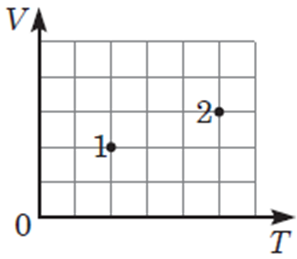
Рис. 1. Графік у координатах \(Vt\)

Можна визначити тиск у точках 1 і 2 в умовних одиницях тиску (у. о. тиску):

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку розуміння зв’язку між макроскопічними й мікроскопічними параметрами ідеального газу.

Концентрацію визначають за формулою $$ n=\frac NV, $$ де \(N\) – кількість молекул у певному об’ємі \(V\).

Тоді, якщо за сталої маси концентрація залишається незмінною, то й об’єм у такому процесі не змінюється.

Середню кінетичну енергію молекул можна визначити за формулою $$ \overline{E_\text{кін}}=\frac{m_0\overline{v^2}}{2}, $$ де \(m_0\) – маса одної молекули, \(\overline{v^2}\) – середній квадрат швидкості молекул.

Що вища температура, то вищий середній квадрат швидкості молекул. Тож, щоб у газі певної маси концентрація молекул залишалася сталою, а їхня середня кінетична енергія зростала, газ потрібно ізохорно нагрівати.

Відповідь: A.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на перевірку розуміння фізичних принципів роботи психрометра.

Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий вологою тканиною. Вода з тканини завжди випаровується і швидкість випаровування залежить від того, яка вологість повітря навколо.

Під час випаровування температура вологого термометра знижується, і це зниження залежить від швидкості випаровування, а отже й від вологості.

Для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.

Якщо температура обох термометрів однакова, то це означає, що випаровування з вологого термометра не відбувається. Це можливо лише за умови, що вологість повітря становить 100 %.

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку розуміння поняття електроємності.

Електроємність – це фізична величина, яка характеризує здатність провідника накопичувати заряд.

Відповідь: Г.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах.

Завдання скеровано на перевірку розуміння механізму іскрового розряду.

Іскровий розряд виникає за атмосферного тиску та великої напруги.

Іскровий розряд має вигляд яскравих зиґзаґів із багатьма розгалуженнями.

Нетривалий, супроводжуваний характерним тріском.

Прикладом іскрового розряду є блискавка.

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.

Завдання скеровано на перевірку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.

За правилом правої руки можна визначити напрямок ліній магнітної індукції навколо провідника зі струмом.

Якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом.

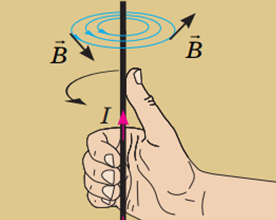
Рис. 1. Правило правої руки

Для провідника, про який ідеться в задачі, можна визначити напрямок ліній індукції магнітного поля (рис. 2).

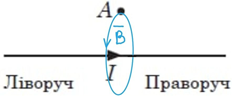
Рис. 2. Лінії індукції магнітного поля

Тож у точці \(A\) напрямок індукції магнітного поля – напрямок на спостерігача (перпендикулярно до сторінки).

Напрямок ліній магнітної індукції – це і є напрямок, в якому зорієнтований північний полюс магнітної стрілки в даній точці.

Відповідь: Б.

ТЕМА: Механічні коливання і хвилі.

Завдання скеровано на перевірку розуміння закономірностей зміни енергії під час коливального руху.

Якщо маятник настінного годинника має частоту коливань 2 Гц, то він виконує 2 коливання за секунду. Тоді за хвилину він робить 120 коливань.

Потенціальну енергію маятника можна визначити за формулою $$ U=mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.

На найбільшій висоті маятник перебуває в крайніх точках своєї траєкторії (рис. 1).

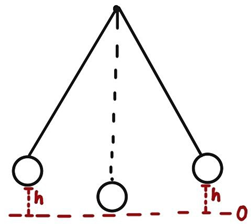
Рис. 1. Крайні положення коливання маятника

Тож за одне коливання маятник двічі опиняється в точках, де його потенціальна енергія максимальна. Тоді за 120 коливань його потенціальна енергія буде максимальною 240 разів.

Відповідь: Г.

ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.

Коливальний контур – це фізичний пристрій, який складається з послідовно з’єднаних конденсатора й котушки індуктивності (рис. 1).

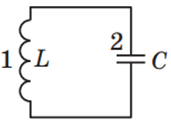
Рис. 1. Електрична схема коливального контуру:
1 – котушка індуктивності, 2 – конденсатор

В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат: $$ W_\text{конденсатора}=\frac{CU^2}{2}, $$ де \(U\) – напруга на обкладинках конденсатора, а \(C\) – його ємність.

За умовою (рис. 2) спостереження розпочато тоді, коли напруга на конденсаторі максимальна. У цей момент енергія конденсатора також буде максимальною.

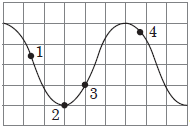
Рис. 2. Показники осцилографа

Під час коливань у контурі енергія повністю зарядженого конденсатора перетікатиме в енергію котушки, яку можна визначити за формулою: $$ W_\text{котушки}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.

У контурі електрони, що накопичилися на одній з обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм у колі. У результаті цього конденсатор почне розряджатися, напруга на його обкладинках зменшується, а отже зменшуватиметься і його енергія.

У котушці ж сила струму поступово збільшуватиметься, а разом із нею збільшуватиметься й енергія магнітного поля, яке вона створює. Коли конденсатор розрядиться повністю, струм у котушці стане максимальним.

Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається, а струм у котушці поступово зменшується.

Унаслідок цього процесу заряд з однієї обкладинки конденсатора опиниться на іншій обкладинці. Тож тепер конденсатор заряджений протилежно до початкового стану, і напруга на ньому за модулем дорівнює початковій напрузі, але має протилежний знак (точка 2 на рисунку 2).

Отже і в початковій точці, і в точці 2 (рис. 2) енергія конденсатора максимальна, а енергія котушки дорівнює нулю. Енергія конденсатора дорівнює нулю тоді (енергія котушки максимальна), коли напруга на конденсаторі дорівнює нулю. На рисунку, наведеному в умові, цей стан відповідає лінії посередині, як це зображено на рисунку 3:

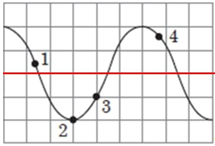
Рис. 3. Нульовий рівень напруги на конденсаторі

Що ближче точка до нульового рівня по вертикалі, то менша напруга на конденсаторі за модулем, і то більша енергія котушки. Тож у точці 1 енергія котушки буде найбільшою з усіх відмічених точок.

Відповідь: A.

ТЕМА: Оптика. Оптика. Світло як електромагнітна хвиля.

Завдання скеровано на перевірку розуміння принципів поширення світла.

Природне світло утворене багатьма хвилями, випроміненими різними атомами. Через це в пучку природного світла є безліч напрямків коливання вектора напруженості електричного поля.

Унаслідок поляризації в пучку світла залишаються тільки хвилі певного напрямку (або напрямків).

Для поляризації використовують спеціальні фільтри – поляроїди (або поляризатори).

Рис. 1. Принцип роботи поляризатора

Поляризатор (рис. 1) працює як щілина, яка пропускає коливання, здійснювані лише в певному напрямку. Якби електромагнітні хвилі були поздовжніми, то поляризатор не вносив би ніяких змін, але зміни інтенсивності зафіксовано експериментально (адже значну частину променів відбиває поляризатор). Тому світло може бути лише поперечною хвилею.

Відповідь: Б.

ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на оцінювання розуміння постулатів спеціальної теорії відносності.

Швидкість світла є однаковою в усіх інерціальних системах відліку незалежно від того, із якою швидкістю рухається джерело. Тож попри те, що ракета з прожектором рухається зі швидкістю \(\frac 45c\), швидкість світла, яку зафіксують на Землі, все одно дорівнюватиме \(c\).

Відповідь: Г.

ТЕМА: Квантова фізика. Атом та атомне ядро. Альфа-, бета- та гамма-випромінювання.

Завдання скеровано на оцінювання розуміння принципів захисту від йонізувального випромінювання.

Для захисту від α-випромінювання досить аркуша паперу, для захисту від β-випромінювання вже потрібен шар алюмінію понад 1 мм завтовшки, для захисту від γ-випромінювання використовують товстий шар бетону чи свинцю, а від потоку нейтронів захищає шар води.

Відповідь: B.

ТЕМА: Енергія. Робота. Потужність. Сила.

Завдання скеровано на перевірку розуміння понять енергії, потужності, сили й прискорення.

Потужність \(P\) – це фізична величина, яка характеризує швидкість виконання роботи.

Енергія \(E\) – це фізична величина, яка характеризує здатність тіла виконати роботу.

Сила \(F\) – це векторна фізична величина, що є мірою взаємодії тіл, у результаті якої тіло набуває прискорення або деформується.

Прискорення \(a\) – це векторна фізична величина, яка характеризує зміну швидкості руху тіла.

Відповідь: 1В, 2Д, 3Б, 4А.

ТЕМА: Молекулярна фізика і термодинаміка. Квантова фізика.

Завдання скеровано на перевірку розуміння фізичного змісту фізичних сталих.

Розв’язання завдання потребує знання визначень фізичних величин і вміння аналізувати розмірності.

Розмірність сталої Авогадро – \(\frac{1}{\text{моль}}\), що відповідає діленню кількості молекул на кількість речовини.

Стала Авогадро – це число, що відповідає кількості атомів (молекул) у будь-якій речовині кількістю \(1\ \text{моль}\).

Розмірність сталої Больцмана \(\frac{\text{Дж}}{\text{К}}\), що відповідає діленню енергії на температуру.

Сталу Больцмана використовують для встановлення зв’язку між середньою кінетичною енергією руху молекул і температурою ідеального газу: $$ \overline{E_k}=\frac 32 kT. $$

Якщо температура змінюється, то змінюється і середня кінетична енергія молекул: $$ \Delta\overline{E_k}=\frac 32 k\Delta T. $$

Звідси можна виразити сталу Больцмана: $$ k=\frac 23 \frac{\Delta \overline{E_k}}{\Delta T}. $$ Експериментально сталу Больцмана визначають саме за цією формулою.

Розмірність сталої Планка – \(\text{Дж}\cdot \text{с}\), що відповідає енергії, поділеній на частоту.

За гіпотезою Планка молекули випромінюють енергію порційно, і кількість цієї енергії пропорційна до частоти випромінювання: $$ E=hv. $$

Відповідно стала Планка $$ h=\frac Ev. $$

Гравітаційна стала фігурує в законі Всесвітнього тяжіння: $$ F=G\frac{m_1m_2}{r_2}. $$

Якщо маса обох тіл становить 1 кг, відстань між ними – 1 м, то $$ F_0=G\frac{1\ \text{кг}\cdot 1\ \text{кг}}{1\ \text{м}^2}=G\frac{\text{кг}^2}{\text{м}^2}. $$

Тож сила взаємодії таких тіл за модулем дорівнює гравітаційній сталій.

До того ж сила має розмірність \(H\), і єдина величина з невідомою розмірністю – це \(G\), тобто: $$ [G]=\frac{1\ \text{Н}}{\frac{1\ \text{кг}\ \cdot\ 1\ \text{кг}}{1\ \text{м}^2}}=\frac{1\ \text{Н}\cdot 1\ \text{м}^2}{1\ \text{кг}\cdot 1\ \text{кг}}=1\frac{\text{Н}\cdot \text{м}^2}{\text{кг}^2}. $$

Відповідь: 1Б, 2А, 3Г, 4В.

ТЕМА: Перетворення енергії в коливальному контурі. Закон Джоуля – Ленца. Рівняння теплового балансу.

Завдання скеровано на оцінювання знання формул для визначення енергії коливального контуру, кількості теплоти, що виділяється під час згоряння палива, і закону Джоуля – Ленца.

\(\frac{LI^2}{2}\), де \(L\) – індуктивність, \(I\) – сила струму – енергія магнітного поля струму.

\(I^2Rt\) де \(I\) – сила струму, \(R\) – опір, \(t\) – час – кількість теплоти, що виділяється в провіднику під час проходження електричного струму.

\(qm\) де \(q\) – питома теплота згоряння палива, \(m\) – маса – кількість теплоти, що виділяється внаслідок горіння палива.

\(\frac{CU^2}{2}\) де \(U\) – напруга, а \(C\) – електроємність – енергія зарядженого конденсатора.

Відповідь: 1В, 2А, 3Г, 4Д.

ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку вміння пов’язувати поняття з теми «Механічні коливання і хвилі» та їхні приклади в реальному житті.

Вільні гармонічні коливання – це коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги, а координата \(x\) тіла, що коливається, змінюється із часом \(t\) за законом косинуса (або синуса).

Так можна описати рух пружинного маятника.

Вимушені коливання – це коливання, які відбуваються в системі внаслідок дії зовнішньої сили, що періодично змінюється.

Шари повітря поруч із гучномовцем постійно зазнають впливу від мембрани, що їх штовхає, тобто вони коливаються під дією зовнішньої сили.

Затухаючі (згасні) коливання – це коливання, амплітуда яких із часом зменшується.

Прикладом такого руху є рух тонкої гілки дерева, з якої злетів птах.

Автоколивання – незатухаючі (незгасні) коливання, які відбуваються в системі за рахунок надходження енергії від постійного джерела, що регулює сама система. Тобто в самій системі є механізм, який дає їй змогу перерозподіляти енергію під час коливань.

У маятниковому годиннику є храпове колесо (3 на рис. 1), що має зазублини. У процесі коливання маятник (1 на рис. 1) відхиляється і чіпляється то за ту, то за ту зазублину двостороннім кріпленням у верхній його частині (4 на рис. 1). Як наслідок, коли кріплення чіпляється за зазублину, маятник отримує додатковий поштовх.

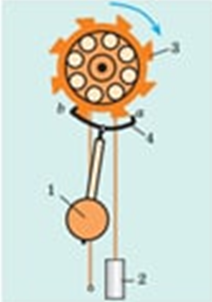
Рис. 1. Схема роботи маятникового годинника

Відповідь: 1Д, 2В, 3Г, 4Б.

ТЕМА: Механіка. Рух під дією сили тяжіння.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про рух тіла під дією сили тяжіння.

Дано:
\(v_0=20\ \text{м/с}\)
\(g=10\ \text{м/с}^2\)

1. Знайти:
\(|v(3\ \text{c})|\ \left(\frac{\text{м}}{\text{с}}\right)\ -\ ?\)

Оберімо вісь для обчислень і намалюймо схему руху тіла.

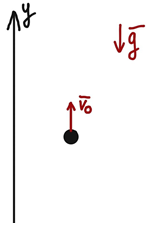
Рис. 1. Схема руху тіла

Рух тіла під дією сили тяжіння можна описати рівняннями для рівноприскореного руху. Замінимо прискорення в цьому рівнянні на прискорення вільного падіння. Тіло кинуте вертикально вгору, а прискорення вільного падіння спрямоване вниз. Тож початкова швидкість на прискорення вільного падіння матимуть різні знаки: $$ v=v_0+at=v_0-gt. $$

Тоді в момент часу 3 швидкість тіла

За умовою задачі потрібно визначити модуль швидкості на третій секунді руху, тож $$ |-10\ \frac{\text{м}}{\text{с}}|=10\ \frac{\text{м}}{\text{с}}. $$

2. Знайти:
\(l\ (\text{м})\ -\ ?\)

Шлях тіла, кинутого вгору, складатиметься з двох частин: підйому й падіння. Вважатимемо, що тіло кинули з рівня землі, оскільки це не суперечить умові задачі. Тоді шлях підйому та шлях падіння будуть рівні.

Обчислімо шлях підйому. Для цього оцінимо його час. У момент, коли тіло перестає підніматися і починає падати, його швидкість дорівнює нулю. Тоді маємо рівняння, з якого можемо визначити час падіння:

Шлях також можемо визначити за формулою для рівноприскореного руху, з урахуванням того, що початкова швидкість і прискорення мають різні значення:

Тоді повний шлях тіла до падіння дорівнюватиме: $$ l=2\cdot l(2)=2\cdot 20\ \text{м}=40\ \text{м}. $$

Відповідь: 1. 10. 2. 40.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на рівняння теплового балансу.

1. Дано:
\(m_\text{води}=200\ \text{г}\)
\(t_\text{води}=24\ ^\circ\text{C}\)
\(m_\text{сталі}=2,1\ \text{кг}\)
\(t_\text{рівноваги}=74\ ^\circ\text{C}\)
\(c_\text{води}=4200\ \frac{\text{Дж}}{\text{кг}\ \cdot\ ^\circ\text{C}}\)
\(c_\text{сталі}=500\ \frac{\text{Дж}}{\text{кг}\ \cdot\ ^\circ\text{C}}\)

1. Знайти:
\(Q\ (\text{кДж})\ -\ ?\)

Необхідну для нагрівання енергію можна визначити за формулою: $$ Q=cm\Delta t, $$ де \(c\) – питома теплоємність речовини, \(m\) – маса речовини, \(\Delta t=(t_2-t_1)\) – різниця температур.

Маса води в одиницях СІ становить: \(200\ \text{г}=0,2\ \text{кг}\).

Тоді енергію, необхідну для нагрівання води від \(24\) до \(74\ ^\circ\text{C}\) можна визначити за формулою:

2. Знайти:
\(t_\text{сталі}\ (^\circ\text{C})\ -\ ?\)

Енергія, необхідна для нагрівання води, не могла взятися нізвідки. У системі немає зовнішнього джерела тепла (нагрівач, пічка, тощо). Єдиним джерелом додаткової енергії могла стати сталева кулька, що мала температуру вищу, за початкову температуру води. Енергія, що виділилась під час ї охолодження якраз і пішла на нагрівання води.

Енергію, що виділилась від час охолодження також можемо визначити за формулою: $$ Q=cm\Delta t, $$ де \(c\) – питома теплоємність речовини, \(m\) – маса речовини, \(\Delta t=(t_2-t_1)\) – різниця температур.

Варто пам’ятати, що енергію, яку тіло втратило, позначають як від’ємну. Тож маємо рівняння:

Відповідь: 1. 42. 2. 114.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі за допомогою закону Ома для повного кола.

За рисунком 1, наведеним в умові завданні, можна визначити покази амперметра в обох положеннях вимикача. Для цього визначимо ціну поділки шкали амперметра.

Рис. 1. Умова завдання

Ціна великої поділки амперметра дорівнює \(1\ –\ 0,5 = 0,5\ (\text{А})\). Між двома великими поділками є \(10\) маленьких, тож ціна маленької поділки дорівнює \(0,5 : 10 = 0,05\ \text{А}\).

Тоді в першому положенні (на рисунку 1 ліворуч) сила струму, виміряна амперметром, дорівнює \(0,5 + 4\cdot 0,05 = 0,5 + 0,2 = 0,7 (\text{А})\). У другому положенні (на рисунку праворуч) сила струму, виміряна амперметром, дорівнює \(0,05\ –\ 0,05 = 0,45\ \text{А}\).

Також з рисунку можна зрозуміти, що перемикач дає змогу вибрати, який із резисторів (А чи Б) підключають у коло.

1. Дано:
\(R_A=1\ \text{Ом}\)
\(r=0,08\ \text{Ом}\)
\(I_\text{А}=0,7\ \text{А}\)
\(I_\text{Б}=0,45\ \text{А}\)

1. Знайти:
\(U_\text{А}(B)\ -\ ?\)

Напругу на обкладинках гальванічного елемента можна визначити із закону Ома для ділянки кола: $$ I=\frac UR, $$ де \(R\) – опір, \(U\) – напруга.

Тоді напруга дорівнює: $$ U=I_\text{А}R_\text{А}=0,7\ \text{А}\cdot 1\ \text{Ом}=0,7\ \text{В}. $$

2. Знайти:
\(R_\text{Б}(\text{Ом})\ -\ ?\)

Напруга на обкладинках під час зміни положення перемикача змінюється, але електрорушійна сила (ЕРС) джерела струму – ні. ЕРС для положення вимикача на резисторі А за законом Ома для повного кола: $$ I=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R+r}, $$ де \(R\) – опір провідників у колі, а \(r\) – внутрішній опір джерела струму.

Тоді ЕРС дорівнює:

Тоді із закону Ома для повного кола можна визначити опір провідника Б:

Відповідь: 1. 0,7. 2. 2.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань. Довжина хвилі.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на зв’язок різних параметрів коливальної системи.

Дано:
\(l=500\ \text{м}\)
\(t=1\ \text{хв}\ 40\ \text{с}\)
\(N=20\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=10\ \text{с}\)

1. Знайти:
\(T\ (\text{с})\ -\ ?\)

Період коливань поверхні води збігається з періодом хвилі. Період хвилі – це час, за який хвиля проходить відстань, що дорівнює одній її довжині. Період хвилі можна обчислити за формулою $$ T=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}}{N}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}\) – час руху хвилі, \(N\) – кількість повних довжин хвиль за час \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}\).

Кількість довжин хвиль можна визначити, порахувавши кількість гребнів хвиль, що вдаряються об берег, тобто сплесків. За умовою \(20\) сплесків на березі було зафіксовано за \(10\ \text{с}\), тому $$ T=\frac{10\ \text{с}}{20}=0,5\ \text{с}. $$

2. Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\ (\text{м})\ -\ ?\)

Відстань між двома сусідніми гребнями хвиль – це довжина хвилі. Вона пов’язана з періодом за формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=Tv, $$ де \(T\) – період хвилі, \(v\) – швидкість хвилі.

Швидкість хвилі можна обчислити за формулою $$ v=\frac lt, $$ де \(l\) – шлях, пройдений гребнем хвилі, \(t\) – час.

Тобто

Відповідь: 1. 0,5. 2. 2,5.

ТЕМА: Механіка. Основи динаміки. Сила. Гравітаційна взаємодія.

Завдання скеровано на перевірку розуміння принципів гравітаційної взаємодії.

Дано:
\(R_Z=2R_\text{Землі}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_Z=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{Землі}}{4}\)
\(F_\text{тяж Землі}=1600\ \text{Н}\)

Знайти:
\(F_{\text{тяж}Z}\ -\ ?\)

Силу тяжіння визначають за формулою $$ F_\text{тяж}=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Прискорення вільного падіння можна пов’язати із законом всесвітнього тяжіння: $$ F=G\frac{m_1m_2}{r^2}, $$ де \(G\) – гравітаційна стала, \(m_1\) – маса першого тіла, \(m_2\) – маса другого тіла, \(r\) – відстань між ними.

Сила тяжіння – це сила, із якою Земля чи інше астрономічне тіло притягують до себе тіла, що перебувають на їхній поверхні, тож вона є частковим випадком сили із закону всесвітнього тяжіння.

Тож можна записати рівність виразів для сили тяжіння і закону всесвітнього тяжіння, у якому одне тіло – це планета, а інше – корабель. Вважатимемо, що відстань між центрами мас корабля і планети дорівнює її радіусу: $$ G=\frac{m_\text{корабля}M}{R^2}=m_\text{корабля}g. $$

Тож, якщо поділити обидва вирази на масу корабля, дістаємо: $$ G\frac{M}{R^2}=g. $$

На планетах із різними радіусами й масами прискорення вільного падіння буде різним.

Прискорення вільного падіння на Землі: $$ g_\text{Землі}=G\frac{M_\text{Землі}}{R^2_\text{Землі}}. $$

На планеті Z: $$ g_Z=G\frac{M_Z}{R^2_Z}. $$

За умовою маси планет невідомі, але відомі їхні середні густини. Середню густину планети можна визначити за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac MV, $$ де \(M\) – маса планети, \(V\) – об’єм планети.

Форма планет близька до сферичної внаслідок дії гравітації, тож їхній об’єм можна визначити як об’єм сфери: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac{M}{\frac 43 \style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^3}. $$

Тоді масу планети можна виразити через її середню густину: $$ M=\frac 43\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}R^3. $$

Тоді силу тяжіння на Землі можна виразити як

А на планеті Z сила тяжіння

Відповідь: 800.

ТЕМА: Механіка. Основи динаміки. Момент сил.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на визначення моменту сил.

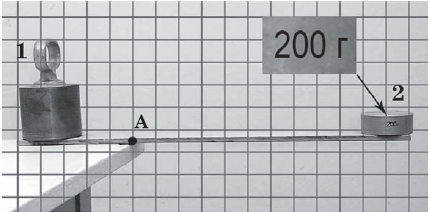
Рис. 1. Умова завдання

На рисунку 1 зображено важіль із точкою опори в точці A. Ліве плече важеля (із вантажем 1) лежить на столі, а праве плече (із вантажем 2) звисає. Важіль перебуває в рівновазі. За розміткою на рисунку можна визначити довжину правого й лівого плеча як відстань від точки прикладення сили тяжіння (центру мас тіла) до точки опори.

Довжина лівого плеча – \(4,5\) клітинки, а оскільки період сітки дорівнює \(5\ \text{см}\), то довжина цього плеча в сантиметрах дорівнює \(4,5\cdot 5 = 22,5\ \text{см}\).

Довжина лівого плеча – \(11\) клітинок, тобто \(11\cdot 5 = 55\ \text{см}\).

Дано:
\(d_1=22,5\ \text{см}\)
\(d_2=55\ \text{см}\)
\(m_2=200\ \text{г}\)

Знайти:
\(M_2\ -\ ?\)

Горизонтальна вісь, що проходить через точку A перпендикулярно до рейки – це вісь обертання важеля.

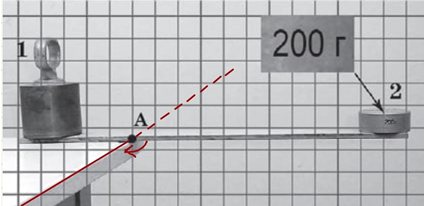
Рис. 2. Вісь обертання важеля

Момент сили відносно цієї осі дорівнюватиме:

Відповідь: 1,1.

ТЕМА: Рівняння теплового балансу. Потенціальна енергія.

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі на рівняння теплового балансу й потенціальну енергію тіла.

Дано:
\(t_1=20\ ^\circ\text{С}\)
\(t_2=18\ ^\circ\text{С}\)
\(\Delta =1\ \text{%}\)
\(c=380\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

Знайти:
\(h\ (\text{м})\ -\ ?\)

Утрачену під час охолодження кульки енергію можна розрахувати за формулою $$ Q=cm\Delta t, $$ де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – її маса, \(\Delta t\) – зміна температури під час охолодження.

Енергію тіло втрачає, тому отримане число – від’ємне, тож знак «мінус» тут позначає лише напрямок руху енергії. У подальших розрахунках використовуватимемо значення \(Q=760m\ \text{Дж}\).

Коли тіло піднімається на певну висоту, то збільшується його потенціальна енергія. Її можна розрахувати за формулою: $$ U=mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підйому.

Саме на збільшення потенціальної енергії буде витрачено \(1\ \text{%}\) енергії охолодження:

Відповідь: 0,76.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці. Ізопроцеси.

Завдання скеровано на перевірку вміння розв’язувати термодинамічні задачі з використанням графіка.

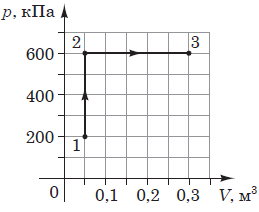
Рис. 1. Умова задачі

За рисунком можна визначити об’єм і тиск для всіх трьох точок процесу.

Дано:
\(p_1=200\ \text{кПа}\)
\(V_1=0,05\ \text{м}^3\)
\(p_2=600\ \text{кПа}\)
\(V_2=0,05\ \text{м}^3\)
\(p_3=600\ \text{кПа}\)
\(V_3=0,3\ \text{м}^3\)

Знайти:
\(A\ (\text{кДж})\ -\ ?\)

Перехід від стану 1 до стану 3 має два складники: ізохорне нагрівання, супроводжуване збільшенням тиску (1–2) та ізобарне розширення (2–3).

Робота в термодинамічному процесі виконується лише за зміни об’єму газу, тож в ізохорному процесі (1–2) робота не виконується.

Робота в ізобарному процесі (2–3) може бути обчислена за формулою $$ A=p\Delta V, $$ де \(p\) – тиск, \(\Delta V\) – зміна об’єму.

Тоді:

Відповідь: 150.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі пов'язані з поверхневим натягом та законами Ньютона.

Дано:
\(l=8\ \text{см}\)
\(m=0,48\ \text{г}\)
\(F=12\ \text{мН}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)

Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma} \left(\frac{\text{мН}}{\text{м}}\right)\ -\ ?\)

Для розв’язання задачі необхідно розуміти, які сили заважають підняти тонку дротинку з поверхні.

Зокрема на дротинку діє сила тяжіння, що притискає її до поверхні рідини: $$ F_\text{тяж}=mg. $$

Крім того дротик виділяє на поверхні рідини дві області – праворуч та ліворуч від себе. Тому з обох боків на нього діятимуть сили поверхневого натягу.

Силу поверхневого натягу можна розрахувати за формулою $$ F_\text{пов}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma} l. $$

Тоді сила, що необхідна для того, щоб підняти кільце з поверхні має подолати силу тяжіння і сили поверхневого натягу праворуч і ліворуч від дротика:

Тож тепер можна виразити поверхневий натяг із формули:

Відповідь: 45.

ТЕМА: Закони електролізу.

Завдання скеровано на перевірку вміння застосовувати закони електролізу для розв’язування розрахункових задач.

Дано:
\(S=120\ \text{см}^2\)
\(t=2\ \text{год}\)
\(I=0,3\ \text{А}\)
\(k=3\cdot 10^{-7}\ \frac{\text{кг}}{\text{Кл}}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=9\ \frac{\text{г}}{\text{см}^3}\)

Знайти:
\(d (\text{мкм})\ -\ ?\)

Нікелювання здійснюють електролізом. За першим законом електролізу можна визначити масу нікелю, що виділився:

За відомою масою \(m\) і густиною матеріалу \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\), то можна обчислити його об’єм: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV\rightarrow V=\frac{m}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}}. $$ Об’єм матеріалу можна виразити через товщину та площу його поверхні: $$ V=Sd\rightarrow d=\frac VS. $$

Тож, товщина матеріалу

Відповідь: 6.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на пошук частоти коливань.

Дано:
\(N=16\)
\(t=4\ \text{с}\)

Знайти:
\(v(\text{Гц})\ -\ ?\)

Частоту коливання тіла можна обчислити за формулою $$ v=\frac Nt=\frac{16}{4\ \text{с}}=4\ \text{с}^{-1}. $$

Переведімо частоту в герци, для цього пригадаймо, що: $$ 1\ \text{с}^{-1}=1\ \text{Гц}. $$

Тобто $$ 4\ \text{с}^{-1}=4\ \text{Гц}. $$

Відповідь: 4.

ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.

Дано:
\(W_{\text{конденсатора}\ max}=60\ \text{мДж}\)
\(W_\text{конденсатора}=2W_\text{котушки}\)

Знайти:
\(W_\text{конденсатора}(\text{мДж})\ -\ ?\)

У коливальному контурі під час незгасних коливань енергія переходить від конденсатора до котушки. Повна енергія системи є сталою, її визначають за формулою $$ W=W_\text{конденсатора}+W_\text{котушки} $$

Енергія конденсатора визначають за формулою $$ W_\text{конденсатора}=\frac{q^2}{2C}, $$ де \(q\) – заряд на обкладинках конденсатора, а \(C\) – ємність конденсатора.

Енергію котушки можна визначити за формулою $$ W_\text{котушки}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.

Максимальною енергія конденсатора буде в момент, коли він повністю заряджений. Цієї миті в котушці немає струму, тож її енергія дорівнює нулю.

Оскільки енергія в коливальному контурі за незгасних коливань зберігається, то $$ W=W_{\text{конденсатора}\ max} $$

Тоді для моменту, коли енергія електричного поля вдвічі більша за енергію магнітного поля котушки

Відповідь: 40.

ТЕМА: Оптика. Лінза. Формула тонкої лінзи.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосування законів геометричної оптики й формули тонкої лінзи.

Дано:
\(D=5\ \text{дптр}\)
\(d=1\ \text{м}\)

Знайти:
\(f(\text{м})\ -\ ?\)

Оптична сила пов’язана з фокусною відстанню лінзи \(F\): $$ D=\frac 1F. $$

Фокусну відстань лінзи та її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи $$ \frac 1F=\frac 1d+\frac 1f, $$ де \(d\) – відстань від об’єкта до лінзи, а \(f\) – відстань від лінзи до зображення, \(F\) – фокусна відстань лінзи.

Тоді можна виразити з формули тонкої лінзи відстань між лінзою і зображенням:

Відповідь: 0,25.

ТЕМА: Квантова фізика. Світлові кванти.

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі з використанням співвідношень квантової фізики та виразів для визначення потужності.

Дано:
\(N=5\cdot 10^{15}\ \text{с}^{-1}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=450\ \text{нм}\)
\(h=6,6\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\)
\(c=3\cdot 10^{8}\ \frac{\text{м}}{\text{с}}\)

Знайти:
\(P\ (\text{мВт})\ -\ ?\)

Потужність лазера можна визначити як відношення випроміненої енергії \(E\) до часу \(t\): $$ P=\frac Et. $$

Випромінену енергію можна знайти як суму енергії всіх випромінених фотонів за проміжок часу \(t\): $$ E=NE_0t, $$ де \(E_0\) – енергія одного випроміненого фотона, \(N\) – кількість випромінених фотонів.

Енергія фотона пов’язана з його довжиною хвилі: $$ E_0=\frac{hc}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}, $$ де \(h\) – стала Планка, \(c\) – швидкість світла у вакуумі, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) – довжина хвилі випромінювання.

Тоді маємо рівняння для потужності:

Відповідь: 2,2.