НМТ онлайн 2023 року з фізики – демоваріант

ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.

Завдання скеровано на перевірку розуміння поняття «механічна робота».

Механічна робота (робота сили) \(A\) ‒ це фізична величина, якою характеризують зміну механічного стану тіла. Механічна робота дорівнює добутку модуля сили \(F,\) модуля переміщення \(s\) і косинуса кута \(\mathbf{\alpha}\) між вектором сили та вектором переміщення: $$ A=Fs\cos\mathbf{\alpha}. $$

Сила тяжіння діє на літак і напрямлена вертикально вниз. Але переміщення літака по вертикалі немає. За умовою літак рухається горизонтально. Отже, кут між вектором сили тяжіння та вектором переміщення дорівнює \(90^\circ.\) Косинус кута \(90^\circ\) дорівнює нулю (див. рисунок). Відповідно робота сили тяжіння дорівнюватиме нулю, сила тяжіння не виконує роботу.

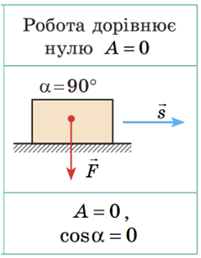
Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Кінетична і потенціальна енергія.

Завдання скеровано на перевірку вміння обчислювати імпульс тіла і його кінетичну енергію.

Імпульс тіла \(\overrightarrow{p}\) ‒ це векторна фізична величина, яка дорівнює добутку маси \(m\) тіла на швидкість \(\overrightarrow{v}\) його руху: $$ \overrightarrow{p}=m\overrightarrow{v}. $$

Обчислімо значення імпульсу тіла:

Кінетична енергія \(E_k\) ‒ це фізична величина, якою характеризують механічний стан рухомого тіла. Кінетична енергія дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху:

Обчислімо кінетичну енергію автомобіля:

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=const, $$ де \(p\) ‒ тиск, \(V\) ‒ об’єм, \(T\) ‒ абсолютна температура.

Графік 1 відповідає ізохорному охолодженню (\(V=const\) ‒ графік паралельний осі абсолютної температури, температура \(T\) під час цього знижується).

Графік 3 відповідає ізотермічному стисканню (\(T=const\) ‒ графік паралельний осі об’єму, під час цього об’єм зменшується).

Під час процесів 2 і 4 змінюються і об’єм, і температура. Під час процесу 4 хоча температура й знижується, але об’єм збільшується, тому тиск також знижуватиметься. Отже, цей процес не може бути ізобарним.

Графік 2 відповідає ізобарному охолодженню (об’єм зменшується пропорційно до зниження температури, отже, \(p=const).\)

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Насичена і ненасичена водяна пара, їхні властивості.

Завдання скеровано на перевірку розуміння, що таке насичена і ненасичена водяна пара, а також на обізнаність щодо принципу будови й дії приладу для вимірювання відносної вологості.

Пару, яка перебуває в стані динамічної рівноваги зі своєю рідиною, називають насиченою парою. Динамічна рівновага встановиться між процесами конденсації і випаровування, коли кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Концентрація молекул насиченої пари ‒ найбільша можлива концентрація молекул пари за певної температури.

Дія психрометра, приладу для вимірювання вологості повітря, базується на тому, що
1) швидкість випаровування рідини то вища, що нижча відносна вологість повітря;
2) рідина під час випаровування охолоджується.

Психрометр складений із двох термометрів ‒ сухого і вологого. Сухим термометром вимірюють температуру довкілля. Колба вологого термометра обгорнута тканиною, кінчик якої занурено в посудину з водою (див. рисунок). Вода з тканини випаровується, тому вологий термометр показує нижчу температуру, ніж сухий. Що нижча відносна вологість повітря, то швидше випаровується рідина й то більша різниця показів сухого і вологого термометрів.

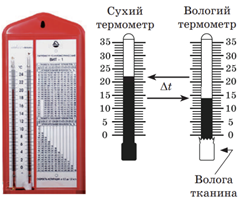
Пов’яжімо тепер насиченість водяної пари і вологість повітря. Відносна вологість показує, наскільки водяна пара близька до насичення. Тобто що менша різниця показів сухого і вологого термометрів психрометра, то водяна пара ближче до насичення.

У прикладі 1 є різниця між температурами термометрів, отже, пара точно не насичена. А у прикладі 2 термометри показують однакову температуру. Це означає, що за даної температури відносна вологість дорівнює \(100\ \text{%}\), тобто водяна пара в повітрі є насиченою.

Якщо температура повітря стає нижчою від точки роси (від температури, за якої водяна пара, що міститься в повітрі, стає насиченою), то водяна пара конденсується на різних поверхнях. У прикладі 3 водяна пара сконденсувалася на холодніших стінках ванної кімнати, утворилися крапельки роси, тобто пара у ванній кімнаті є насиченою.

Калюжі води на поверхні асфальту швидко висихають, тому що немає динамічної рівноваги між процесами конденсації і випаровування: кількість молекул, які повертаються в калюжу, значно менша за кількість молекул, які за той самий час випаровуються з поверхні калюжі. Водяна пара над калюжею буде ненасиченою.

Отже, умову завдання задовольняють приклади 2 і 3.

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.

Завдання скеровано на перевірку знання і розуміння характеристик електричного поля ‒ напруженості, потенціалу.

Однорідне електричне поле спричиняє перерозподіл електричних зарядів у провіднику, унаслідок чого на поверхні провідника виникають електричні заряди. Це явище електростатичної індукції. Індуковані заряди, що виникли, створюють власне електричне поле, напруженість якого напрямлена в бік, протилежний напруженості зовнішнього поля.

Перерозподілення зарядів у провіднику триватиме до моменту, коли створюване індукованими зарядами поле всередині провідника повністю компенсує зовнішнє поле. За дуже малий інтервал часу напруженість результувального поля всередині провідника дорівнюватиме нулю.

Одна з електростатичних властивостей провідників постулює, що поверхня провідника є еквіпотенціальною (в усіх точках такої поверхні значення потенціалу електростатичного поля однакове). Це твердження є прямим наслідком зв’язку між напруженістю \(E\) поля і різницею потенціалів \((\mathbf{\varphi}_1-\mathbf{\varphi}_2)\) $$ E=\frac{\mathbf{\varphi}_1-\mathbf{\varphi}_2}{d}, $$ де \(\mathbf{\varphi}_1\) ‒ потенціал у точці 1, \(\mathbf{\varphi}_2\) ‒ потенціал у точці 2, \(d\) ‒ відстань між точками 1 і 2.

Якщо напруженість поля всередині провідника дорівнює нулю, то різниця потенціалів також дорівнює нулю, тому потенціали в усіх точках провідника є однаковими.

Відповідь: A.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Закони електролізу.

Завдання скеровано на перевірку знання і розуміння законів Фарадея для електролізу.

Відповідно до першого закону Фарадея для електролізу маса \(m\) речовини, яка виділяється на електроді під час електролізу, прямо пропорційна силі струму \(I\) й часу \(t\) проходження його через електроліт: $$ m=kIt, $$ де \(k\) ‒ коефіцієнт пропорційності, який називають електрохімічним еквівалентом.

За умовою завдання силу струму збільшили втричі, а час електролізу зменшили в \(6\) разів: $$ m'=k\cdot 3I\cdot\frac t6=\frac 12kIt=\frac 12 m. $$

Отже, після змін фізичних величин маса речовини, що виділяється на електроді, зменшиться вдвічі.

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік.

Завдання скеровано на перевірку розуміння суті магнітного потоку й параметрів, від яких він залежить.

Кількість ліній магнітної індукції, що пронизують певну поверхню (у цьому завданні – поверхню, обмежену плоским дротяним кільцем), називають потоком магнітної індукції або магнітним потоком.

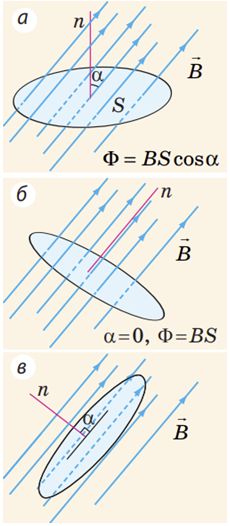
Розгляньмо плоский замкнений контур у магнітному полі. Нормаль \(n,\) проведена до поверхні, обмеженої контуром, утворює кут \(\mathbf{\alpha}\) з вектором магнітної індукції \(\overrightarrow{B}\) (рис. a).

Потік магнітної індукції (магнітний потік) \(\mathrm{Φ}\) ‒ це фізична величина, яка дорівнює добуткові магнітної індукції \(B\) на площу \(S\) поверхні та на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю до поверхні: $$ \mathrm{Φ}=BS\cos\mathbf{\alpha}. $$

Магнітний потік буде максимальним, якщо поверхня перпендикулярна до ліній магнітної індукції (рис. б), і дорівнюватиме нулю, якщо поверхня паралельна цим лініям (рис. в).

Залізо ‒ феромагнетик, намагнічується під дією зовнішнього магнітного поля, створює власне сильне магнітне поле, напрямлене в бік зовнішнього магнітного поля. Залізне осердя, розташоване в кільці, що проводить струм, значно посилить магнітну дію дротяного кільця. Отже, осердя впливатиме на зміну магнітного потоку.

Зминання кільця приводить до зміни площі поверхні, через яку проходить магнітний потік, прямо пропорційний цій площі.

Якщо повернемо кільце навколо осі, перпендикулярної до площини кільця (ця вісь збігається з нормаллю або паралельна їй, як показано на рис. a), то на зовнішнє магнітне поле це не вплине, площа поверхні, обмеженої кільцем, кут між нормаллю і вектором магнітної індукції не зміняться. Отже, такою дією магнітний потік змінити не можна.

Якщо ж повернути кільце навколо осі, що проходить у його площині, зміниться кут між нормаллю і вектором магнітної індукції, і, відповідно, магнітний потік.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Довжина хвилі.

Завдання скеровано на перевірку знання і розуміння поняття довжини хвилі й уміння визначати її за графіком.

Довжина хвилі \(\mathbf{\lambda}\) ‒ це відстань між двома найближчими точками, які коливаються однаково (синхронно). Якщо зафіксувати певний момент часу, то через відстань, яка дорівнює довжині \(\mathbf{\lambda}\) хвилі, форма хвилі повториться.

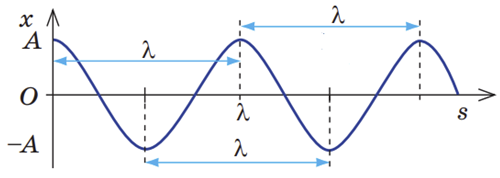
Розгляньмо рисунок в умові завдання. Виберімо точки, що рухаються синхронно.

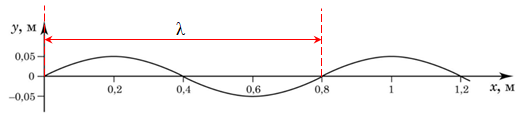
Отже, довжина хвилі, як видно з графіка, дорівнює \(0,8\ \text{м}.\)

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Закони заломлення світла.

Завдання скеровано на перевірку знання і розуміння законів заломлення світла.

Світловий промінь 1 проходить через межу в середовище 2, змінюючи, зазвичай, напрямок (див. рисунок). Отже, твердження A – неправильне.

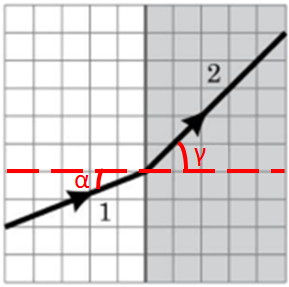
Зміну напрямку поширення світла в разі його проходження через межу поділу двох середовищ називають заломленням світла. Промінь 2, який задає напрямок заломленого пучка світла, називають заломленим променем. Кут \(\mathbf{\alpha}\) між падаючим променем 1 і перпендикуляром до межі поділу двох середовищ називають кутом падіння. Кут \(\mathbf{\gamma},\) утворений заломленим променем 2 і перпендикуляром до межі поділу двох середовищ, проведеним із точки падіння променя, називають кутом заломлення. З рисунка видно, що кут падіння менший за кут заломлення, отже, твердження Б є неправильним.

Оскільки кут падіння менший за кут заломлення, то це означає, що промінь переходить з оптично густішого середовища в оптично менш густе. І тоді швидкість світла в середовищі 1 менша, ніж у середовищі 2. Твердження В ‒ правильне.

Під час переходу з одного середовища в інше швидкість \(v\) поширення світла змінюється, але частота \(\mathbf{\nu}\) світлової хвилі, і, відповідно, колір світла залишаються незмінними. За формулою хвилі \(v=\mathbf{\lambda}\mathbf{\nu}\) змінюється довжина \(\mathbf{\lambda}\) світлової хвилі. Під час переходу в середовище 2 з меншою оптичною густиною довжина хвилі, як і її швидкість, збільшується: $$ \frac{v_1}{v_2}=\frac{\mathbf{\lambda}_1}{\mathbf{\lambda}_2}. $$

Тобто твердження Г – неправильне.

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Застосування фотоефекту в техніці.

Завдання скеровано на перевірку розуміння суті фотоефекту й уміння застосовувати знання про це явище.

Супроводжувану випромінюванням (емісією) електронів взаємодію світла з речовиною називають фотоефектом.

Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул й атомів, залишаються всередині тіла.

Фотоефект широко застосовують у пристроях для перетворення світлових сигналів на електричні або для безпосереднього перетворення світлової енергії на електричну.

Відповідь: A.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерна модель атома.

Завдання скеровано на перевірку вміння аналізувати склад ядра атома.

Атомне ядро утворюють нуклони: позитивно заряджені протони й електронейтральні нейтрони. Сумарну кількість протонів і нейтронів в атомі називають нуклонним або масовим числом і позначають буквою \(\mathrm{A}.\)

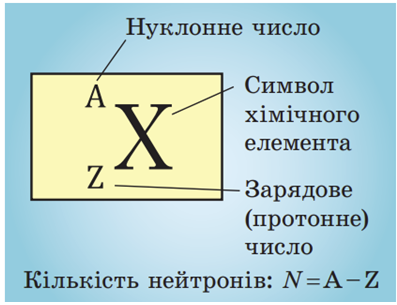
Кількість протонів у ядрі називають зарядовим або протонним числом і позначають буквою \(\mathrm{Z}.\) Порядковий номер хімічного елемента в періодичній системі дорівнює кількості протонів у ядрі (зарядовому числу).

Отже, у ядрі атома Урану \(_{\ \ 92}^{235}\mathrm{U}\) кількість нуклонів дорівнює \(235.\)

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика.

Завдання скеровано на перевірку розуміння явищ хвильової оптики й застосування їх у різних галузях.

1. Інтерференція ‒ явище накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.

Світлова хвиля частково відбивається від зовнішньої поверхні плівки, частково проходить через плівку й відбивається від її внутрішньої поверхні. Між ними є різниця ходу. Обидві хвилі когерентні, адже створені одним джерелом, тому внаслідок накладання їх спостерігають стійку інтерференційну картину.

Саме інтерференцією світла зумовлений колір багатьох комах. Плівки різної товщини райдужно забарвлені – мильні бульбашки, оліїста плівка на поверхні води тощо (B).

2. Явище обгинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики називають дифракцією. Дифракція властива будь-яким хвилям незалежно від їхньої природи. Особливо помітна дифракція на перешкодах, розмір яких набагато менший від довжини хвилі. Саме це заважає побачити атом за допомогою оптичного мікроскопа: адже розмір атома приблизно у \(1000\) разів менший від довжини хвилі світла. Світлові хвилі легко огинають атом, так ніби його й немає на шляху світла (Б).

3. Явище розкладання світла в спектр, зумовлене залежністю абсолютного показника заломлення середовища від частоти світлової хвилі, називають дисперсією світла. Веселка – це атмосферне оптичне явище, яке спостерігають унаслідок освітлення Сонцем безлічі водяних крапельок (дощу, туману тощо). Крапельки води по-різному відхиляють світло різних кольорів, тому біле світло розкладається на спектр (Г).

4. Світло ‒ поперечна хвиля. Поляризація світла ‒ це виділення у світловій хвилі коливань лише в одній площині або в кількох визначених. Поляризацію світла застосовують для створення об’ємного зображення в 3D-кінотеатрах. Цього досягають за допомогою окулярів із поляризаційними плівками. Поляризаційну плівку також наклеюють на екран, з якого транслюють зображення. Поляризаційна плівка на екрані розбиває цілісну картину на дві, формуючи стереопару. Унаслідок цього крізь спеціальні окуляри одне око бачить лише парні, а друге – тільки непарні рядки. Завдяки бінокулярності зору людський мозок може сумістити ці два зображення в одне. Невелика відстань між очима забезпечує незначну відмінність між обома картинками, тож цілісне зображення набуває об’ємності (А).

Відповідь: 1В, 2Б, 3Г, 4А.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Атом та атомне ядро.

Завдання скеровано на перевірку знання і розуміння важливих фізичних відкриттів.

1. Явище радіоактивності випадково відкрив 1896 року Анрі Антуан Беккерель. Він виявив, що сіль Урану самочинно випускає невидимі промені, які засвічують світлочутливі матеріали (фотопластинки) навіть у повній темряві. Згодом таке випромінювання назвали радіоактивним (Г).

2. У 1908–1911 рр. під керівництвом Ернеста Резерфорда науковці досліджували будову атома. Вони спрямовували на тонку золоту фольгу вузький пучок \(\mathbf{\alpha}-\text{частинок}\) зі свинцевого контейнера. Виявили, що переважна більшість \(\mathbf{\alpha}-\text{частинок}\) проходить крізь фольгу, не змінюючи напрямку руху, лише деякі відхиляються від початкової траєкторії. Приблизно одна з \(20\ 000\) частинок відскакувала від фольги, начебто натикаючись на якусь перешкоду. За результатами дослідів Резерфорд запропонував ядерну (планетарну) модель будови атома:

• в атомі позитивно заряджене ядро оточене негативно зарядженими частинками ‒ електронами, які обертаються навколо ядра, як планети навколо Сонця;
• саме в ядрі зосереджена мало не вся маса атома (A).

3. Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подається напруга від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту (В).

4. Досліди з вивчення природи радіоактивного випромінювання показали, що різні радіонукліди можуть випромінювати промені трьох видів:
1) \(\mathbf{\alpha}-\text{випромінювання}\) ‒ позитивно заряджені важкі частинки (ядра атомів Гелію);
2) \(\mathbf{\beta}-\text{випромінювання}\) ‒ негативно заряджені легкі частинки (швидкі електрони) й позитивно заряджені легкі частинки (швидкі позитрони);
3) \(\mathbf{\gamma}-\text{випромінювання}\) ‒ високочастотні електромагнітні хвилі.

Один із таких дослідів полягає в тому, що пучок радіоактивного випромінювання потрапляє спочатку в сильне магнітне поле постійного магніту, а потім – на фотопластинку. Після проявлення фотопластинки на ній чітко видно три темні плями, які свідчать про те, що урановий зразок висилає промені трьох видів. Магнітне поле по-різному діє на частинки різних знаків, або \((\mathbf{\gamma}-\text{випромінювання})\) не діє взагалі (Б).

Відповідь: 1Г, 2А, 3В, 4Б.

ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного і рівноприскореного рухів.

Розгляньмо рух парашутиста й монети.

За умовою завдання парашутист опускається зі сталою швидкістю \(v=5\ \text{м/с},\) оскільки дія сили тяжіння скомпенсована дією сили опору повітря. Отже, відстань \(h=100\ \text{м}\) він пройде за \(20\ \text{с}:\) $$ t_\text{пар} =\frac hv=\frac{100}{5}=20\ \text{с}. $$

Монета пройде той самий шлях \(h=100\ \text{м},\) але рухатиметься рівноприскорено. Початкова швидкість монети відносно парашутиста дорівнює нулю, оскільки вона просто випала з кишені. Оскільки монета випала з кишені парашутиста, який рухався зі швидкістю \(5\ \text{м/с},\) початкова швидкість монети відносно поверхні землі дорівнює \(v_0=5\ \text{м/с}.\) Вплив опору повітря на монету за умовою не враховуємо, тож знайдімо час її падіння з кінематичного рівняння: $$ h=v_0t+\frac{>^2}{2}, $$ (\(g\) ‒ прискорення вільного падіння; усі векторні величини записані у проекціях на вісь \(Oy,\) яка напрямлена вертикально вниз, так само, як і вектор прискорення вільного падіння).

Підставмо значення величин у рівняння: $$ h=v_0t+\frac{>^2}{2}\Rightarrow 100=5t+\frac{10t^2}{2}. $$

Поділімо ліву і праву частини рівняння на \(5\) й отримаємо зведене квадратне рівняння: $$ t^2+t-20=0. $$

За теоремою Вієтта визначмо корені рівняння: \(t_1=-5,\ \ t_2=4.\)

Час не може бути від’ємним, умову завдання задовольняє корінь \(t_2=4\ \text{с},\) тобто монета впала за \(4\ \text{с},\) а парашутист, відповідно, приземлився на \(16\ \text{с}\) пізніше: $$ \Delta t=t_\text{пар}-t_2=20\ \text{с}-4\ \text{с}=16\ \text{с}. $$

Відповідь: 16.

ТЕМА: Механіка. Основи динаміки. Момент сили. Умови рівноваги тіла.

Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла на прикладі простого механізму ‒ важеля.

Якщо тіло може тільки обертатися (має нерухому вісь обертання), то за правилом моментів воно перебуває в рівновазі, якщо алгебраїчна сума моментів сил, що діють на тіло, дорівнює нулю: $$ M_1+M_2+\cdots+M_n=0. $$

Момент сили \(M\) ‒ це фізична величина, яка дорівнює добутку модуля сили \(F,\) яка діє на тіло, на плече \(d\) цієї сили: $$ M=F\cdot d. $$

Плече \(d\) сили \(F\) ‒ це найменша відстань від осі обертання тіла до лінії, уздовж якої діє сила \(\overrightarrow{F}.\) Якщо сила обертає тіло проти ходу годинникової стрілки ‒ момент такої сили вважають додатним. Якщо сила обертає (або намагається обертати) тіло за ходом годинникової стрілки, то момент такої сили вважають від’ємним.

Запишімо правило моментів відповідно до умови завдання, урахувавши знаки моментів сил. Для цього спочатку позначмо на рисунку сили і плечі цих сил.

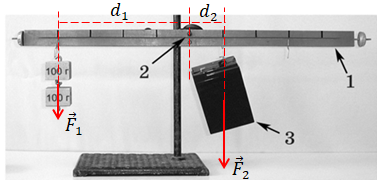
Сили \(\overrightarrow{F}_1\) і \(\overrightarrow{F}_2\) ‒ це сили тяжіння, що відповідно діють на важки масою \(100\ \text{г}\) кожен і на вантаж \(3.\) Бачимо з рисунка, що важіль поділений на одиничні відрізки, кожен із яких нехай дорівнює \(x.\) Тоді плече \(d_1=4x,\) а плече \(d_2=x.\) Звідси $$ 2mg\cdot 4x=Mg\cdot x, $$ де \(m\) ‒ маса одного важка \(100\ \text{г},\) \(M\) ‒ маса вантажу \(3,\) яку треба обчислити, \(g\) ‒ прискорення вільного падіння; \begin{gather*} 8m=M,\\[7pt] M=8\cdot 0,1\ \text{кг}=0,8\ \text{кг}. \end{gather*} Отже, маса вантажу \(3\) дорівнює \(0,8\ \text{кг}.\)

Відповідь: 0,8.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Принцип дії теплових двигунів. Коефіцієнт корисної дії і його максимальне значення.

Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати коефіцієнт корисної дії різними способами.

Коефіцієнт корисної дії (ККД) \(\mathbf{\eta}\) ‒ фізична величина, якою характеризують економічність теплового двигуна. Він дорівнює відношенню роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \mathbf{\eta}=\frac AQ. $$

Аналізуючи роботу теплових двигунів, французький інженер Саді Карно дійшов висновку, що найефективнішим \((\)із максимально можливим коефіцієнтом корисної дії \(\mathbf{\eta}_{max})\) є ідеальний тепловий двигун, який працює за циклом із двох ізотермічних і двох адіабатних процесів. Карно довів, що ККД такого двигуна дорівнює: $$ \mathbf{\eta}_{max}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівника; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняймо ці два вирази: \begin{gather*} \frac AQ=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}},\\[6pt] Q=\frac{A\cdot T_\text{Н}}{T_\text{Н}-T_\text{Х}}. \end{gather*}

Перш ніж виконати обчислення кількості теплоти від нагрівника, переведемо температуру в кельвіни:

Відповідь: 8.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.

Завдання скеровано на перевірку розуміння послідовного і паралельного з’єднань провідників і відповідних їм фізичних величин, умінь описувати аналітично схеми (ділянки схем) електричного кола й застосовувати закон Ома для ділянки кола.

Напруга на кінцях зображеної на рисунку ділянки електричного кола складається з напруги на першому резисторі й напруги на ділянці паралельно з’єднаних резисторів 2 і 3, тому що резистор 1 і ділянка кола з резисторами 2 і 3 з’єднані послідовно. Обчислімо зазначені напруги, і тоді зможемо визначити загальну напругу на зображеній ділянці.

Почнімо з резистора 3: відомий його опір і сила струму, яку показує амперметр. За законом Ома для ділянки кола ми можемо обчислити напругу на цьому резисторі: $$ U_3=I_3\cdot R_3=0,2\ \text{А}\cdot 20\ \text{Ом}=4\ \text{В}. $$

Напруга на кожному з паралельно з’єднаних провідників є однаковою: $$ U_3=U_2=4\ \text{В}. $$

За значеннями напруги на резисторі 2 та його опору можемо обчислити силу струму, що проходить крізь резистор 2: $$ I_2=\frac{U_2}{R_2}=\frac{4\ \text{В}}{5\ \text{Ом}}=0,8\ \text{А}. $$ (Дійсно, опори резисторів 2 і 3 відрізняються в \(4\) рази, отже, і сили струму відрізнятимуться в \(4\) рази ‒ обернена залежність).

Отже, загальний струм у ділянці кола \(I_1,\) тобто струм, що проходитиме крізь резистор 1, дорівнюватиме сумі струмів \(I_2\) і \(I_3\) після розгалуження: $$ I_1=I_2+I_3=0,8\ \text{А}+0,2\ \text{А}=1\ \text{А}. $$

Визначаємо напругу на резисторі 1: $$ U_1=I_1\cdot R_1=1\ \text{А}\cdot 6\ \text{Ом}=6\ \text{В}. $$

Обчислюємо загальну напругу на зображеній ділянці електричного кола: $$ U=U_1+U_2=6\ \text{В}+4\ \text{В}=10\ \text{В}. $$

Відповідь: 10.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона. Електромагнітні хвилі та швидкість поширення їх. Електродинаміка. Основи електростатики. З’єднання конденсаторів.

Завдання скеровано на перевірку розуміння принципу роботи коливального контуру.

Радіохвилі ‒ це електромагнітні хвилі, які поширюються із швидкістю світла \(c.\)

Довжину хвилі \(\mathbf{\lambda}\) визначмо за формулою $$ \mathbf{\lambda}=cT, $$ де \(T\) ‒ період власних електромагнітних коливань у коливальному контурі. Його можна визначити за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.

Отже, довжину хвилі, на яку налаштовано радіоприймач, обчислімо за формулою: $$ \mathbf{\lambda}_1=c\cdot 2\mathbf{\pi}\sqrt{LC_1}. $$

Після приєднання паралельно до конденсатора ще одного, утричі більшої ємності, загальна електроємність дорівнюватиме: \begin{gather*} C_2=C_1+3C_1=4C_1, \end{gather*} бо за паралельного з’єднання конденсаторів їхні електроємності додають одну до одної.

Тепер радіоприймач буде налаштований на довжину хвилі \(\mathbf{\lambda}_2:\) $$ \mathbf{\lambda}_2=c\cdot 2\mathbf{\pi}\sqrt{L4C_1}. $$

Поділімо ліві і праві частини формул для довжин хвиль:

Відповідь: 8.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.

Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння застосовувати формулу, якою описують цей закон.

Період піврозпаду \(T\) ‒ це фізична величина, що дорівнює часу, протягом якого розпадається половина наявної кількості ядер певного радіонукліда.

Основний закон радіоактивного розпаду описують формулою $$ N=N_0\cdot 2^{-\frac tT}, $$ де \(N\) ‒ кількість ядер радіонукліда, що залишились у зразку через час \(t;\) \(N_0\) ‒ початкова кількість ядер; \(T\) ‒ період піврозпаду; \(t\) ‒ час розпаду.

Виразімо кількість \(N\) ядер речовини через фізичні величини, дані в умові завдання ‒ масу \(m\) нукліда і його молярну масу \(M.\) Початкова кількість ядер \(N_0\) нукліда Натрію $$ N_0=\frac{m_1}{M}N_A. $$

Кінцева кількість ядер \(N\) нукліда Натрію $$ N=\frac{m_2}{M}N_A, $$ де \(N_А\) ‒ стала Авоґадро.

Підставмо ці вирази у формулу закону радіоактивного розпаду:

Підставмо числові дані з умови й обчислімо шуканий проміжок часу \(t:\)

Відповідь: 13.