НМТ онлайн 2023 року з фізики – 2 сесія
Тестові завдання другої сесії національного мультитесту (ЗНО) 2023 року з фізики
ТЕМА: Механіка. Основи кінематики. Траєкторія. Шлях і переміщення.
Завдання скеровано на перевірку знання і розуміння змісту понять шляху й переміщення.
Шлях
Переміщення
Згідно з умовою шлях утричі більший за модуль переміщення:
Розгляньмо кожен варіант відповіді.
A півколо
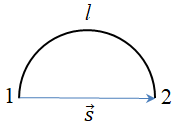
Шлях у цьому разі дорівнюватиме довжині півкола радіуса
Модуль переміщення дорівнюватиме подвійному радіусу ‒ діаметру цього кола:
Б дві сторони квадрата
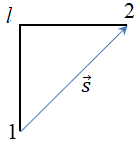
Шлях у цьому разі дорівнюватиме сумі довжин двох сторін
Модуль переміщення дорівнюватиме довжині діагоналі квадрата зі стороною
B відрізок
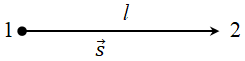
Шлях у цьому разі дорівнює модулю переміщення:
Г три сторони квадрата
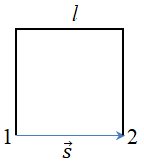
Шлях у цьому разі дорівнюватиме сумі довжин трьох сторін
Модуль переміщення дорівнюватиме довжині сторони квадрата зі стороною
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку вміння описувати рух аналітично.
За умовою швидкість під час прямолінійного руху тіла протягом усього часу збільшується, тобто тіло рухається прискорено.
Запишімо рівняння залежності координати
Варіанти відповіді
Розгляньмо рівняння
Розгляньмо рівняння
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння змісту поняття механічної роботи й умов виконання її.
Механічна робота (робота сили)
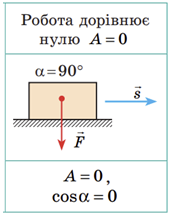
І з формули, і з рисунка випливає, що робота дорівнюватиме нулю, якщо кут між векторами сили й переміщення становить
За всіх інших значень кута
На книгу, що лежить на столі, сила тяжіння діє вертикально вниз, але книга перебуває в стані спокою відносно стола й переміщення не здійснює, тому що дія сили тяжіння скомпенсована дією сили нормальної реакції з боку стола. Тобто сила тяжіння роботу не виконує.
Крапелька води падає під час дощу, тобто здійснює переміщення саме під дією сили тяжіння, отже, сила тяжіння в цій ситуації виконує роботу.
Коли дерев’яна колода плаває на поверхні озера, дія сили тяжіння скомпенсована дією сили Архімеда, і колода у вертикальному напрямку не переміщається ‒ сила тяжіння роботу не виконує. Однак в умові зазначено, що колода плаває, тобто є горизонтальне переміщення, зумовлене не силою тяжіння. Тоді кут між векторами сили тяжіння і вектором переміщення становитиме
Єдина сила, яка діє на супутник під час руху коловою орбітою навколо Землі – це гравітаційна сила притягання Землі – сила тяжіння, що спрямована до центра Землі. Це означає, що супутник здійснює рівномірний рух по колу, його швидкість постійна, що дає змогу підтримувати незмінною відстань між супутником і центром Землі.
Згідно з теоремою про потенціальну енергію (робота всіх консервативних сил, які діють на тіло, дорівнює зміні потенціальної енергії тіла, узятій із протилежним знаком) зміни відстані між супутником і Землею не відбувається. Отже, зміна потенціальної енергії дорівнює нулю, сила тяжіння роботу не виконує.
Можна міркувати так: до вектора швидкості руху супутника в кожній точці колової орбіти, а також до вектора переміщення в кожній точці колової орбіти вектор сили тяжіння перпендикулярний, а
Отже, правильний варіант відповіді ‒ Б.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Температура. Рівняння стану ідеального газу. Ізопроцеси.
Завдання скеровано на перевірку розуміння поняття середньої кінетичної енергії хаотичного руху молекул, а також розуміння процесів, що відбуваються з газом.
Середня кінетична енергія
Також середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі
Під час ізохорного охолодження температура зменшуватиметься, відповідно середня кінетична енергія хаотичного руху молекул газу теж зменшуватиметься.
Ізотермічне стискання відбувається за сталої температури. Отже, середня кінетична енергія хаотичного руху молекул газу не зростатиме.
У ході адіабатного розширення, відповідно до першого закону термодинаміки, газ виконує додатну роботу внаслідок зменшення внутрішньої енергії, а температура газу зменшується. Тобто середня кінетична енергія хаотичного руху молекул газу зменшуватиметься.
Під час ізобарного розширення передана газу кількість теплоти витрачається і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Якщо збільшується внутрішня енергія, то й температура збільшуватиметься. Тому середня кінетична енергія хаотичного руху молекул газу зростатиме.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл.
Завдання скеровано на перевірку розуміння процесів переходу речовини з одного агрегатного стану в інший.
Плавлення ‒ це процес переходу речовини з твердого стану в рідкий.
Проаналізувавши наведений у завданні графік, можна дійти висновку, що протягом
Після досягнення температури
Уся енергія, що надходить від нагрівача, витрачається на руйнування кристалічних ґраток олова. У цей інтервал часу збільшення внутрішньої енергії олова триває.
Після того, як усе олово розплавиться, його температура починає зростати (ділянка від
Отже, під час плавлення температура олова не змінювалася (горизонтальна ділянка графіка), а це тривало відповідно до графіка від
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Енергія електричного поля.
Завдання скеровано на перевірку знання величин, від яких залежить енергія електричного поля конденсатора.
Енергію електричного поля
Якщо заряд конденсатора зменшили вдвічі, то
Отже, за незмінної електроємності (тому що зменшували заряд того самого конденсатора) енергія конденсатора залежить від зміни заряду.
Унаслідок зменшення заряду у
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у розчинах і розплавах електролітів.
Завдання скеровано на перевірку знання базових понять електролітичної дисоціації, рекомбінації, йонізації, фотоефекту й розуміння їхнього фізичного змісту.
Розпад молекул на йони під впливом полярних молекул розчинника називають електролітичною дисоціацією.
Наприклад, коли кристалик кухонної солі потрапляє у воду, полярні молекули води оточують йони Натрію і йони Хлору й відокремлюють їх від кристалика.
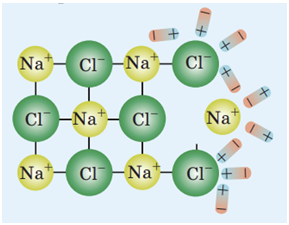
Унаслідок цього в розчині з’являються вільні заряджені частинки ‒ позитивні і негативні йони.
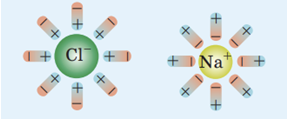
Злиття різнойменних йонів у молекулу чи кристал називають рекомбінацією йонів.
Утворення під впливом йонізатора позитивних і негативних йонів, а також, можливо, ще й вільних електронів із нейтральних молекул й атомів, називають йонізацією.
Вивільнення електронів речовини під дією електромагнітного випромінювання називають фотоефектом.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння визначення напрямку дії сили Лоренца.
Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца.
Напрямок сили Лоренца визначають за правилом лівої руки: лінії магнітної індукції
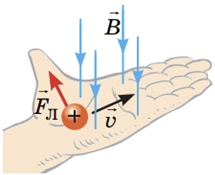
Отже, якщо людина розмістить долоню лівої руки відповідно до правила, великий палець буде напрямлений до неї перпендикулярно до площини рисунка. Це варіант відповіді B.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку вміння застосовувати рівняння гармонічних коливань і знання відповідних фізичних величин.
Коливання, під час яких координата
За умовою амплітуда коливань
Отже, із чотирьох рівнянь у варіантах відповіді умову задовольняють лише ті два, у яких множник біля функції синуса дорівнює
За умовою період коливань тіла
Тобто циклічна частота
Циклічна частота в рівнянні, записаному в загальному вигляді, є множником біля часу
Отже, усім параметрам відповідає рівняння
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку розуміння особливостей роботи навантаженого трансформатора й співвідношення величин, якими описують його роботу.
Якщо вторинну обмотку трансформатора замкнути на навантаження (підімкнути споживача ‒ наприклад, лампу), то в обмотці виникне електричний струм (див. рисунок).
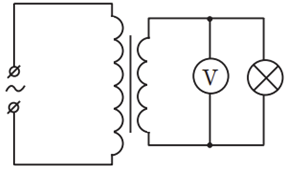
Цей струм спричинить зменшення магнітного потоку в осерді і, як наслідок, зменшення ЕРС (електрорушійної сили) самоіндукції в первинній обмотці. Унаслідок цього сила струму в первинній обмотці збільшиться і магнітний потік зросте до попереднього значення. Що більшими є сила струму у вторинній обмотці й потужність, яку трансформатор віддає споживачеві, то більшими є струм у первинній обмотці й потужність, яка надходить у трансформатор від джерела.
Під час роботи навантаженого трансформатора для відповідних значень напруги і сили струму справджується приблизна рівність:
Це означає, що в підвищувальному трансформаторі сила струму більша в первинній обмотці
Якщо трансформатор ідеальний (утрати енергії дорівнюють нулю), то в скільки разів він збільшує напругу, у стільки ж разів він зменшує силу струму, і навпаки.
За умовою трансформатор знижувальний ‒ у вторинній обмотці менше витків, ніж у первинній, отже, правильними є співвідношення
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.
Завдання скеровано на перевірку знання і розуміння наслідків постулатів спеціальної теорії відносності, зокрема того, який зв’язок між масою та енергією.
Будь-яке тіло (будь-яка частинка) масою
Дійсно, навіть якщо швидкість руху тіла (частинки) зменшується до нуля
За умовою газ унаслідок конвекції отримав ще кількість теплоти
Якщо тіло, навіть не рухаючись, має енергію
Отримавши ще енергію
Тобто маса тіла збільшилася на
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Запишімо рівняння ядерної реакції відповідно до умови завдання:
Порядковий номер елемента
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку розуміння руху тіла вздовж похилої площини під дією кількох сил.
Зобразімо схематично транспортер у вигляді похилої площини та брусок на ньому, що рухається вгору разом зі стрічкою транспортера зі швидкістю
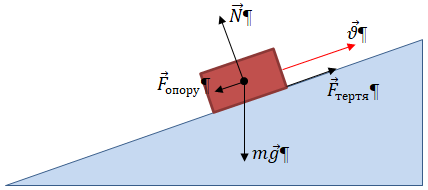
Сила тяжіння
Сила нормальної реакції
Брусок, рухаючись угору разом зі стрічкою транспортера, не зісковзує вниз завдяки силі третя
Сила опору
Відповідь: 1Д, 2Б, 3А, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект й експериментально встановлені його закони. Рівняння Ейнштейна для фотоефекту.
Завдання скеровано на перевірку знання, розуміння і застосування фізичних характеристик, рівняння Ейнштейна для фотоефекту, його законів.
1. Енергія
Якщо за умовою частоту світла, яке падає на поверхню металу, збільшили в
2. Довжину
Після збільшення частоти світла в
3. Робота виходу
Якщо ще збільшувати частоту світла, то збільшуватиметься не робота виходу (яка є конкретною для кожного металу), а максимальна початкова швидкість й кінетична енергія фотоелектронів.
Отже, робота виходу електрона з металу не зміниться (Д).
4. Запишімо рівняння Ейнштейна для фотоефекту за початкових умов (до зміни частоти):
Тоді рівняння для фотоефекту таке:
Запишімо рівняння Ейнштейна для фотоефекту, якщо частота світла збільшилася в
Перевіримо аналітично:
1) чи дійсно затримувальна напруга збільшиться;
2) якщо так, то в скільки разів
Поділимо рівняння одне на одне:
Отже, математично ми довели, що
Відповідь: 1Б, 2А, 3Д, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Рух тіла під дією кількох сил.
Завдання скеровано на перевірку вміння розв’язувати комбіновані завдання ‒ описати коливальний рух за допомогою другого закону Ньютона і закону збереження механічної енергії.
Спочатку скористаймося законом збереження механічної енергії. У момент проходження кулькою положення рівноваги модуль швидкості
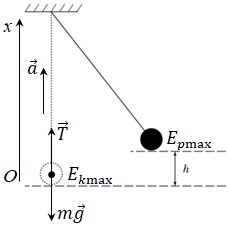
А коли кулька підіймається на максимальну висоту
Це формула для обчислення шуканої за умовою висоти. Але швидкість руху кульки невідома. Визначмо її, скориставшись другим законом Ньютона:
Тобто на кульку діє сила тяжіння
Оскільки, гойдаючись на нитці, кулька рухається по дузі кола, то прискорення
Знайдемо проєкції векторів усіх величин другого закону Ньютона на вісь
Виразимо звідси модуль швидкості руху
Підставимо це значення швидкості руху кульки у формулу для обчислення максимальної висоти її підйому:
Відповідь: 0,25.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку знання і вміння застосувати закон Архімеда.
Скористаймося законом Архімеда. На тіло, занурене в рідину або газ, діє виштовхувальна сила
Обчислимо значення сили Архімеда:
Відповідь: 20.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.
Завдання скеровано на перевірку розуміння першого закону термодинаміки стосовно ізобарного процесу.
У ході ізобарного процесу виконується робота
Під час ізобарного процесу передана газу кількість теплоти
а зміна його внутрішньої енергії
Кількість теплоти, передана газу, така:
Або
Виразімо з формули й обчислімо кількість речовини:
Відповідь: 6.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на перевірку знання закону Ома для ділянки кола й параметрів, від яких залежить електричний опір.
Електричний опір
Якщо не замінювати дріт, а брати лише його частину, то у формулі зміниться лише значення довжини дроту, а питомий опір і площа поперечного перерізу залишаться ті самі. Тобто опір провідника прямо пропорційний його довжині:
Отже, можна скласти пропорцію. Якщо дріт довжиною
Обчислимо опір ділянки дроту довжиною
За законом Ома для ділянки кола можна визначити силу струму в дроті, якщо за умовою вольтметр показує напругу
Відповідь: 0,5.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння будувати зображення в збиральній лінзі й уміння застосовувати формулу тонкої лінзи.
Побудуємо відповідно до умови завдання зображення, що дає збиральна лінза.
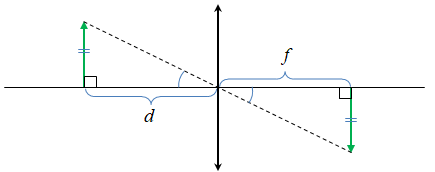
Побудувавши, отримуємо два рівні прямокутні трикутники – за катетом і гострим кутом: гострі кути рівні як вертикальні, катети рівні за умовою – предмет і його зображення однакового розміру.
Зваживши на це, запишімо формулу тонкої лінзи:
З рівності трикутників випливає, що
Обчислімо фокусну відстань лінзи:
Відповідь: 20.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Виразимо кількість ядер радіонукліда, що залишились у зразку, через початкову кількість ядер відповідно до умови завдання:
Підставимо всі дані у формулу:
Кількість атомів радіонукліда, що потрапили у водойму, зменшиться в
Відповідь: 150.
Знайшли помилку? Пишіть на




