НМТ онлайн 2024 року з фізики – 2 сесія

Коментар

ТЕМА: Механіка. Основи кінематики.

Завдання скеровано на перевірку знання і розуміння понять швидкості руху й прискорення та їхньої графічної інтерпретації.

Правильним є варіант відповіді А ‒ вектор миттєвої швидкості руху тіла напрямлений по дотичній до траєкторії руху.

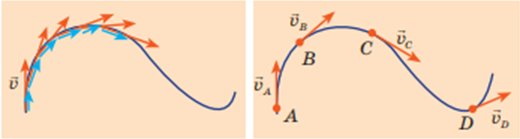
Розбиваючи траєкторію руху тіла на дедалі менші ділянки, бачимо, що вектор швидкості все більше наближається до дотичної. У кожній точці миттєва швидкість напрямлена вздовж дотичної до траєкторії руху тіла.

Твердження, що вектор прискорення тіла напрямлений по дотичній до траєкторії руху є хибним. Пряму, що проходить через точку кола або дуги перпендикулярно до радіуса, проведеного в цю точку, називають дотичною. Під час руху по колу або по дузі (криволінійний рух) прискорення буде напрямлене до центра кола, а не вздовж дотичної до нього. Якщо ж це буде прямолінійний рух, то вектор прискорення буде напрямлений вздовж траєкторії руху, але не по дотичній.

Вектор швидкості буде напрямлений по дотичній у разі руху по колу. Тоді кут між вектором швидкості й прискорення буде прямим. І це лише в разі руху по колу, а не для будь-якого механічного руху.

Якщо кут між векторами швидкості й прискорення дорівнює нулю, то це лише частинний випадок руху тіла прямолінійного й прискореного. Таке твердження не є правильним для будь-якого механічного руху.

Відповідь: A.

Коментар

ТЕМА: Механіка. Закони збереження в механіці. Потенціальна енергія.

Завдання скеровано на перевірку знання і розуміння залежності потенціальної енергії пружно деформованого тіла від видовження пружини.

Потенціальну енергію \(E_p\) пружно деформованого тіла визначаємо за формулою $$ E_p=\frac{kx^2}{2}, $$ де \(k\) ‒ жорсткість пружини, \(x\) ‒ видовження пружини.

Запишімо формули для обох випадків, що зазначені в умові:

\begin{gather*} E_{p1}=\frac{kx_1^2}{2},\\[6pt] E_{p2}=\frac{kx_2^2}{2}. \end{gather*}

За умовою \(E_{p1}=4\ \text{Дж},\) \(x_1=2\ \text{см}=0,02\ \text{м},\) \(x_2=4\ \text{см}=0,04\ \text{м}=2x_1:\)

Визначмо, на скільки збільшилася потенціальна енергія пружини, якщо її розтягнути вдвічі більше:

Відповідь: B.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основне рівняння молекулярно-кінетичної теорії.

Завдання скеровано на перевірку знання і розуміння поняття концентрації.

Концентрація \(n\) молекул газу ‒ фізична величина, яка дорівнює кількості \(N\) молекул в одиниці об’єму \(V\) газу: $$ n=\frac NV. $$

Кількість \(N\) молекул речовини визначають за формулою $$ N=\frac mM\cdot N_A, $$ де \(m\) ‒ маса речовини, \(M\) ‒ її молярна маса (тобто маса речовини кількістю \(1\) моль), \(N_A=6\cdot 10^{23}\ \text{моль}^{-1}\) ‒ стала Авогадро, тобто однакова кількість атомів або молекул в будь-якій речовині кількістю один моль.

Визначмо мінімальну небезпечну концентрацію атомів Меркурію в повітрі, користуючись даними задачі:

Відповідь: Б.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія та способи її зміни.

Завдання скеровано на перевірку знання і розуміння поняття внутрішньої енергії і причин її зміни.

Внутрішню енергію макроскопічного тіла визначає характер руху та взаємодії всіх мікрочастинок, з яких складається тіло (система тіл). Цю енергію в термодинаміці визначають як суму кінетичної енергії хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), з яких складається тіло, і потенціальної енергії їхньої взаємодії.

Внутрішня енергія \(U\) ідеального газу певної маси прямо пропорційна його абсолютній температурі \(T:\) $$ U\sim T. $$

Цю енергію можна змінити двома способами: виконанням роботи й теплопередачею.

Температура сковорідки, яку поставили на запалену конфорку, підвищуватиметься, тому її внутрішня енергія зростатиме.

У хлопчика змерзли руки. Щоб їх зігріти, він виконує роботу ‒ тре руки одна об одну. Тож внутрішня енергія збільшуватиметься.

Морозиво, яке дістали з морозильної камери, починає нагріватися від навколишнього повітря, тепла руки й теплого дихання дівчинки. Отже, внутрішня енергія морозива зростатиме внаслідок нагрівання.

Після прасування праску вимкнули з мережі. Тому праска почала остигати, оскільки тепло перестало виділятися після припинення проходження електричного струму. Отже, у цьому разі внутрішня енергія праски зменшуватиметься.

Відповідь: Г.

Коментар

ТЕМА: Електродинаміка. Основи електростатики. Провідники та діелектрики в електростатичному полі.

Завдання скеровано на перевірку знання і розуміння електростатичних властивостей провідників.

І. Під дією електростатичного поля рух вільних електронів стає напрямленим. Електрони не можуть залишити провідник і накопичуються в певній області його поверхні, ‒ ця область поверхні провідника набуває негативного заряду; протилежна ‒ позитивного (його створюють позитивні йони, що там залишилися). Тому на поверхні провідника з’являються наведені (індуковані) електричні заряди за незмінного сумарного заряду провідника.

Індуковані заряди, що виникли, створюють власне електричне поле напруженістю \(\overrightarrow{E}',\) яка напрямлена в бік, протилежний напруженості \(\overrightarrow{E}_0\) зовнішнього поля (див. рисунок).

$$ E=E_0-E'. $$

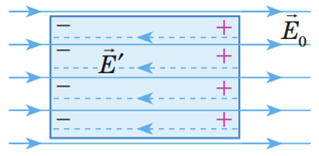
Процес перерозподілу зарядів у провіднику триватиме до моменту, коли створюване індукованими зарядами поле всередині провідника повністю компенсує зовнішнє поле. За дуже малий інтервал часу напруженість $$ \overrightarrow{E}=\overrightarrow{E}_0+\overrightarrow{E}' $$ результувального поля всередині провідника дорівнюватиме нулю. Це твердження щодо електростатичної властивості провідника правильне.

ІІ. Еквіпотенціальна поверхня ‒ це поверхня, в усіх точках якої потенціал електростатичного поля має однакове значення. Поверхня провідника є еквіпотенціальною. Це твердження є прямим наслідком зв’язку між напруженістю \(E\) поля і різницею потенціалів \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_1-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_2\) (де \(d\) ‒ відстань між точками \(1\) і \(2\)): $$ E=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_1-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_2}{d}. $$

Якщо напруженість поля всередині провідника дорівнює нулю, то різниця потенціалів також дорівнює нулю, тому потенціали в усіх точках провідника є однаковими. Твердження правильне.

ІІІ. Увесь статичний заряд провідника зосереджений на його поверхні. Ця властивість є наслідком закону Кулона і властивості однойменних зарядів відштовхуватися. Твердження правильне.

ІV. Оскільки зовнішнє електричне поле викликає появу індукованих зарядів тільки на поверхні провідника, а поля всередині провідника немає, то всередині провідника не можуть циркулювати постійні струми. Твердження неправильне.

Відповідь: B.

Коментар

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку знання і розуміння поняття потужності електричного струму і її залежності від параметрів електричного кола.

Потужність струму \(P\) ‒ фізична величина, яка чисельно дорівнює роботі струму за одиницю часу: $$ P=\frac At, $$ де \(A\) ‒ робота, виконана струмом за час \(t.\)

Виходячи з означення електричної напруги (електрична напруга на ділянці кола ‒ фізична величина, яка характеризує електричне поле на ділянці кола і чисельно дорівнює роботі електричного поля з переміщення по цій ділянці заряду \(1\) Кл) і зваживши на те, що \begin{gather*} A=UIt,\ \text{маємо:}\\[6pt] P=UI, \end{gather*} де \(U\) ‒ напруга на ділянці кола, на якій визначають потужність струму; \(I\) ‒ сила струму в ділянці.

Із закону Ома для ділянки кола \(\left(I=\frac UR\right)\) випливає, що $$ P=UI=\frac{U^2}{R}. $$

Запишемо формули для визначення потужності в обох випадках (за умовою \(R_1=R_2,\ U_2=2U_1\)): \begin{gather*} P_1=\frac{U_1^2}{R},\\[6pt] P_2=\frac{U_2^2}{R}=\frac{(2U_1)^2}{R}=\frac{4U_1^2}{R}=4P_1. \end{gather*}

Отже, потужність \(P_2\) постійного струму після збільшення напруги вдвічі на ділянці кола збільшиться вчетверо (у \(4\) рази).

Відповідь: Б.

Коментар

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у металах. Електричний струм у напівпровідниках.

Завдання скеровано на перевірку знання і розуміння властивостей електричного струму в різних середовищах, а саме в металах і напівпровідниках.

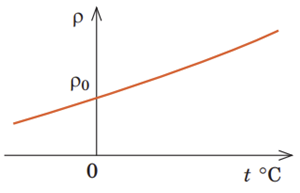
Як бачимо на рисунку 1, після замикання ключа амперметр зафіксував певне значення сили струму. Після нагрівання спіралі значення сили струму зменшилося (рис. 2). Це свідчить про те, що опір спіралі збільшився. Тож доходимо висновку, що спіраль зроблено з металу, оскільки саме для металів зі збільшенням температури характерне збільшення опору (позитивно заряджені йони у вузлах кристалічної ґратки починають коливатися з більшою амплітудою, і тому частіше зіштовхуються з вільними електронами, які створюють електричний струм, також активізується тепловий хаотичний рух самих вільних електронів і збільшується кількість зіткнень).

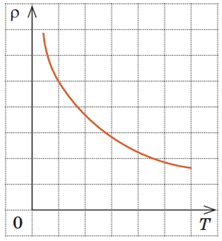
Опір напівпровідників із підвищенням температури зменшується (див. рисунок), оскільки збільшується кількість вільних електронів і дірок. Збільшиться, відповідно, і провідність напівпровідника, і сила струму.

Відповідь: B.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі. Висота тону й тембр звуку.

Завдання скеровано на перевірку знання і розуміння характеристик звукових хвиль, а також уміння їх аналізувати.

Звуки різної частоти ми сприймаємо як звуки різного тону: що більшою є частота звуку, то вищий його тон і навпаки. Наприклад, у комара високий тон дзижчання, а у джмеля ‒ низький тон гудіння.

Хвиля (зокрема, звукова хвиля) ‒ це поширення коливань. Тому фізичні величини, які характеризують коливання (частота, період, амплітуда), також характеризують і хвилю.

Частота коливань \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) ‒ кількість \(N\) коливань за одиницю часу \(t:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac NT. $$

Середня кількість \(N\) помахів крил комах дана в умові з розрахунку на подолання відстані \(1\ \text{м}.\) А час можна визначити, узявши відстань \(l=1\ \text{м}\) і поділивши на середню швидкість руху \(v\) відповідної комахи:

\begin{gather*} t=\frac lv,\\[6pt] t_\text{бджоли}=\frac{1\ \text{м}}{15\ \text{м/c}}=\frac{1}{15}\ \text{c},\\[6pt] t_\text{оси}=\frac{1\ \text{м}}{14\ \text{м/c}}=\frac{1}{14}\ \text{c},\\[6pt] t_\text{мухи}=\frac{1\ \text{м}}{10\ \text{м/c}}=\frac{1}{10}\ \text{c},\\[6pt] t_\text{джмеля}=\frac{1\ \text{м}}{7\ \text{м/c}}=\frac{1}{7}\ \text{c}. \end{gather*}

Підставмо визначений для кожної комахи час у формулу для частоти:

\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{бджоли}=\frac{28\cdot 15}{1} \text{c}^{-1}=420\ \text{Гц},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{оси}=\frac{32\cdot 14}{1} \text{c}^{-1}=448\ \text{Гц},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{мухи}=\frac{33\cdot 10}{1} \text{c}^{-1}=330\ \text{Гц},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{джмеля}=\frac{32\cdot 7}{1} \text{c}^{-1}=224\ \text{Гц}. \end{gather*}

Порівняймо частоту помахів крил цих комах. Найбільшою є частота помахів в оси, тож звук її польоту буде видаватися людині найвищим.

Відповідь: Б.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Шкала електромагнітних хвиль.

Завдання скеровано на перевірку знання і розуміння видів електромагнітного випромінювання.

\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\textbf{-випромінювання}\) ‒ це позитивно заряджені важкі частинки (ядра атомів Гелію).
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\textbf{-випромінювання}:\) негативно заряджені легкі частинки (швидкі електрони).
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\textbf{-випромінювання}\) ‒ високочастотні електромагнітні хвилі довжиною менш ніж \(0,05\ \text{нм}.\)

Рентгенівське випромінювання ‒ це електромагнітні хвилі довжиною від \(0,001\ \text{нм}\) до \(100\ \text{нм}.\)

Отже, правильним варіантом відповіді буде рядок, у якому зазначене рентгенівське й \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\text{-випромінювання}.\)

Відповідь: Г.

Коментар

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси та енергії.

Завдання скеровано на перевірку знання і розуміння взаємозв’язку маси та енергії як наслідку постулатів спеціальної теорії відносності.

Будь-яке тіло (будь-яка частинка), що має масу \(m,\) несе із собою запас енергії \(E.\) Навіть якщо швидкість руху \(v\) тіла (частинки) зменшується до нуля, то згідно з формулою залежності енергії тіла від швидкості його руху $$ E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}} $$ тіло все одно має енергію: $$ E=mc^2, $$ де \(c\) ‒ швидкість світла у вакуумі.

Цю енергію називають енергією спокою.

Зміна енергії \(\Delta E\) тіла прямо пропорційна зміні його маси \(\Delta m:\) $$ \Delta E=\Delta mc^2. $$

Передавання нерухомому тілу енергії завжди супроводжується збільшенням його маси, а виділення тілом енергії супроводжується зменшенням його маси. Наприклад, якщо тіло нагрівають, його маса збільшується, а коли охолоджують, його маса зменшується.

Також енергія може змінюватися, коли тіло (частинка) рухається зі швидкістю, яка набагато менша, ніж швидкість світла \((v\lt\lt c).\) Тоді формулу залежності енергії тіла від швидкості його руху можна записати так: $$ E=mc^2+\frac{mv^2}{2}, $$ де \(mc^2\) ‒ енергія спокою; \(\frac{mv^2}{2}\) ‒ кінетична енергія (додаткова енергія, яка виникає внаслідок руху тіла (частинки)). Або ця додаткова енергія може бути за рахунок енергії пружно деформованого тіла, або за рахунок потенціальної енергії піднятого на певну висоту тіла.

Щодо праски, м’яча і пружини ‒ в усіх цих випадках енергія тіл збільшуватиметься через умови, що зазначені вище. А отже, і маса тіл збільшуватиметься.

А коли охолоджуватиметься конфорка електроплити, то зі зниженням температури зменшуватиметься внутрішня енергія конфорки, а тому зменшуватиметься і її маса.

Відповідь: A.

Коментар

Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерна модель атома.

Завдання скеровано на перевірку знання і розуміння будови ядра атома й сучасної моделі атома загалом.

Сучасне уявлення про будову атома ґрунтується на ядерній моделі атома, запропонованій Резерфордом і підтриманій Нільсом Бором. Кожний електрон усередині атома найімовірніше можна виявити в певній області навколо ядра; форма такої області визначається енергією електрона.

Атомне ядро складається із частинок двох видів: протонів, які мають позитивний електричний заряд, і нейтронів, які не мають заряду. Атом є електрично нейтральним: сумарний заряд протонів у ядрі дорівнює сумарному заряду електронів, що розташовані навколо ядра. Оскільки заряд протона за модулем дорівнює заряду електрона, то зрозуміло, що в атомі кількість протонів дорівнює кількості електронів.

Порядковий номер елемента в періодичній системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому або протонному числу). Отже, в ядрі атома Урану міститься \(92\) протони, а навколо ядра – \(92\) електрони. Разом елементарних заряджених частинок у нейтральному атомі Урану буде $$ 92+92=184. $$

Відповідь: Б.

Коментар

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.

Завдання скеровано на перевірку знання і розуміння понять кінетичної і потенціальної енергії, а також повної механічної енергії, уміння визначати характер змін енергії в різних ситуаціях.

Кінетична енергія ‒ це фізична величина, яка характеризує механічний стан рухомого тіла (швидкість тіла не дорівнює нулю): $$ E_k=\frac{mv^2}{2}. $$

Потенціальна енергія ‒ це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою: $$ E_p=mgh. $$

Повна механічна енергія системи тіл ‒ це сума кінетичної і потенціальної енергій системи.

А Людина стоїть у ліфті, що саме рушає з першого поверху на сьомий.

Якщо ліфт рушає, то він прискорюється, тож швидкість людини в ліфті також збільшуватиметься, відповідно зростатиме кінетична енергія. Якщо за нульовий рівень прийняти підлогу першого поверху, то відстань між людиною в рухомому ліфті й першим поверхом збільшуватиметься, унаслідок цього зростатиме потенціальна енергія людини. Повна механічна енергія збільшиться (4).

Б Парашутист відразу після стрибка рухається вниз, ще не відкривши парашут.

Потенціальна енергія парашутиста відносно землі зменшуватиметься, оскільки висота зменшуватиметься. А без парашута він летітиме з прискоренням і набиратиме швидкість, тому кінетична енергія збільшуватиметься. Повна механічна енергія змінюватися не буде (якщо знехтувати втратами).

Немає відповідного варіанту серед \(1‒4.\)

В Людина стоїть на ескалаторі, що піднімається.

Ескалатор їде із сталою швидкістю, тому кінетична енергія людини не змінюватиметься. Від основи ескалатора людина віддалятиметься, тобто її потенціальна енергія зростатиме. Отже, повна механічна енергія людини збільшуватиметься (1).

Г Спортсмен розбігається перед стрибком у довжину.

Спортсмен збільшує свою швидкість, тому зростатиме кінетична енергія. Потенціальна енергія не зміниться, тому що не зміниться її висота відносно бігової доріжки. А повна механічна енергія збільшуватиметься за рахунок кінетичної (2).

Д Після спуску зі снігової гірки хлопчик на санчатах їде горизонтальною поверхнею.

Через силу тертя ковзання швидкість руху хлопчика зменшуватиметься, тому кінетична енергія також зменшуватиметься. Потенціальна енергія хлопчика зменшиться до нуля відносно підніжжя гірки. Повна механічна енергія зменшуватиметься (3).

Відповідь: 1В, 2Г, 3Д, 4А.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Зміщення, амплітуда, період, частота і фаза гармонічних коливань.

Завдання скеровано на перевірку знання і розуміння характеристик механічних коливань і їхнього фізичного змісту.

1. Найбільша відстань, на яку відхиляється тіло від положення рівноваги, ‒ це амплітуда коливань (А).

2. Найменший проміжок часу, через який коливання повторюються, ‒ це період коливань (Г).

3. Величина, що характеризує стан коливальної системи в певний момент часу, ‒ це фаза коливань (Д).

4. Кількість коливань за одиницю часу ‒ це частота коливань (Б).

Відповідь: 1А, 2Г, 3Д, 4Б.

Коментар

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Лінійна і кутова швидкості.

Завдання скеровано на перевірку знання і розуміння характеристики рівномірного руху по колу ‒ лінійної швидкості.

За час одного оберту (\(T=\frac tN,\) де \(T\) ‒ період обертання, \(N\) ‒ кількість обертів за час \(t\)) тіло долає відстань \(l,\) що дорівнює довжині кола радіуса \(r:\) $$ l=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r. $$

Оскільки \(v=\frac lt,\) дістанемо формулу для визначення лінійної швидкості:

Відповідь: 62,8.

Коментар

ТЕМА: Механіка. Основи динаміки. Рух тіл під дією однієї або кількох сил.

Завдання скеровано на перевірку знання і розуміння кінематичних характеристик руху, а також на застосування другого закону Ньютона.

Щоб забезпечити мінімальний час \(t\) переміщення \(s\) вантажу, він повинен рухатися з прискоренням \(a:\) $$ s=v_0t+\frac{at^2}{2}=\frac{at^2}{2}, $$ де \(v_0=0\) ‒ початкова швидкість руху вантажу дорівнює нулю за умовою.

Виразімо час: \begin{gather*} t=\sqrt{\frac{2s}{a}}. \end{gather*}

Щоб час був мінімальним, прискорення повинно бути максимальним. Відстань, яку тіло повинно пройти, задано в умові (вона не змінюється): $$ t_\text{min}=\sqrt{\frac{2s}{a_\text{max}}}. $$

Визначмо \(a_\text{max}.\) За другим законом Ньютона $$ ma_\text{max}=F_\text{тяги}-F_\text{тертя}, $$ де \(ma_\text{max}\) ‒ рівнодійна сил, що діють на вантаж, \(m\) ‒ маса вантажу, \(F_\text{тяги}=30\ \text{Н}\) ‒ проєкція сили, обернена до максимальної сили натягу мотузки, \(F_\text{тертя}\) ‒ ця проєкція сили, що напрямлена протилежно до напрямку руху й за модулем дорівнює силі натягу, що виникає в мотузці під час рівномірного руху.

\begin{gather*} a_\text{max}=\frac{F_\text{тяги}-F_\text{тертя}}{m},\\[6pt] a_\text{max}=\frac{30\ \text{Н}-20\ \text{Н}}{100\ \text{кг}}=0,1\ \text{м/с}^2. \end{gather*}

Підставмо значення прискорення у формулу для часу й обчислімо його:

$$ t_\text{min}=\sqrt{\frac{2\cdot 5\ \text{м}}{0,1\ \text{м/с}^2}}=\sqrt{100}\ \text{с}=10\ \text{с}. $$

Відповідь: 10.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та вимірювання її.

Завдання скеровано на перевірку знання і розуміння поняття відносної вологості водяної пари й уміння користуватися таблицями.

Відносна вологість \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) ‒ фізична величина, яка показує, наскільки водяна пара близька до насичення. Вона дорівнює поданому у відсотках відношенню абсолютної вологості \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_a\) до густини насиченої водяної пари \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{н.п.}\) за певної температури: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_a}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{н.п.}}\cdot 100\ \text{%}. $$

Густина водяної пари прямо пропорційна її парціальному тиску \(p_a,\) тому відносну вологість повітря можна визначити зі співвідношення $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{p_a}{p_{н.п.}}\cdot 100\ \text{%}. $$

Визначмо парціальний тиск водяної пари, узявши до уваги, що згідно з умовою вдень за температури \(29\ ^\circ\mathrm{C}\) відносна вологість повітря становила \(55\ \text{%}.\) Відповідно за таблицею в умові тиск насиченої пари за такої температури становить \(p_{н.п.}=4\ \text{кПа}=4\cdot 10^3\ \text{Па}.\) Тобто

За умовою ввечері за цього ж тиску \(p_a\) почала утворюватися роса. Тобто цей тиск тепер став тиском насичення водяної пари за вечірньої температури. Визначмо її за таблицею ‒ тиску \(2,2\ \text{кПа}\) відповідає температура \(19\ ^\circ\mathrm{С}.\)

Відповідь: 19.

Коментар

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.

Завдання скеровано на перевірку знання і розуміння сили Ампера й уміння застосовувати другий закон Ньютона до комбінованих задач.

Магнітне поле діє на провідник зі струмом із силою Ампера. Якщо провідник прямолінійний, а магнітне поле, у якому він перебуває, однорідне, то модуль сили Ампера визначають за формулою $$ F_\text{A}=BIl\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(B\) ‒ магнітна індукція поля, у якому перебуває провідник; \(I\) ‒ сила струму в провіднику; \(l\) ‒ довжина активної частини провідника; \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) ‒ кут між вектором магнітної індукції і напрямком струму.

За умовою кут між лініями магнітної індукції і провідником дорівнює \(90^\circ.\) Отже, \(\sin90^\circ=0.\)

Якщо сили натягу підвісних дротів збільшилися, то сила Ампера напрямлена вертикально вниз, куди весь час була напрямлена сила тяжіння, що діє на провідник.

Запишімо в проєкціях другий закон Ньютона для провідника: $$ 2T=mg+F_A, $$ де \(T\) ‒ сила натягу одного дроту, \(m\) ‒ маса провідника, \(g\) ‒ прискорення вільного падіння.

Підставмо дані з умови і обчислимо силу натягу кожного з дротів:

Відповідь: 0,25.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.

Завдання скеровано на перевірку знання і розуміння законів відбивання, а також вміння робити побудови за допомогою плоского дзеркала.

За законом відбивання промінь повинен був відбитися під таким самим кутом, що й упав. Але треба, щоб відбитий промінь відбився вертикально вгору. Це означає: якщо поділимо бісектрисою кут падіння навпіл, то ця бісектриса має бути перпендикуляром до дзеркала (див. рисунок).

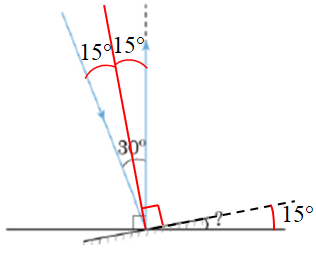
За побудовою бачимо, що перпендикуляр до площини дзеркала повернутий від початкового перпендикуляра до площини падіння променя на \(15^\circ,\) отже, і площина, пов’язана з перпендикуляром, повернеться на \(15^\circ.\) Тому плоске дзеркало треба розмістити під кутом \(15^\circ\) до горизонту.

Відповідь: 15.

Коментар

ТЕМА: Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.

Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.

Скористаймося основним законом радіоактивного розпаду: $$ N=N_0\cdot 2^{-\frac tT}, $$ де \(N\) ‒ кількість ядер радіонукліда, що залишились у зразку через час \(t;\) \(N_0\) ‒ початкова кількість ядер; \(T\) ‒ період піврозпаду; \(t\) ‒ час розпаду.

За умовою \begin{gather*} t_1=t_2=t, \end{gather*} для першого нукліда: \(N_{01}\) ‒ початкова кількість ядер; залишиться \(N_1=\frac{N_{01}}{8};\)
для другого нукліда: \(N_{02}\) ‒ початкова кількість ядер; залишиться \(N_2=\frac{N_{02}}{4}.\)

Запишімо закон піврозпаду для кожного нукліда й розв’яжемо систему рівнянь:

Відповідь: 1,5.