НМТ онлайн 2025 року з фізики – 1 сесія
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку знання і розуміння кінематичного рівняння для координати, що описує прямолінійний рівноприскорений рух.
Запишімо рівняння для прямолінійного рівноприскореного руху тіла в загальному вигляді: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x\) ‒ кінцева координата тіла, \(x_0\) ‒ початкова координата тіла, \(v_0\) ‒ модуль початкової швидкості руху тіла, \(a\) ‒ модуль прискорення руху тіла, \(t\) ‒ час руху тіла.
Підставмо всі значення відповідних величин з умови в це рівняння:
\begin{gather*} x=10+2\mathord{,}5t+\frac{5t^2}{2},\\[6pt] x=10+2\mathord{,}5t+2\mathord{,}5t^2. \end{gather*}Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Вага тіла. Невагомість.
Завдання скеровано на перевірку знання і розуміння стану невагомості.
Стан тіла, за якого вага тіла дорівнює нулю, називають станом невагомості.
У стані невагомості на тіло діє лише сила тяжіння (тіло вільно падає), і навпаки: якщо тіло рухається тільки під дією сили тяжіння, воно перебуває в стані невагомості.
Проаналізуймо стан запропонованих в умові рухомих об’єктів.
Якщо діти підстрибнули, відірвалися від землі, то вони не тиснуть на опору (на землю), а отже, їхня вага дорівнюватиме нулю. Цієї миті діти перебувають у стані невагомості. Також уважатимемо, що на дітей діє тільки сила тяжіння, опором повітря можна в цій ситуації знехтувати, настільки він незначний.
Підлітки у ліфті тиснуть на опору ‒ на підлогу ліфта, отже, вага не дорівнює нулю. Цей стан не є станом невагомості. Це правильна відповідь.
За умовою завдання повітря з трубки Ньютона відкачано. Падіння тіл у безповітряному просторі називають вільним, тобто це падіння лише під дією сили тяжіння. Отже, тіла у трубці ‒ у стані невагомості.
На космонавта у відкритому космосі, як зображено на фото, діє сила тяжіння, але ні опори, ні підвісу немає, тому вага космонавта дорівнює нулю ‒ стан невагомості.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку знання і розуміння закону збереження механічної енергії, а також уміння застосовувати його в конкретних ситуаціях.
Суму кінетичної \(E_k\) і потенціальної \(E_p\) енергій системи називають повною механічною енергією \(E\) системи тіл: $$ E=E_p+E_k. $$
У замкненій системі тіл, які взаємодіють лише консервативними силами, повна механічна енергія залишається незмінною (зберігається):
\begin{gather*} E_{p0}+E_{k0}=E_p+E_k. \end{gather*}Відповідно до умови завдання запишімо вирази, які визначають кінетичну і потенціальну енергії до і після маневру.
Отже, повна механічна енергія літака на початку становить \(E_0.\) Якщо кінетична енергія дорівнює потенціальній, то $$ E_{k0}=E_{p0}=\frac{E_0}{2}. $$
Умова, що потенціальна енергія літака на поверхні Землі дорівнює нулю, означає, що Землю вибрано як нульовий рівень.
Після маневру швидкість \(v\) літака за модулем зменшилася вдвічі, тоді кінетична енергія \(E_k\) зменшиться вчетверо:
Висота ж літака над поверхнею Землі збільшилася вдвічі, тож і потенціальна енергія \(E_p\) збільшиться вдвічі:
Тоді повна енергія \(E\) літака після маневру:
$$ E=E_p+E_k=E_0+\frac{E_0}{8}=\frac 98E_0. $$Закон збереження повної механічної енергії передбачає перетворення кінетичної енергії на потенціальну й навпаки. Однак досвід доводить, що водночас повна механічна енергія не зберігається.
Річ у тім, що закон збереження повної механічної енергії виконується тільки тоді, коли в системі немає тертя. Однак у природі не існує рухів без тертя.
Енергія нікуди не зникає і нізвідки не з’являється: вона лише перетворюється з одного виду на інший, передається від одного тіла до іншого.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Середня квадратична швидкість теплового руху молекул. Ізопроцеси в газах.
Завдання скеровано на перевірку знання і розуміння ізопроцесів у газі, а також уміння визначати зміну характеристик ідеального газу під час переходу його з одного стану в інший.
Відповідно до графіка абсолютна температура \(T\) ідеального газу знижується, а тиск \(p\) залишається сталим, отже, з газом відбувається ізобарний процес:
Як випливає із закону Ґей-Люссака, за незмінного тиску об’єм \(V\) газу певної маси прямо пропорційний його температурі: $$ V=\mathrm{const}\cdot T. $$
Отже, якщо за умовою абсолютна температура газу знизиться, то і його об’єм зменшиться.
Щодо середньої квадратичної швидкості теплового руху молекул.
Квадратний корінь із середнього квадрата швидкості називають середньою квадратичною швидкістю руху молекул \((\overline{v}_\text{кв}):\) $$ \overline{v}_\text{кв}=\sqrt{\overline{v^2}}. $$ (Середній квадрат швидкості \((\overline{v^2}):\) $$ \overline{v^2}=\frac{v_1^1+v_2^2+\text{...}+v_N^2}{N}, $$ де \(N\) ‒ кількість молекул; \(v_1\), \(v_2\), ... \(v_N\) ‒ швидкості руху окремих молекул.)
Середній квадрат швидкості \(\overline{v^2}\) можна визначити з формули для середньої кінетичної енергії \(\overline{E}_k\) поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)): $$ \overline{E}_k=\frac{m_0\overline{v^2}}{2}. $$
Залежність середньої кінетичної енергії поступального руху молекул ідеального газу від абсолютної температури \(T\) визначмо за формулою: $$ \overline{E}_k=\frac 32kT, $$ де \(k\) ‒ стала Больцмана.
Прирівняймо обидва вирази для визначення середньої кінетичної енергії поступального руху молекул ідеального газу: $$ \frac{m_0\overline{v^2}}{2}=\frac 32kT, $$ звідки $$ \overline{v^2}=\frac{3kT}{m_0}, $$ або $$ \overline{v}_\text{кв}=\sqrt{\overline{v^2}}=\sqrt{\frac{3kT}{m_0}}. $$
Проаналізуймо зміну \(\overline{v}_\text{кв}\) під час переходу газу зі стану \(1\) у стан \(2:\)
середня квадратична швидкість \(\overline{v}_\text{кв}\) руху молекул газу прямо пропорційна його абсолютній температурі \(T\), за графіком з умови температура знижується, отже, і середня квадратична швидкість теж зменшується.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Закон збереження енергії в теплових процесах (перший закон термодинаміки). Адіабатний процес.
Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки й уміння застосувати його до адіабатного процесу.
Перший закон (начало) термодинаміки: кількість теплоти \(Q\), передана системі, йде на зміну внутрішньої енергії \(\Delta U\) системи й на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$
Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. В адіабатному процесі кількість теплоти \(Q\), передана системі, дорівнює нулю ‒ теплообміну немає (можна відкинути варіанти відповіді Б й В), тому перший закон термодинаміки має вигляд: $$ \Delta U+A=0. $$
Під час адіабатного стискання газ виконує від’ємну роботу (додатну роботу виконуватимуть над газом), водночас внутрішня енергія збільшуватиметься, температура газу зростатиме: $$ A=-\Delta U=-50\ \text{Дж}. $$
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля при переміщенні заряду.
Завдання скеровано на перевірку знання і розуміння поняття роботи електричного поля при переміщенні заряду.
За означенням робота \(A\) дорівнює добутку модуля сили \(F\), модуля переміщення \(s\) і косинуса кута \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) між вектором сили й вектором переміщення: $$ A=Fs\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. $$
Поле однорідне, тому сила \(\overrightarrow{F}\) є незмінною, її модуль дорівнює: $$ F=qE, $$ a \(s\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=x_2-x_1\) є проекцією вектора переміщення на напрямок силових ліній поля (див. рисунок).
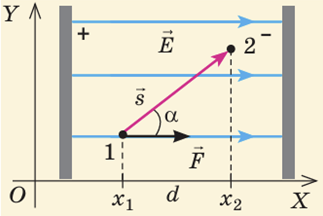
Тоді робота сил однорідного електростатичного поля напруженістю \(\overrightarrow{E}\) під час переміщення електричного заряду \(q\) із точки \(1\) у точку \(2\) \((A_{1\rightarrow 2})\) дорівнюватиме: $$ A_{1\rightarrow 2}=qE(x_2-x_1). $$
Якби заряд переміщувався не з точки \(1\) у точку \(2\), а навпаки, то знак роботи змінився б на протилежний, тобто робота виконувалась би проти сил поля.
За умовою електричне поле створено негативним зарядом, отже, силові лінії будуть направлені до цього заряду (рис. 1). Відповідно й вектор напруженості теж буде направлений до джерела поля (рис. 2), тому що за напрямок вектора напруженості в даній точці \(C\) електричного поля беруть напрямок сили, яка діяла б на пробний позитивний заряд, якби він був поміщений у цю точку поля.
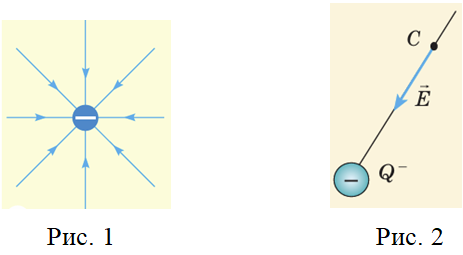
Якщо позитивний заряд \(q\) рухатиметься по дугах \(AB\) і \(CD\), то електричне поле не виконуватиме роботу під час обертання заряду по колу навколо джерела поля за умови, що це обертання відбувається зі сталою швидкістю і в електростатичному полі.
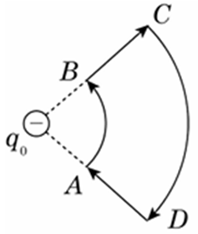
Це пов’язано з тим, що сила поля перпендикулярна до напрямку переміщення (і робота поля залежить лише від різниці потенціалів між початковою і кінцевою точками): $$ \cos 90^\circ = 0\Rightarrow A=Fs\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=0. $$
Якщо ж заряд \(q\) переміщати вздовж ділянки \(DA\), то робота буде додатна. А якщо заряд \(q\) перемістити вздовж ділянки \(BC\), то робота буде від’ємна, оскільки буде виконана проти сил поля.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і розуміння законів постійного струму, і вміння визначати залежність фізичних величин, що характеризують електричний струм.
Потужність струму \(P\) ‒ фізична величина, яка чисельно дорівнює роботі струму за одиницю часу: $$ P=\frac At, $$ де \(A\) ‒ робота, виконана струмом за час \(t.\)
Узявши до уваги, що \begin{gather*} A=UIt, \end{gather*} маємо $$ P=UI, $$ де \(U\) ‒ напруга на ділянці кола, на якій визначають потужність струму; \(I\) ‒ сила струму в ділянці.
Зауважмо, що за умовою напруга стала.
А якщо вкоротити спіраль (тобто меншою стане довжина \(l\) спіралі, при тому, що питомий опір \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) і площа \(S\) поперечного перерізу залишаться тими самими) електронагрівального пристрою, то зменшиться її електричний опір \(R\): $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS. $$
Згідно із законом Ома $$ I=\frac UR, $$ тоді $$ P=\frac{U^2}{R}. $$
Висновок: якщо напруга залишається сталою, а опір зменшується (залежність обернена \(P\sim \frac 1R\)), то потужність нагрівального пристрою збільшиться.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Досліди Фарадея. Явище електромагнітної індукції. Правило Ленца.
Завдання скеровано на перевірку знання і розуміння дослідів Фарадея, а також уміння застосовувати правило Ленца для визначення напрямку індукційного струму.
Пригадаймо висновок, який зробив Майкл Фарадей на основі своїх дослідів. Ці досліди доводили, що за допомогою магнітного поля можна отримати електричний струм: у замкненому провідному контурі виникає електричний струм, якщо кількість ліній магнітної індукції, що пронизують поверхню, обмежену контуром, змінюється.
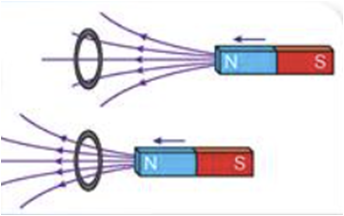
Це явище назвали електромагнітною індукцією, а електричний струм, який при цьому виникає, ‒ індукційним (наведеним) струмом.
Якщо змінювати магнітне поле, що пронизує котушку (наприклад, наближати або віддаляти магніт, як сказано в умові завдання), то в котушці виникає індукційний струм. Унаслідок цього котушка сама стає магнітом.
Як свідчать досліди, якщо магніт наближати до котушки (за умовою північним полюсом), то кількість ліній магнітної індукції, що пронизують котушку, збільшується (магнітне поле всередині котушки посилюється), і в ній виникає індукційний струм такого напрямку, що котушка буде обернена до магніту однойменним полюсом \(N\) (див. рисунок 1). Котушка в цій ситуації відштовхуватиметься від магніту. Іншими словами, за правилом Ленца в котушці повинен виникнути індукційний струм такого напрямку, щоб власним магнітним полем протидіяти зростанню зовнішнього магнітного потоку. Для цього треба виштовхнути магніт з котушки. Це означає, що з того боку котушки, який повернуто до магніту, з’являється однойменний полюс \(Ν.\)
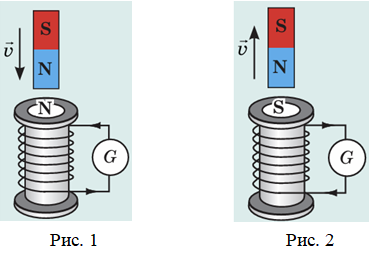
Якщо ж магніт віддаляти від котушки, то кількість ліній магнітної індукції, що пронизують котушку, зменшується, і в котушці виникає індукційний струм такого напрямку, що котушка буде обернена до магніту різнойменним полюсом \(S\) (див. рисунок 2). У цій ситуації котушка притягуватиметься до магніту. Або ж за правилом Ленца в котушці повинен виникнути індукційний струм такого напрямку, щоб власним магнітним полем підтримувати спадання зовнішнього магнітного потоку від магніту, що віддаляється. Для цього треба притягнути магніт до котушки. Це означає, що з того боку котушки, який повернуто до магніту, з’являється різнойменний полюс \(S.\)
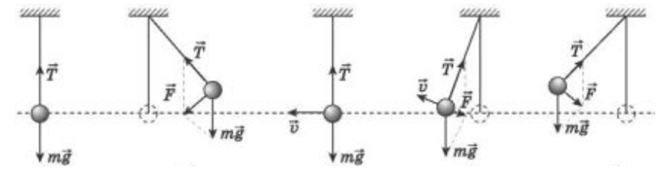
Знаючи полюси котушки та скориставшись правилом правої руки (див. рисунок),
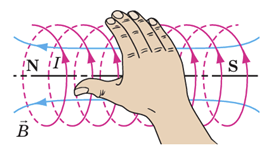
можна визначити напрямок індукційного струму (на обох рисунках 1 і 2 напрямок струму позначено стрілками на обмотках котушок, з’єднаних із гальванометром \((G)\)).
Отже, у першій ситуації (унаслідок наближення магніту) котушка й магніт відштовхуватимуться, а в другій (унаслідок віддалення магніту) ‒ притягуватимуться.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку знання і розуміння залежності періоду коливань нитяного маятника від його параметрів, і вміння визначати їх.
Запишімо формулу для обчислення періоду \(T\) коливань маятника \(M:\) $$ T_M=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{l_M}{g}}, $$ де \(l_M\) ‒ довжина маятника \(M\) (виразімо її в одиничних відрізках \(l_0\) ‒ довжина сторони однієї клітинки ‒ \(l_M=8l_0\)), \(g\) ‒ прискорення вільного падіння. Отже,
\begin{gather*} T_M=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{8l_0}{g}},\\[6pt] 1\mathord{,}6=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{8l_0}{g}}. \end{gather*}З умови нам відомий період коливань іншого маятника – \(T=1\mathord{,}2\ \text{с}.\) Запишімо формулу для нього: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac lg}. $$
Його довжина \(l\) в одиничних відрізках кількістю \(N\) становитиме: $$ l=Nl_0, $$ тоді $$ 1\mathord{,}2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{Nl_0}{g}}. $$
Поділімо ліві і праві частини цих рівностей:
\begin{gather*} \frac{1\mathord{,}6}{1\mathord{,}2}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{8l_0}{g}}:2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac{Nl_0}{g}},\\[6pt] \frac 43=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{8l_0}}{\sqrt{g}}\cdot \frac{\sqrt{g}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{Nl_0}},\\[6pt] \frac 43=\frac{\sqrt{8}}{\sqrt{N}},\\[6pt] \frac{16}{9}=\frac 8N,\\[6pt] N=\frac{9\cdot 8}{16}=4\mathord{,}5. \end{gather*}Отже, довжина шуканого маятника \(4\mathord{,}5\) одиничних відрізка, тобто \(4\mathord{,}5\) клітинки ‒ це маятник \(2.\)
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі.
Завдання скеровано на перевірку знання і розуміння властивостей механічних і електромагнітних хвиль.
Звукові (акустичні) хвилі ‒ це механічні хвилі з частотами від \(20\ \text{Гц}\) до \(20\ \text{кГц}.\)
Електромагнітні хвилі ‒ це процес поширення в просторі електричних і магнітних полів, що періодично змінюються. Їхній діапазон частот від \(3\ \text{кГц}\) і понад \(6\cdot 10^{19}\ \text{Гц}.\)
Інтерференція, здатність відбиватися від перешкоди, огинання хвилями перешкод (дифракція) ‒ усі ці явища характерні і для механічних, і для електромагнітних хвиль.
Інтерференція ‒ явище накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.
Дифракція ‒ явище огинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики.
Відбивання хвиль від перешкоди ‒ це явище, коли хвиля, досягнувши межі між двома середовищами або перешкоди, повертається назад, не поширюючись далі через цю межу. Це явище, яке пояснює утворення луни (відбивання звуку) та роботу радарів, є властивістю всіх типів хвиль (звукових, світлових, радіохвиль).
Щодо поширення хвиль: механічні хвилі потребують матеріального середовища для поширення, тоді як електромагнітні хвилі можуть поширюватися у вакуумі. Це пов’язано з тим, що механічні хвилі є коливаннями частинок у середовищі (наприклад, звукові хвилі), а електромагнітні хвилі ‒ це коливання електричного та магнітного полів, що можуть існувати без середовища.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).
Завдання скеровано на перевірку знання і розуміння залежності енергії фотона від частоти й довжини хвилі.
Енергія \(E\) фотона прямо пропорційна частоті \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) електромагнітного випромінювання, квантом якого і є цей фотон (\(h\) ‒ стала Планка): $$ E=h\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}. $$
Скористаймося формулою зв’язку довжини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\), частоти \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) та швидкості \(c\) поширення хвилі ‒ формулою хвилі:
\begin{gather*} c=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}},\\[6pt] E=h\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac{hc}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}. \end{gather*}За умовою треба визначити колір променів (визначмо це за довжинами хвиль відповідно до таблиці), щоб їхні фотони мали енергію більшу, ніж фотони променів блакитного кольору. Тож цій умові відповідатимуть промені з коротшою довжиною хвилі ‒ оскільки \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) в знаменнику, то що вона менша, то енергія буде більша. Отже, варіанти відповіді В і Г неправильні. Перевірмо варіанти відповіді А і Б:
\begin{gather*} E_\text{блакитний}=\frac{hc}{485\ \text{нм}},\\[6pt] E_\text{шуканий}=1\mathord{,}1E_\text{блакитний}=\frac{hc}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}. \end{gather*}Поділімо ліві і праві частини цих рівностей:
\begin{gather*} \frac{E_\text{блакитний}}{1\mathord{,}1E_\text{блакитний}}=\frac{hc}{485\ \text{нм}}:\frac{hc}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}},\\[6pt] \frac{1}{1\mathord{,}1}=\frac{hc}{485\ \text{нм}}\cdot \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{hc},\\[6pt] \frac{1}{1\mathord{,}1}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{485\ \text{нм}},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac{485\ \text{нм}}{1\mathord{,}1}\approx 441\ \text{нм}. \end{gather*}Отримане значення довжини хвилі згідно з таблицею відповідає діапазону хвиль синього кольору.
Відповідь: Б.
Знайшли помилку? Пишіть на
Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку знання і розуміння будови атома і ядра атома.
Порядковий номер елемента в періодичній системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому числу). Зарядовим (протонним) числом називають кількість протонів у ядрі й позначають символом \(\mathrm{Z}.\)
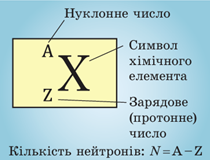
Запишімо рівняння ядерної реакції відповідно до умови:
$$ \mathrm{^{14}_{\ \ 7}N}+^{\ \ \ 0}_{-1}e\rightarrow \mathrm{X}+\ ^1_1p. $$Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Відповідно до закону збереження електричного заряду й закону збереження енергії-маси визначімо \(\mathrm{A}\) ‒ нуклонне (масове) й \(\mathrm{Z}\) ‒ протонне (зарядове) числа нукліда елемента \(\mathrm{X}:\)
\begin{gather*} \mathrm{A}=(14+0)-1=13,\\[7pt] \mathrm{Z}=(7+(-1))-1=5. \end{gather*}Отже, унаслідок такої реакції утворився нуклід \(\mathrm{^{13}_{\ \ 5}X}\) ‒ його порядковий номер у таблиці елементів \(5.\)
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку знання і розуміння сил в динаміці, а також уміння визначати їхню залежність від певних параметрів у кожній конкретній ситуації.
А ‒ 2. Коли тіло перебуває в стані спокою на похилій площині, то сила тертя спокою дорівнює за модулем проєкції сили тяжіння на вісь \(OX\), спрямованій уздовж площини, і зростає зі збільшенням кута нахилу, доки не досягне свого максимуму, і тоді сила тертя спокою стане силою тертя ковзання.
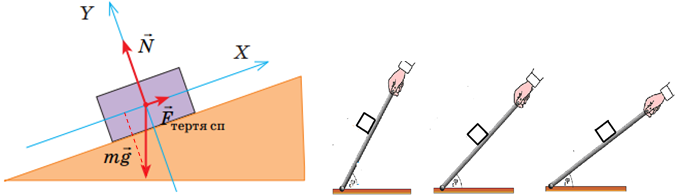
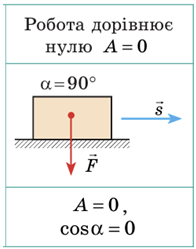
Б ‒ 1. Механічна робота (робота сили) \(A\) ‒ це фізична величина, яка характеризує зміну механічного стану тіла й дорівнює добутку модуля сили \(F\), модуля переміщення \(s\) і косинуса кута \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) між вектором сили та вектором переміщення: $$ A=Fs\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. $$
Оскільки вектор сили тяжіння завжди напрямлений вертикально вниз, а за умовою автомобіль рухається горизонтальною дорогою, то кут між вектором сили тяжіння і вектором переміщення дорівнює \(90^\circ\), отже, \(\cos 90^\circ=0\), а сила роботу не виконує: $$ A=0. $$
В ‒ 4. За законом всесвітнього тяжіння будь-які два тіла притягуються одне до одного із силою \(F\), яка прямо пропорційна добутку мас \(m_1\) i \(m_2\) цих тіл і обернено пропорційна квадрату відстані \(r\) між ними: $$ F=G\frac{m_1m_2}{r^2}. $$
Відповідно до заданої в умові ситуації сили гравітаційної взаємодії між Сонцем і Землею не змінюватимуться (але й не дорівнюватимуть нулю).
Г ‒ 3. Сила пружності \(F_\text{пруж}\), яка діє з боку рейок на бокову поверхню коліс, коли швидкість \(v\) руху поїзда на повороті (\(R\) ‒ радіус повороту, \(a_\text{доц}\) ‒ доцентрове прискорення) стає меншою, зменшується. На повороті ця сила пружності надає поїзду доцентрового прискорення.
За другим законом Ньютона:
\begin{gather*} F_\text{пруж}=ma_\text{доц},\\[6pt] F_\text{пруж}=m\frac{v^2}{R}. \end{gather*}Отже, проаналізуємо цю рівність. Якщо поїзд скидає швидкість на повороті (\(v\) зменшується), то й сила пружності при незмінному радіусі повороту теж зменшуватиметься:
\begin{gather*} F_\text{пруж}\sim v^2. \end{gather*}Під час коливань нитяного маятника сила натягу його нитки весь час змінюється, досягаючи максимуму в нижній точці (найнижчій точці траєкторії) і мінімуму на крайніх точках (коли маятник зупиняється). У найнижчій точці сила натягу дорівнює сумі сили тяжіння та сили, що створює доцентрове прискорення. Сила натягу максимальна, оскільки вона повинна протидіяти силі тяжіння та забезпечувати доцентрове прискорення, яке спрямоване до центру кола (точки підвісу). У крайніх точках сила натягу мінімальна і дорівнює проекції силі тяжіння. У ці моменти швидкість маятника дорівнює нулю, тому немає сили, що створює доцентрове прискорення.
Відповідь: 1Б, 2А, 3Г, 4В.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах.
Завдання скеровано на перевірку знання і розуміння проходження процесів електричного струму в різних середовищах.
1 ‒ Б. Відразу після того як відбувся контакт двох напівпровідників із різними типами провідності, починається дифузія електронів і дірок. Електрони дифундують у напівпровідник \(p\text{-типу}\), і деякі з них рекомбінують із дірками; дірки «дифундують» у напівпровідник \(n\text{-типу}\), і деякі з них рекомбінують із вільними електронами. Тобто відбуваються процеси відновлення зв’язків (див. рисунок).
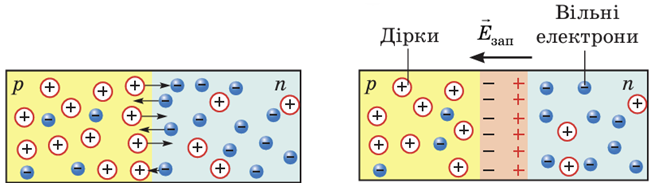
Унаслідок цих процесів:
1) у прилеглих до місця контакту ділянках напівпровідників зменшується концентрація вільних носіїв струму (\(n\text{-ділянка}\) втрачає вільні електрони, \(p\text{-ділянка}\) ‒ дірки), тому опір ділянки біля місця контакту істотно збільшується;
2) прилегла до місця контакту \(n\text{-ділянка}\) набуває позитивного заряду; прилегла до місця контакту \(p\text{-ділянка}\) набуває негативного заряду. Отже, навколо місця контакту формується подвійний запірний шар (\(p-n\) перехід).
Електронно-дірковий перехід (\(p-n\) перехід) ‒ це ділянка контакту двох напівпровідників із різними типами провідності ‒ дірковою (напівпровідник \(p\text{-типу}\)) та електронною (напівпровідник \(n\text{-типу}\)).
2 ‒ Г. Іскровий газовий розряд, який відбувається без дії зовнішнього йонізатора, називають самостійним газовим розрядом. Виникає він за атмосферного тиску та великої напруги між електродами. Має вигляд яскравих зигзагуватих смуг, що розгалужуються, триває лише кілька десятків мікросекунд і зазвичай супроводжується звуковими ефектами (потріскування, тріск, грім тощо). Використовують у запальних свічках бензинових двигунів, для обробки особливо міцних металів, для запобігання перенапрузі ліній електропередачі (іскрові розрядники). Приклад грандіозного іскрового розряду в природі ‒ блискавка.
3 ‒ А. У разі зниження температури деяких металів до температур, близьких до абсолютного нуля, їхній опір стрибком падає до нуля. Це явище називають надпровідністю.
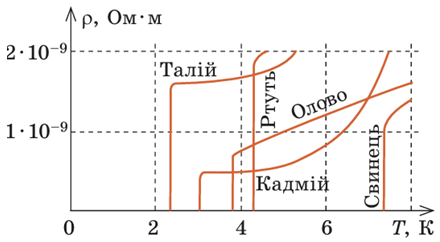
Якщо в замкненому провіднику, який перебуває в надпровідному стані, створити електричний струм, то струм існуватиме в провіднику без підтримки джерела необмежений час. Створення надпровідних ліній електропередачі дозволяє зекономити \(10–15\ \text{%}\) електроенергії. Труднощі широкого застосування надпровідників пов’язані з необхідністю охолодження матеріалів до низьких температур ‒ це досить дорого коштує. Зараз створено матеріали, які переходять у надпровідний стан за температури близько \(100\ \text{К}\ (–173\ ^\circ\mathrm{C})\) і нижче. Останній рекорд високотемпературної надпровідності був поставлений 2015 р.: за величезного тиску (\(1\) млн атм) сірководень \(\mathrm{H_2S}\) перевели в надпровідний стан за температури \(–70\ ^\circ\mathrm{C}.\)
4 ‒ Д. Гальванопластика ‒ виготовлення за допомогою електролізу точних копій рельєфних виробів. Наприклад, восковий зліпок, укритий тонким шаром графіту, є катодом, срібна пластинка ‒ анодом (див. рисунок).
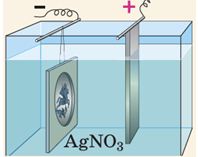
Метал нарощують на матриці (оригіналі) до потрібної товщини, а потім відокремлюють від неї, формуючи самостійний виріб, що точно відтворює форму оригіналу. Цей метод застосовують для створення складних виробів, які важко виготовити іншими способами, а також у ювелірній справі та для декоративних цілей.
Відповідь: 1Б, 2Г, 3А, 4Д.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку знання і розуміння поняття обертової частоти, і вміння її визначати.
Обертова частота \(n\) ‒ фізична величина, яка чисельно дорівнює кількості \(N\) обертів за одиницю часу \(t:\) $$ n=\frac Nt. $$
Одиниця обертової частоти в SІ ‒ оберт за секунду: $$ [n]=1\frac{\text{об}}{\text{с}}=\text{с}^{-1}. $$
Обчислимо частоту обертання барабана пральної машини:
\begin{gather*} n=\frac{900\ \text{об}}{60\ \text{с}}=15\frac{\text{об}}{\text{с}}=15\ \text{с}^{-1}. \end{gather*}Відповідь: \(15.\)
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин і газів. Гідростатичний тиск. Атмосферний тиск.
Завдання скеровано на перевірку знання і розуміння атмосферного й гідростатичного тисків і їхніх властивостей.
На повітря під ртуттю тисне повітря (позначмо цей тиск як \(p_\text{атм}\)), що заходить через відкритий верхній кінець, і стовпчик ртуті, гідростатичний тиск якого позначмо \(p_\text{гідр}.\) Тиск повітря під ртуттю позначмо \(p_\text{п1}.\) Прирівняймо ці тиски: $$ p_\text{п1}=p_\text{атм}+p_\text{гідр}. $$
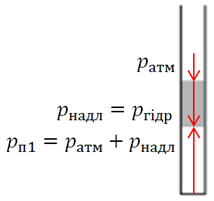
Повітря під ртуттю за умовою має надлишковий тиск \(p_\text{надл}.\) Можемо зробити висновок, що надлишковий тиск повітря під ртуттю дорівнюватиме гідростатичному тиску стовпчика ртуті: \begin{gather*} p_\text{надл}=p_\text{гідр}=20\ \text{кПа}. \end{gather*}
Обчислімо тиск повітря під ртуттю: $$ p_\text{п1}=100\ \text{кПа}+20\ \text{кПа}=120\ \text{кПа}. $$
Коли ж повернути трубку у вертикальній площині на \(180^\circ\), тоді атмосферний тиск повітря, що заходить через відкритий нижній кінець трубки, буде витримувати гідростатичний тиск стовпчика ртуті і тиск повітря, що міститься у заблокованій ртуттю частині трубки (див. рисунок).
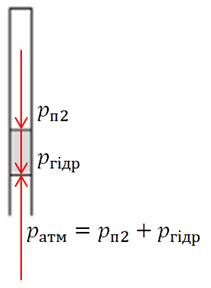
Отже, визначимо тиск повітря в трубці після її перевертання:
Відповідь: \(80.\)
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Модуль Юнга.
Завдання скеровано на перевірку знання і розуміння механічних властивостей твердих тіл і вміння визначати характеристики деформацій твердих тіл.
Пригадаймо діаграму напруг ‒ графік залежності механічної напруги \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}\) від відносного видовження \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\) зразка (див. рисунок).
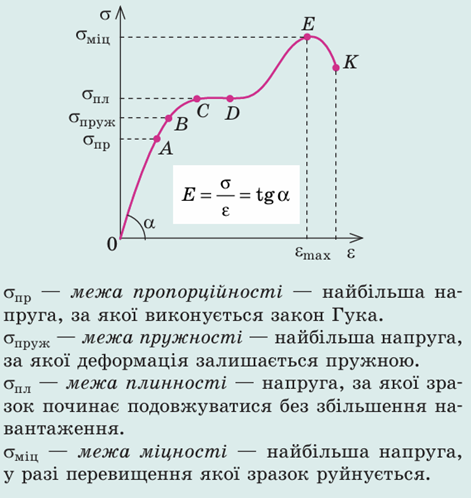
Досліди показують, що за невеликих деформацій (ділянка \(OA\) графіка) виконується закон Гука: у разі малих пружних деформацій розтягнення і стиснення механічна напруга \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}\) прямо пропорційна відносному видовженню \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}=E\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}. $$
Коефіцієнт пропорційності \(E\) ‒ це модуль Юнга або модуль пружності, який характеризує пружні властивості матеріалу. Одиниця модуля Юнга в SІ ‒ паскаль: $$ [E]=1\ \text{Па}\ (\text{Pa}). $$
З іншого боку, механічна напруга \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}\) ‒ це фізична величина, яка характеризує деформоване тіло і дорівнює відношенню модуля сили пружності \(F_\text{пруж}\) до площі \(S\) поперечного перерізу тіла: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}=\frac{F_\text{пруж}}{S}. $$
Можна прирівняти праві частини формул для механічної напруги і визначити з цієї рівності модуль Юнга:
\begin{gather*} E\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=\frac{F_\text{пруж}}{S},\\[6pt] E=\frac{F_\text{пруж}}{S\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}. \end{gather*}Гумова нитка перебуває в стані спокою після видовження, тому: \begin{gather*} F_\text{тяж}=F_\text{пруж},\\[7pt] F_\text{тяж}=mg, \end{gather*} де \(m\) ‒ маса підвішеного до гумової нитки тягарця, \(g\) ‒ прискорення вільного падіння $$ F_\text{пруж}=mg. $$
Відносне видовження \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\) тіла ‒ фізична величина, яка дорівнює відношенню видовження \(\Delta l\) (за умовою \(\Delta l=2\) см) до початкової довжини \(l_0\) (за умовою \(l_0=60\) см) тіла: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=\frac{\Delta l}{l_0}. $$
Підставмо у формулу для визначення модуля Юнга вирази для сили пружності й відносного видовження і обчислимо шукану величину:
Відповідь: \(20.\)
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного та паралельного з’єднання провідників, уміння визначати характеристики електричного струму.
Резистори \(1\) і \(2\) з’єднано паралельно, тому якщо додамо покази амперметрів, матимемо загальну силу струму в цьому електричному колі:
$$ I=I_1+I_2=0\mathord{,}6\ \text{А}+0\mathord{,}4\ \text{А}=1\ \text{А}. $$Це буде струм, який проходить крізь резистор \(3.\) Знаючи його опір, можемо за законом Ома для ділянки кола визначити, яку напругу подано на нього:
\begin{gather*} I=\frac{U_3}{R_3}\Rightarrow U_3=IR_3,\\[6pt] U_3=1\ \text{А}\cdot 2\ \text{Ом}=2\ \text{В}. \end{gather*}Відповідь: \(2.\)
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і розуміння побудови зображень, які дає тонка лінза, уміння застосовувати формулу тонкої лінзи й формулу для визначення лінійного збільшення лінзи.
Опишімо зазначене в умові розміщення предмета й лінзи формулою тонкої лінзи: $$ -\frac 1F=\frac 1d-\frac 1f, $$ де \(d\) ‒ відстань від предмета до лінзи (за умовою \(d=2F\) ‒ двом фокусним відстаням \(F\)), \(f\) ‒ відстань від лінзи до зображення.
Щодо знаків мінус у формулі: зауважмо, що відстань \(f\) (від лінзи до зображення) треба брати зі знаком мінус, якщо зображення є уявним (а розсіювальна лінза дає тільки уявні зображення), і зі знаком плюс, якщо зображення є дійсним; фокусна відстань \(F\) збиральної лінзи є додатною, а розсіювальної ‒ від’ємною.
Також скористаймося відношенням лінійного розміру \(H\) зображення предмета до розміру \(h\) самого предмета, яке називають лінійним збільшенням \(\text{Г}\) лінзи: $$ \text{Г}=\frac Hh=\frac{|f|}{|d|}. $$
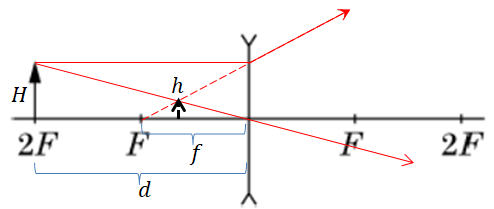
Виразімо висоту зображення \(H:\) $$ H=\frac{h|f|}{|d|}. $$
За умовою \(h=4\mathord{,}5\) см. За рисунком \(d=2F.\)
Відстань \(f\) від лінзи до зображення виразімо з формули тонкої лінзи:
\begin{gather*} -\frac 1F=\frac 1d-\frac 1f,\\[6pt] -\frac 1F=\frac{1}{2F}-\frac 1f,\\[6pt] \frac 1f=\frac{1}{2F}+\frac 1F=\frac{3}{2F},\\[6pt] f=\frac{2F}{3}. \end{gather*}Підставмо всі значення і вирази у формулу для \(H\) і визначмо шукану величину:
$$ H=\frac{h|f|}{|d|}=\frac{4\mathord{,}5\ \text{см}\cdot 2F}{3\cdot 2F}=1\mathord{,}5\ \text{см}. $$Відповідь: \(1\mathord{,}5.\)
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.
Завдання скеровано на перевірку знання і розуміння того, що кожне тіло має енергію просто внаслідок свого існування.
З погляду спеціальної теорії відносності, якщо тіло масою \(m\) рухається зі швидкістю \(v\) відносно якоїсь системи відліку, то енергія \(E\) тіла в цій системі відліку становить (\(c\) ‒ швидкість поширення світла у вакуумі): $$ E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}. $$
Будь-яке тіло (частинка), що має масу \(m\), несе із собою запас енергії. Навіть якщо швидкість руху тіла (частинки) зменшується до нуля \((v=0)\), то згідно з вище наведеною формулою тіло все одно має енергію \(E:\) \begin{gather*} E=mc^2. \end{gather*}
Зміна енергії \(\Delta E\) тіла прямо пропорційна зміні його маси \(\Delta m:\) $$ \Delta E=\Delta mc^2. $$
Передавання нерухомому тілу енергії завжди супроводжує збільшення його маси, і навпаки: виділення тілом енергії супроводжує зменшення його маси.
Отже, знаючи, на скільки зменшилася маса зорі внаслідок випромінювання, визначмо енергію випромінювання зорі:
Відповідь: \(360.\)
Знайшли помилку? Пишіть на